Навигация
Система лінійних однорідних алгебраїчних рівнянь. Фундаментальна сукупність розв'язків
Міністерство освіти і науки України
Закарпатський державний університет
ІНСТИТУТ ІНФОРМАТИКИ
КАФЕДРА ФІЗИКО-МАТЕМАТИЧНИХ ДИСЦИПЛІН
Реєстраційний №____
Дата ______________
КУРСОВА РОБОТА
з вищої математики
Тема: Система лінійних однорідних алгебраїчних рівнянь. Фундаментальна сукупність розв'язків.
Рекомендовано до захисту
“__” ____________ 2006 р.
Робота захищена
“__” ____________ 2006 р.
з оцінкою
__________
Підписи членів комісії:
студента II курсу
денного відділення
П. І. Б.
Науковий керівник
проф. П. І. Б.
Ужгород
Зміст
I. Вступ ______________________________________________________3
II. Теоретичний виклад матеріалу _________________________________4
1. Сумісність лінійних алгебраїчних рівнянь _____________________4
2. Ранг матриці ______________________________________________5
3. Фундаментальна система розв’язків __________________________7
4. Приклади розв’язання завдань _______________________________9
III. Висновок __________________________________________________14
Використана література ______________________________________15
Вступ
Спочатку нам потрібно розглянути те, як виглядають системи лінійних однорідних алгебраїчних рівнянь, ознайомитися з тими компонентами, які входять у ці системи.
Отже, система m лінійних алгебраїчних рівнянь з n невідомими в загальному випадку має вигляд:
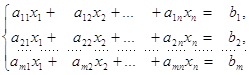
(2.1)
Тут n і m — довільні натуральні числа, ніяк не пов'язані між собою; x1, x2,…,xn — невідомі величини; ![]()
![]() (коефіцієнти системи),
(коефіцієнти системи), ![]() (вільні члени) — довільні відомі числа.
(вільні члени) — довільні відомі числа.
В цій роботі нас цікавитиме система, у якої всі вільні члени дорівнюють нулю. Тобто однорідна система до системи (2.1), яка має такий вигляд:
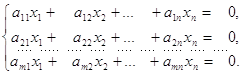
![]()
(2.2)
Вона буде називається однорідною системою, відповідною до системи (2.1).
Система ж (2.1) називається неоднорідною, якщо ![]() (принаймні одне з чисел
(принаймні одне з чисел ![]() є відмінним від нуля).
є відмінним від нуля).
Розв'язком системи (2.1) (системи (2.2)) називається така впорядкована система n чисел ![]() яка при підставленні в систему (2.1) (систему (2.2)) на місце невідомих
яка при підставленні в систему (2.1) (систему (2.2)) на місце невідомих ![]() відповідно, тобто замість
відповідно, тобто замість ![]() , підставляємо
, підставляємо ![]() , замість
, замість ![]() , підставляємо
, підставляємо ![]() і т. д., перетворює всі рівняння системи (2.1) (системи (2.2)) в правильні рівності. Розв'язок
і т. д., перетворює всі рівняння системи (2.1) (системи (2.2)) в правильні рівності. Розв'язок ![]() записують у вигляді n- вимірного вектора
записують у вигляді n- вимірного вектора ![]() .
.
Теоретичний виклад матеріалу
5. Сумісність лінійних алгебраїчних рівнянь.
Будь-яка система рівнянь називається сумісною, якщо вона має принаймні один розв'язок, і — несумісною, якщо вона не має жодного розв'язку. При цьому сумісна система називається визначеною, якщо вона має тільки один розв'язок, і — невизначеною, якщо вона має більше, ніж один розв'язок.
Дві системи рівнянь називаються еквівалентними, якщо обидві вони несумісні, або якщо обидві вони сумісні та мають одні й ті ж розв'язки. Системи лінійних алгебраїчних рівнянь є еквівалентними, якщо вони одержуються одна з однієї шляхом застосування скінченної послідовності таких перетворень.
• переставляння місцями двох рівнянь системи (елементарне перетворення першого роду),
• додавання до якогось рівняння системи іншого рівняння цієї системи, помноженого на деяке число (елементарне перетворення другого роду).
Кожній системі лінійних алгебраїчних рівнянь (2 1) чи (2.2) відповідає деяка матриця
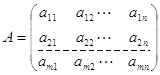 (2.3)
(2.3)
її називають матрицею цієї системи. Для системи (2.1) можна виписати матрицю
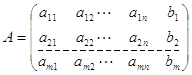 (2.4)
(2.4)
Її називають розширеною матрицею системи (2.1).
З іншого боку, кожну ![]() - матрицю можна розуміти як матрицю деякої системи m лінійних алгебраїчних рівнянь з n невідомими, а
- матрицю можна розуміти як матрицю деякої системи m лінійних алгебраїчних рівнянь з n невідомими, а ![]() - матрицю як розширену матрицю деякої неоднорідної системи m лінійних алгебраїчних рівнянь з n невідомими. Останнє зауваження означає, що система m лінійних алгебраїчних рівнянь з n невідомими з точністю до позначень невідомих, задається своєю розширеною
- матрицю як розширену матрицю деякої неоднорідної системи m лінійних алгебраїчних рівнянь з n невідомими. Останнє зауваження означає, що система m лінійних алгебраїчних рівнянь з n невідомими з точністю до позначень невідомих, задається своєю розширеною ![]() - матрицею.
- матрицею.
Неважко помітити, що, проводячи елементарні перетворення першого і другого роду в системі лінійних алгебраїчних рівнянь, ми маємо справу лише з коефіцієнтами при невідомих. Через це значно простіше виконувати елементарні перетворення, оперуючи не з самою системою, а лише з її розширеною матрицею. Таким чином, елементарні перетворення першого і другого роду над системами лінійних алгебраїчних рівнянь з невідомими здійснюються, як перетворення відповідних їм матриць. При цьому переставлянню місцями двох рівнянь системи відповідає переставляння місцями двох рядків матриці системи (елементарне перетворення першого роду), а додаванню до якогось рівняння системи іншого рівняння цієї системи, помноженого на деяке число, відповідає додавання до якогось рядка матриці системи іншого її рядка, помноженого на деяке число (елементарне перетворення другого роду).
Похожие работы
... ’язок де С1, С2 - довільні сталі. Загальний розв’язок системи лінійних алгебраїчних рівнянь подається не в одному й тому самому вигляді. 2. Метод Гауса Метод Гауса розв’язування системи лінійних алгебраїчних рівнянь полягає в послідовному виключенні змінних і перетворенні системи рівнянь (1) до трикутного вигляду (2) Припустимо, що в системі (1) коефіцієнт . Якщо ця ...
... кта та алгоритму його функціонування, або алгоритму процесу, а також уявлення опису на різноманітних мовах здійснюється взаємодією людини і ЕОМ. Система автоматизованого проектування - це комплеск засобів автоматизації проектування, взаємозв’язаних з необхідними підрозділами проектної організації або колективом спеціалістів (користувачем системи), які виконують автоматизоване проектування. САПР ...
... нтуватися на використання підручників [53; 54; 5]. У класах фізико-математичного спрямування доцільно орієнтуватись на використання підручників [53; 54; 5; 1]. РОЗДІЛ 2 ОСОБЛИВОСТІ ВИВЧЕННЯ МАТЕМАТИКИ У ПРОФІЛЬНИХ КЛАСАХ В СУЧАСНИХ УМОВАХ 2.1. ОСНОВНІ ПОЛОЖЕННЯ ПРОФІЛЬНОЇ ДИФЕРЕНЦІАЦІЇ НАВЧАННЯ МАТЕМАТИКИ Математика є універсальною мовою, яка широко застосовується в усіх ...
... Философия культуры. – М.: NOTA BENE, 2001. – 349 с. 5. Додельцев Р.Ф. Концепция культуры З. Фрейда. – М.: Знание, 1989. – 60 с. 6. Киссель М.А. Джамбаттиста Вико. – М.: Мысль, 1980. – 197 с. 7. Культурологія. Українська та зарубіжна культура: Навч. посібник (М.М.Закович, І.А.Зязюн, О.М.Семашко та ін.). – з вид. – К.: Знання, 2007. – 567 с. 8. Фрейд Зігмунд. Вступ до психоаналізу: Лекції ...
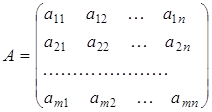
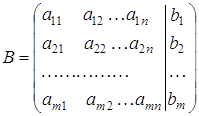
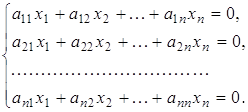
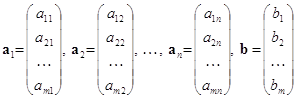




0 комментариев