Навигация
6. Ранг матриці.
Нехай ![]() – система таких n-вимірних векторів, що:
– система таких n-вимірних векторів, що:
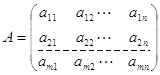 ,
,
тобто ![]() — система векторів-рядків матриці А. Цю систему можна впорядковувати різними способами.
— система векторів-рядків матриці А. Цю систему можна впорядковувати різними способами.
Нехай ![]() — певним чином впорядкована система векторів-рядків матриці А. Вилучаючи з цієї системи ті вектори-рядки матриці А, які лінійно виражаються через попередні, одержуємо лінійно незалежну підсистему
— певним чином впорядкована система векторів-рядків матриці А. Вилучаючи з цієї системи ті вектори-рядки матриці А, які лінійно виражаються через попередні, одержуємо лінійно незалежну підсистему ![]() векторів-рядків матриці А.
векторів-рядків матриці А.
Зрозуміло, що впорядковуючи різними способами систему векторів-рядків матриці А, ми будемо одержувати, загалом, різні лінійно незалежні підсистеми лінійно незалежних векторів-рядків матриці А. Спільним для всіх таких підсистем є кількість векторів-рядків матриці А, що входять до них. Власне, це число називається рангом системи векторів-рядків матриці А.
Означення. Рангом матриці А називається ранг системи її векторів-рядків.
Нехай А — довільна прямокутна ![]() матриця, k — таке натуральне число, що
матриця, k — таке натуральне число, що ![]() Зафіксуємо в цій матриці k рядків і k стовпців. Не змінюючи взаємного розташування елементів матриці А, розташованих на перетині зафіксованих рядків і стовпців, складемо з них матрицю k-го порядку. Детермінант цієї матриці називається мінором k-го порядку матриці А.
Зафіксуємо в цій матриці k рядків і k стовпців. Не змінюючи взаємного розташування елементів матриці А, розташованих на перетині зафіксованих рядків і стовпців, складемо з них матрицю k-го порядку. Детермінант цієї матриці називається мінором k-го порядку матриці А.
Кажуть, що мінор r+1-го порядку матриці А обводить мінор 1-го порядку, якщо він містить його в собі повністю.
Теорема. Найвищий порядок r відмінних від нуля мінорів матриці А дорівнює рангу цієї матриці.
Наслідок 1. Ранг системи векторів-рядків матриці А дорівнює рангові системи векторів-стовпців цієї матриці.
Наслідок 2. Детермінант квадратної матриці дорівнює нулю тоді і тільки тоді, коли якийсь її рядок є лінійною комбінацією інших її рядків.
Для знаходження рангу матриці А розмірності ![]() використовують такий алгоритм:
використовують такий алгоритм:
1) Якщо всі елементи матриці А дорівнюють нулю, тобто
![]()
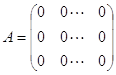 , то її ранг R(A) дорівнює нулю.
, то її ранг R(A) дорівнює нулю.
2) Якщо хоча би один елемент матриці А відмінний від нуля, то ![]() При цьому, якщо всі мінори другого порядку
При цьому, якщо всі мінори другого порядку
матриці дорівнюють нулю, то ![]() .
.
3) Якщо хоча би один мінор другого порядку матриці А відмінний від нуля, то ![]() При цьому, якщо всі мінори третього порядку
При цьому, якщо всі мінори третього порядку
матриці А, які обводять відмінний від нуля мінор другого порядку матриці A, дорівнюють нулю, то ![]() .
.
4) Якщо хоча би один мінор третього порядку матриці А відмінний від нуля, то ![]() При цьому, якщо всі мінори четвертого порядку матриці А, які обводять відмінний від нуля мінор третього порядку матриці А, дорівнюють нулю, то
При цьому, якщо всі мінори четвертого порядку матриці А, які обводять відмінний від нуля мінор третього порядку матриці А, дорівнюють нулю, то ![]() ... і т.д.
... і т.д.
Означення. Нехай r — ранг матриці ![]() . Будь-який відмінний від нуля мінор 1-го порядку матриці
. Будь-який відмінний від нуля мінор 1-го порядку матриці ![]() називають її базовим мінором.
називають її базовим мінором.
7. Фундаментальна система розв’язків.
З теореми Кронекера-Капеллі випливає, що будь-яка система (2.2) лінійних однорідних рівнянь є сумісною. Вона має очевидний (тривіальний) розв'язок: ![]() (його записують у вигляді (0.....0)). Якщо ранг матриці системи (2.2) дорівнює кількості невідомих, тобто
(його записують у вигляді (0.....0)). Якщо ранг матриці системи (2.2) дорівнює кількості невідомих, тобто ![]() , то така система має тільки нульовий розв'язок. Якщо ж
, то така система має тільки нульовий розв'язок. Якщо ж ![]() , де
, де ![]() , то в системі є n-r вільних невідомих, які можна дібрати так, щоб система (2.2) мала ще й ненульові розв'язки. Зазначимо, що система n лінійних однорідних рівнянь з n невідомими тоді і тільки тоді має розв'язки, відмінних від нульового, коли детермінант цієї системи дорівнює нулю.
, то в системі є n-r вільних невідомих, які можна дібрати так, щоб система (2.2) мала ще й ненульові розв'язки. Зазначимо, що система n лінійних однорідних рівнянь з n невідомими тоді і тільки тоді має розв'язки, відмінних від нульового, коли детермінант цієї системи дорівнює нулю.
Нехай вектори ![]() та є розв'язками с
та є розв'язками с![]() системи (2.2). Тоді при будь-якому дійсному k вектор
системи (2.2). Тоді при будь-якому дійсному k вектор ![]() також є розв'язком системи (2.2). Крім того, при будь-яких дійсних k та l вектор
також є розв'язком системи (2.2). Крім того, при будь-яких дійсних k та l вектор ![]() також є розв'язком системи (2.2). Іншими словами: будь-яка лінійна комбінація розв'язків системи (2.2) лінійних однорідних алгебраїчних рівнянь є розв'язком цієї ж системи Сукупність усіх можливих розв'язків системи (2.2) називають простором розв'язків цієї системи.
також є розв'язком системи (2.2). Іншими словами: будь-яка лінійна комбінація розв'язків системи (2.2) лінійних однорідних алгебраїчних рівнянь є розв'язком цієї ж системи Сукупність усіх можливих розв'язків системи (2.2) називають простором розв'язків цієї системи.
Систему (2.2) розв'язують за тим же алгоритмом, що й систему (2.1). При цьому, очевидно ![]() і ми фіксуємо деякий базовий мінор матриці А системи (2.2). Потім виконуємо такі дії:
і ми фіксуємо деякий базовий мінор матриці А системи (2.2). Потім виконуємо такі дії:
1. Відкидаємо всі ті рівняння системи (2.2), коефіцієнти при невідомих у яких не складають рядок вибраного базового мінора матриці А, тобто залишаємо тільки ![]() рівнянь системи (2.2).
рівнянь системи (2.2).
2. Всі невідомі в залишених нами рівняннях, коефіцієнти при яких не входять в базовий мінор, переносимо в праву частину рівняння (ці невідомі називають вільними).
3. Надаючи вільним невідомим довільних значень, знаходимо значення інших r невідомих (ці невідомі називаються головними).
Одержавши всі можливі розв'язки системи (2.2), ми можемо вибрати з них лінійно незалежні розв'язки. Для цього потрібно вільним невідомим (а їх є n-r, де ![]() ), наприклад,
), наприклад, ![]() надавати такі сукупності значень
надавати такі сукупності значень ![]() (i=1,...), щоб ці n-r-вимірні вектори виявилися лінійно незалежними. Таких векторів можна вибрати n-r. Для кожного з цих лінійно незалежних n-r-вимірних векторів, компонентами яких є значення вільних невідомих, знаходимо відповідні значення головних невідомих
(i=1,...), щоб ці n-r-вимірні вектори виявилися лінійно незалежними. Таких векторів можна вибрати n-r. Для кожного з цих лінійно незалежних n-r-вимірних векторів, компонентами яких є значення вільних невідомих, знаходимо відповідні значення головних невідомих ![]() , де (i=1,...,n-r). Тоді n-вимірні вектори
, де (i=1,...,n-r). Тоді n-вимірні вектори ![]() (i=1,...,n-r) є лінійно незалежними розв'язками системи (2.2). Таку систему розв'язків системи (2.2) лінійних однорідних рівнянь називають лінійно незалежною.
(i=1,...,n-r) є лінійно незалежними розв'язками системи (2.2). Таку систему розв'язків системи (2.2) лінійних однорідних рівнянь називають лінійно незалежною.
Зрозуміло, що лінійно незалежна система розв'язків системи (2.2) знаходиться неоднозначно. Це пов'язано з тим, що базовий мінор матриці системи (2.2) знаходиться неоднозначно, а, потім, довільним чином добираються лінійно незалежні рядки ![]() значень вільних невідомих. Будь-яка лінійно незалежна система розв'язків системи (2.2) лінійних однорідних рівнянь називається її фундаментальною системою .
значень вільних невідомих. Будь-яка лінійно незалежна система розв'язків системи (2.2) лінійних однорідних рівнянь називається її фундаментальною системою .
Якщо вже вибрана деяка фундаментальна система розв'язків системи (2.2), наприклад ![]() , то будь-який розв'язок
, то будь-який розв'язок ![]() цієї системи є лінійною комбінацією розв'язків фундаментальної системи, тобто
цієї системи є лінійною комбінацією розв'язків фундаментальної системи, тобто ![]() , і навпаки, будь-яка лінійна комбінація розв’язків фундаментальної системи є розв'язком системи (2.2). Якщо коефіцієнти
, і навпаки, будь-яка лінійна комбінація розв’язків фундаментальної системи є розв'язком системи (2.2). Якщо коефіцієнти ![]() цієї лінійної комбінації вважати довільними, то вона (тобто, ця лінійна комбінація) називається загальним розв'язком системи (2.2).
цієї лінійної комбінації вважати довільними, то вона (тобто, ця лінійна комбінація) називається загальним розв'язком системи (2.2).
Серед фундаментальних систем розв'язків системи (2.2) виділяють нормальну фундаментальну систему, яка відповідає таким лінійно незалежним n-r-вимірним векторам значень вільних невідомих (1,0,...,0), (0,1,…,0),...,(0,0,...,1) (тут кожний з n-r-векторів є n-r-вимірним).
Нехай (2.1) — довільна неоднорідна система лінійних алгебраїчних рівнянь, (2.2) — відповідна їй однорідна система. Якщо вектор ![]() —довільний розв'язок системи (2.1), а
—довільний розв'язок системи (2.1), а ![]() — довільний розв'язок системи (2.2), то
— довільний розв'язок системи (2.2), то ![]() є знову ж таки розв'язком неоднорідної системи лінійних рівнянь (2.1). Будь-який розв'язок лінійної неоднорідної системи (2.1) дорівнює сумі деякого розв’язку цієї системи і загального розв'язку відповідної їй однорідної системи (2.2). Такий розв'язок системи (2.1) називають її загальним розв’язком.
є знову ж таки розв'язком неоднорідної системи лінійних рівнянь (2.1). Будь-який розв'язок лінійної неоднорідної системи (2.1) дорівнює сумі деякого розв’язку цієї системи і загального розв'язку відповідної їй однорідної системи (2.2). Такий розв'язок системи (2.1) називають її загальним розв’язком.
Зауважимо також, що різниця двох розв'язків системи (2.1) є розв’язком системи (2.2).
Похожие работы
... ’язок де С1, С2 - довільні сталі. Загальний розв’язок системи лінійних алгебраїчних рівнянь подається не в одному й тому самому вигляді. 2. Метод Гауса Метод Гауса розв’язування системи лінійних алгебраїчних рівнянь полягає в послідовному виключенні змінних і перетворенні системи рівнянь (1) до трикутного вигляду (2) Припустимо, що в системі (1) коефіцієнт . Якщо ця ...
... кта та алгоритму його функціонування, або алгоритму процесу, а також уявлення опису на різноманітних мовах здійснюється взаємодією людини і ЕОМ. Система автоматизованого проектування - це комплеск засобів автоматизації проектування, взаємозв’язаних з необхідними підрозділами проектної організації або колективом спеціалістів (користувачем системи), які виконують автоматизоване проектування. САПР ...
... нтуватися на використання підручників [53; 54; 5]. У класах фізико-математичного спрямування доцільно орієнтуватись на використання підручників [53; 54; 5; 1]. РОЗДІЛ 2 ОСОБЛИВОСТІ ВИВЧЕННЯ МАТЕМАТИКИ У ПРОФІЛЬНИХ КЛАСАХ В СУЧАСНИХ УМОВАХ 2.1. ОСНОВНІ ПОЛОЖЕННЯ ПРОФІЛЬНОЇ ДИФЕРЕНЦІАЦІЇ НАВЧАННЯ МАТЕМАТИКИ Математика є універсальною мовою, яка широко застосовується в усіх ...
... Философия культуры. – М.: NOTA BENE, 2001. – 349 с. 5. Додельцев Р.Ф. Концепция культуры З. Фрейда. – М.: Знание, 1989. – 60 с. 6. Киссель М.А. Джамбаттиста Вико. – М.: Мысль, 1980. – 197 с. 7. Культурологія. Українська та зарубіжна культура: Навч. посібник (М.М.Закович, І.А.Зязюн, О.М.Семашко та ін.). – з вид. – К.: Знання, 2007. – 567 с. 8. Фрейд Зігмунд. Вступ до психоаналізу: Лекції ...
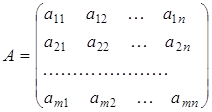
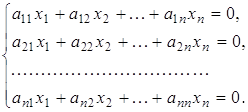
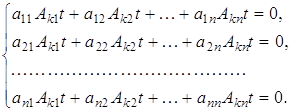
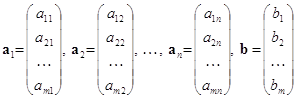




0 комментариев