Навигация
Приклади розв’язання завдань
17031
знак
2
таблицы
1
изображение
2. Приклади розв’язання завдань.
Завдання 1. Знайти фундаментальну систему розв'язків та загальний розв'язок системи лінійних однорідних рівнянь:
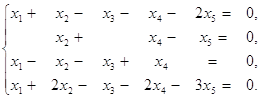
Розв'язання. Кожна система лінійних однорідних рівнянь є сумісною. Знаходимо ранг матриці А цієї системи.
А =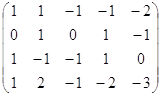 
Матриця А — ненульова, отже, 
Обчислюємо мінори третього порядку матриці А, одержані обведенням відмінного від нуля мінора 
другого порядку. Звернемо увагу на те, що третій і четвертий стовпці матриці А пропорційні відповідно першому та другому її стовпцям. Тому мінори, утворені обведенням за допомогою як третього, так і четвертого стовпців, дорівнюють нулю. Залишається обчислити ще два мінори, утворені обведенням за допомогою п'ятого стовпця.
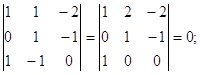
Таким чином, ранг матриці А дорівнює 2. Зважаючи на те, що її базовий мінор розташовано в лівому верхньому куті матриці А, залишаємо в системі тільки перші два рівняння, а в їх лівих частинах — тільки перші дві невідомі. Інші три невідомі переносимо в праві частини, тобто вільними невідомими є 
. Маємо:
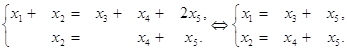
Складемо таблицю для невідомих x1, x2, x3, x4, x5, відокремивши в ній головні (x1 та x2) і вільні (х3, х4, та х5) невідомі. Надаємо вільним невідомим (х3, х4, х5) такі, наприклад, значення: (1, 0, 0) = 
1 , (0,1, 0) = 2 , (0, 0,1) = 3 (вибір значень для вільних невідомих зроблено так, щоб вектори 1, 2 та 3 виявилися лінійно незалежними). Більше лінійно незалежних тривимірних векторів вибрати не можна. Для кожного набору значень вільних невідомих знаходимо відповідні значення головних невідомих. Одержана таблиця має такий вигляд:
| x1 | х2 | х3 | х4 | х5 |
| х3+х5 | х4+х5 | х3 | х4 | х5 |
| 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
Другий рядок таблиці (х3+x5, х4+х5, x3, х4, х5) є загальним розв'язком розглядуваної системи, якщо х3, x4 та х5 є будь-які числа; третій — α1 = (1, 0, 1, 0, 0), четвертий — α2 = (0, 1, 0, 1, 0) та п'ятий — α3 = (1, 1, 0, 0, 1) є частинними розв'язками розглядуваної системи.
Останні рядки, тобто вектори α1, α2 та α3 є лінійно незалежними, бо і лінійно незалежними є їх частини, відповідно, 1, 2 та 3 . Вектори α1, α2 та α3 утворюють фундаментальну систему розв'язків розглядуваної нами в цьому завданні системи. Зауважимо, що ми здійснили такий вибір значень вільних невідомих, при якому одержано нормальну фундаментальну систему α1, α2 та α3 розв'язків заданої системи рівнянь.
Завдання 2. Знайти фундаментальну систему розв'язків.
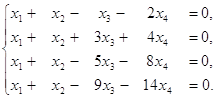
Розв'язання. Кожна система лінійних однорідних рівнянь є сумісною. Знаходимо ранг матриці А цієї системи.
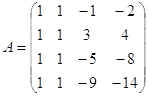
Матриця А — ненульова, отже, 
Обчислюємо мінори третього порядку матриці А, одержані обведенням відмінного від нуля мінора 
другого порядку. Бачимо, що перший і другий рядки однакові, тому нам досить обчислити два мінори третього порядку утворені обведенням першого стовпця і третього рядка, першого стовпця і четвертого рядка.
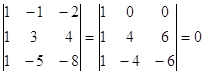, тому що другий і третій рядки пропорційні.
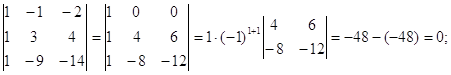
Таким чином, ранг матриці А дорівнює 2. Зважаючи на те, що її базовий мінор розташовано в правому верхньому куті матриці А, залишаємо в системі тільки перші два рівняння, а в їх лівих частинах — тільки ті невідомі, коефіцієнти при яких ввійшли до базового мінору. Інші дві невідомі переносимо в праві частини, тобто вільними невідомими є х3 та х4. Маємо:
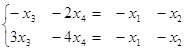
Додамо до другого рівняння перше помножене на 3
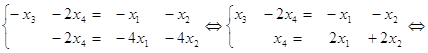
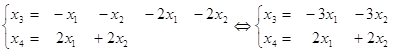
Складемо таблицю для невідомих x1, x2, x3, x4, відокремивши в ній головні (x3 та x4) і вільні (х1 та х2) невідомі. Надаємо вільним невідомим (х1 та х2) такі, наприклад, значення: (1, 0) = 1 , (0,1) = 2, (вибір значень для вільних невідомих зроблено так, щоб вектори 1 та 2 виявилися лінійно незалежними). Більше лінійно незалежних векторів вибрати не можна. Для кожного набору значень вільних невідомих знаходимо відповідні значення головних невідомих. Одержана таблиця має такий вигляд:
|
|
|
|
|
|
|
|
|
|
| 1 | 0 | -3 | 2 |
| 0 | 1 | -3 | 2 |
Другий рядок таблиці 
є загальним розв'язком розглядуваної системи, якщо х1 та х2 є будь-які числа; третій — α1 = (1, 0, -3, 2) та четвертий — α2 = (0, 1, -3, 2) є частинними розв'язками розглядуваної системи. Останні рядки, тобто вектори α1 та α2 є лінійно незалежними, бо і лінійно незалежними є їх частини, відповідно, 1 та 2 . Вектори α1 та α2 утворюють фундаментальну систему розв'язків розглядуваної нами в цьому завданні системи. Зауважимо, що ми здійснили такий вибір значень вільних невідомих, при якому одержано нормальну фундаментальну систему α1 та α2 розв'язків заданої системи рівнянь
Висновок
Можна визначити такий основний алгоритм знаходження фундаментальної системи розв’язків лінійних однорідних рівнянь:
1. Виписуємо матрицю системи, при цьому вибираємо один з мінорів, що відмінний від нуля найвищого порядку. Його назвемо базою мінор.
2. Тоді в розглядуваній СЛОР відкидаємо всі ті рівняння коефіцієнти при яких не увійшли до базового мінора.
3. В рівняннях, що залишилися переносимо у праву частину ті члени коефіцієнти при невідомих у яких не увійшли до базового мінора. Ці невідомі назвемо вільними невідомими. Ті ж невідомі, що залишилися у тій лівій частині назвемо – головними.
4. Виражаємо головні невідомі через вільні невідомі. Значення для вільних невідомих різними способами підбираємо так, що набори, які утворилися при цьому є лінійно незалежними.
5. Підставляючи ці значення у розв’язок для головних невідомих одержуємо фундаментальну систему розв’язків.
Використана література
1. Курош А. Г., “ Курс высшей алгебры ”, изд. 10, <<Наука>>, Москва, 1971 г., 432 стр.
2. Ф. Г. Ващук, С. С. Поляк, І. О. Пономарьова, “ Практикум з алгебри ”, Ужгород, 1997 р., 147ст.
3. Овчинников П. Ф., Яремчук Ф. П., Михайленко В. М.. Высшая математика – К.: Вища шк. Главное изд., 1987 г., 552 стр.
4. Ващук Ф. Г., Поляк С. С.. Практикум з вищої математики. Частина І: Елементи алгебри та аналітичної геометрії. – Ужгород: Гражда, 2005. – 294 с.: іл.
Похожие работы
... ’язок де С1, С2 - довільні сталі. Загальний розв’язок системи лінійних алгебраїчних рівнянь подається не в одному й тому самому вигляді. 2. Метод Гауса Метод Гауса розв’язування системи лінійних алгебраїчних рівнянь полягає в послідовному виключенні змінних і перетворенні системи рівнянь (1) до трикутного вигляду (2) Припустимо, що в системі (1) коефіцієнт . Якщо ця ...
... кта та алгоритму його функціонування, або алгоритму процесу, а також уявлення опису на різноманітних мовах здійснюється взаємодією людини і ЕОМ. Система автоматизованого проектування - це комплеск засобів автоматизації проектування, взаємозв’язаних з необхідними підрозділами проектної організації або колективом спеціалістів (користувачем системи), які виконують автоматизоване проектування. САПР ...
... нтуватися на використання підручників [53; 54; 5]. У класах фізико-математичного спрямування доцільно орієнтуватись на використання підручників [53; 54; 5; 1]. РОЗДІЛ 2 ОСОБЛИВОСТІ ВИВЧЕННЯ МАТЕМАТИКИ У ПРОФІЛЬНИХ КЛАСАХ В СУЧАСНИХ УМОВАХ 2.1. ОСНОВНІ ПОЛОЖЕННЯ ПРОФІЛЬНОЇ ДИФЕРЕНЦІАЦІЇ НАВЧАННЯ МАТЕМАТИКИ Математика є універсальною мовою, яка широко застосовується в усіх ...
... Философия культуры. – М.: NOTA BENE, 2001. – 349 с. 5. Додельцев Р.Ф. Концепция культуры З. Фрейда. – М.: Знание, 1989. – 60 с. 6. Киссель М.А. Джамбаттиста Вико. – М.: Мысль, 1980. – 197 с. 7. Культурологія. Українська та зарубіжна культура: Навч. посібник (М.М.Закович, І.А.Зязюн, О.М.Семашко та ін.). – з вид. – К.: Знання, 2007. – 567 с. 8. Фрейд Зігмунд. Вступ до психоаналізу: Лекції ...
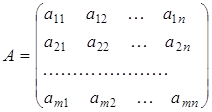
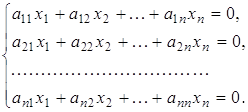
0 комментариев