Навигация
Задачи теории массового обслуживания
1.5 Задачи теории массового обслуживания
Примеры систем массового обслуживания (СМО): телефонные станции, ремонтные мастерские, билетные кассы, справочные бюро, станочные и другие технологические системы, системы управления гибких производственных систем и т.д.
Каждая СМО состоит из какого–то количества обслуживающих единиц, которые называются каналами обслуживания (это станки, транспортные тележки, роботы, линии связи, кассиры, продавцы и т.д.). Всякая СМО предназначена для обслуживания какого–то потока заявок (требований), поступающих в какие-то случайные моменты времени.
Обслуживание заявки продолжается какое–то, вообще говоря, случайное время, после чего канал освобождается и готов к приему следующей заявки. Случайный характер потока заявок и времени обслуживания приводит к тому, что в какие–то периоды времени на входе СМО скапливается излишне большое количество заявок (они либо становятся в очередь, либо покидают СМО не обслуженными). В другие же периоды СМО будет работать с недогрузкой или вообще простаивать.
Процесс работы СМО – случайный процесс с дискретными состояниями и непрерывным временем. Состояние СМО меняется скачком в моменты появления каких-то событий (прихода новой заявки, окончания обслуживания, момента, когда заявка, которой надоело ждать, покидает очередь).
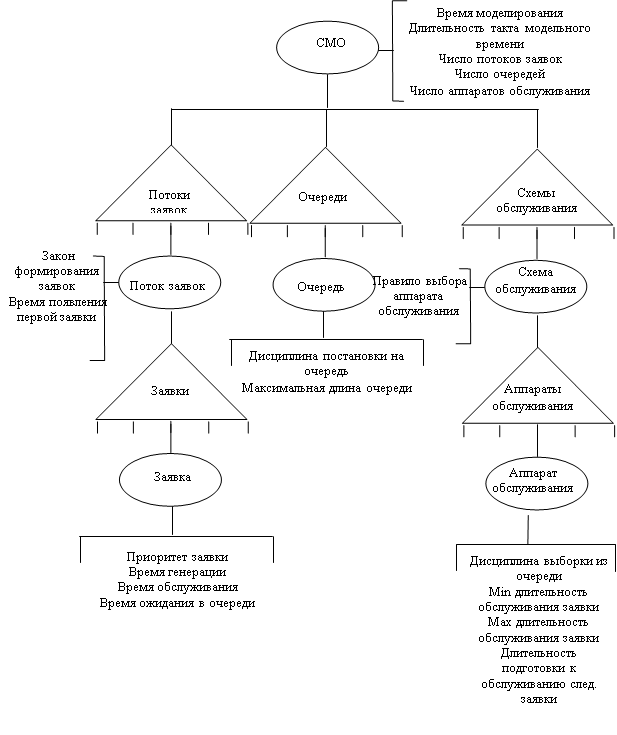
Предмет теории массового обслуживания – построение математических моделей, связывающих заданные условия работы СМО (число каналов, их производительность, правила работы, характер потока заявок) с интересующими нас характеристиками – показателями эффективности СМО. Эти показатели описывают способность СМО справляться с потоком заявок. Ими могут быть: среднее число заявок, обслуживаемых СМО в единицу времени; среднее число занятых каналов; среднее число заявок в очереди; среднее время ожидания обслуживания и т.д.
Математический анализ работы СМО очень облегчается, если процесс этой работы Марковский, т.е. потоки событий, переводящие систему из состояния в состояние – простейшие. Иначе математическое описание процесса очень усложняется и его редко удается довести до конкретных аналитических зависимостей. На практике не Марковские процессы с приближением приводятся к Марковским. Приведенный далее математический аппарат описывает Марковские процессы.
1.6 Классификация систем массового обслуживания
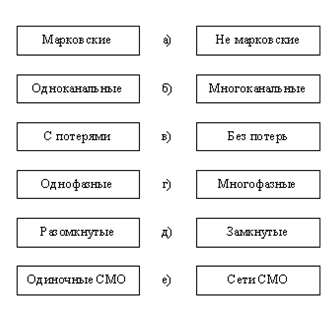
Первое деление (по наличию очередей):
1. СМО с отказами;
2. СМО с очередью.
В СМО с отказами заявка, поступившая в момент, когда все каналы заняты, получает отказ, покидает СМО и в дальнейшем не обслуживается.
В СМО с очередью заявка, пришедшая в момент, когда все каналы заняты, не уходит, а становится в очередь и ожидает возможности быть обслуженной.
СМО с очередями подразделяются на разные виды в зависимости от того, как организована очередь – ограничена или не ограничена. Ограничения могут касаться как длины очереди, так и времени ожидания, «дисциплины обслуживания».
Итак, например, рассматриваются следующие СМО:
· СМО с нетерпеливыми заявками (длина очереди и время обслуживания ограничено);
· СМО с обслуживанием с приоритетом, т.е. некоторые заявки обслуживаются вне очереди и т.д.
Кроме этого СМО делятся на открытые СМО и замкнутые СМО.
В открытой СМО характеристики потока заявок не зависят от того, в каком состоянии сама СМО (сколько каналов занято). В замкнутой СМО – зависят. Например, если один рабочий обслуживает группу станков, время от времени требующих наладки, то интенсивность потока «требований» со стороны станков зависит от того, сколько их уже исправно и ждет наладки.
Классификация СМО далеко не ограничивается приведенными разновидностями, но этого достаточно.
2. Системы массового обслуживания с ожиданием
2.1 Одноканальная СМО с ожиданием
Рассмотрим простейшую СМО с ожиданием — одноканальную систему (n - 1), в которую поступает поток заявок с интенсивностью ![]() ; интенсивность обслуживания
; интенсивность обслуживания ![]() (т.е. в среднем непрерывно занятый канал будет выдавать
(т.е. в среднем непрерывно занятый канал будет выдавать ![]() обслуженных заявок в единицу (времени). Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания.
обслуженных заявок в единицу (времени). Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания.
Система с ограниченной длиной очереди. Предположим сначала, что количество мест в очереди ограничено числом m, т.е. если заявка пришла в момент, когда в очереди уже стоят m-заявок, она покидает систему не обслуженной. В дальнейшем, устремив m к бесконечности, мы получим характеристики одноканальной СМО без ограничений длины очереди.
Будем нумеровать состояния СМО по числу заявок, находящихся в системе (как обслуживаемых, так и ожидающих обслуживания):
![]() — канал свободен;
— канал свободен;
![]() — канал занят, очереди нет;
— канал занят, очереди нет;
![]() — канал занят, одна заявка стоит в очереди;
— канал занят, одна заявка стоит в очереди;
![]() — канал занят, k-1 заявок стоят в очереди;
— канал занят, k-1 заявок стоят в очереди;
![]() — канал занят, т-заявок стоят в очереди.
— канал занят, т-заявок стоят в очереди.
ГСП показан на рис. 4. Все интенсивности потоков событий, переводящих в систему по стрелкам слева направо, равны ![]() , а справа налево —
, а справа налево — ![]() . Действительно, по стрелкам слева направо систему переводит поток заявок (как только придет заявка, система переходит в следующее состояние), справа же налево — поток «освобождений» занятого канала, имеющий интенсивность
. Действительно, по стрелкам слева направо систему переводит поток заявок (как только придет заявка, система переходит в следующее состояние), справа же налево — поток «освобождений» занятого канала, имеющий интенсивность ![]() (как только будет обслужена очередная заявка, канал либо освободится, либо уменьшится число заявок в очереди).
(как только будет обслужена очередная заявка, канал либо освободится, либо уменьшится число заявок в очереди).

Рис. 4. Одноканальная СМО с ожиданием
Изображенная на рис. 4 схема представляет собой схему размножения и гибели. Напишем выражения для предельных вероятностей состояний:
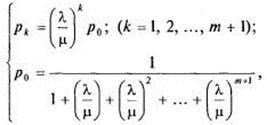 (5)
(5)
или с использованием: ![]() :
:
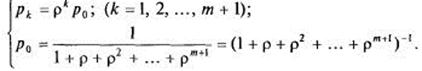 (6)
(6)
Последняя строка в (6) содержит геометрическую прогрессию с первым членом 1 и знаменателем р, откуда получаем:
![]() (7)
(7)
в связи с чем предельные вероятности принимают вид:
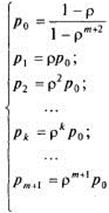 (8).
(8).
Выражение (7) справедливо только при ![]() < 1 (при
< 1 (при ![]() = 1 она дает неопределенность вида 0/0). Сумма геометрической прогрессии со знаменателем
= 1 она дает неопределенность вида 0/0). Сумма геометрической прогрессии со знаменателем ![]() = 1 равна m+2, и в этом случае:
= 1 равна m+2, и в этом случае:
![]() .
.
Определим характеристики СМО: вероятность отказа ![]() , относительную пропускную способность q, абсолютную пропускную способность А, среднюю длину очереди
, относительную пропускную способность q, абсолютную пропускную способность А, среднюю длину очереди ![]() , среднее число заявок, связанных с системой
, среднее число заявок, связанных с системой ![]() , среднее время ожидания в очереди
, среднее время ожидания в очереди ![]() , среднее время пребывания заявки в СМО
, среднее время пребывания заявки в СМО ![]() .
.
Вероятность отказа. Очевидно, заявка получает отказ только в случае, когда канал занят и все т-мест в очереди тоже:
![]() (9).
(9).
Относительная пропускная способность:
![]() (10).
(10).
Абсолютная пропускная способность:
![]() .
.
Средняя длина очереди. Найдем среднее число ![]() -заявок, находящихся в очереди, как математическое ожидание дискретной случайной величины R—числа заявок, находящихся в очереди:
-заявок, находящихся в очереди, как математическое ожидание дискретной случайной величины R—числа заявок, находящихся в очереди:
![]() .
.
С вероятностью![]() в очереди стоит одна заявка, с вероятностью
в очереди стоит одна заявка, с вероятностью![]() — две заявки, вообще с вероятностью
— две заявки, вообще с вероятностью![]() в очереди стоят k-1 заявок, и т.д., откуда:
в очереди стоят k-1 заявок, и т.д., откуда:
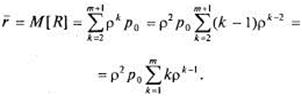 (11).
(11).
Поскольку ![]() , сумму в (11) можно трактовать как производную по
, сумму в (11) можно трактовать как производную по ![]() от суммы геометрической прогрессии:
от суммы геометрической прогрессии:
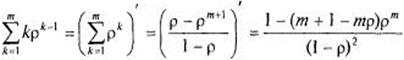 .
.
Подставляя данное выражение в (11) и используя ![]() из (8), окончательно получаем:
из (8), окончательно получаем:
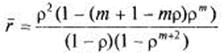 (12).
(12).
Среднее число заявок, находящихся в системе. Получим далее формулу для среднего числа ![]() -заявок, связанных с системой (как стоящих в очереди, так и находящихся на обслуживании). Поскольку
-заявок, связанных с системой (как стоящих в очереди, так и находящихся на обслуживании). Поскольку ![]() , где
, где ![]() — среднее число заявок, находящихся под обслуживанием, а k известно, то остается определить
— среднее число заявок, находящихся под обслуживанием, а k известно, то остается определить ![]() . Поскольку канал один, число обслуживаемых заявок может равняться 0 (с вероятностью
. Поскольку канал один, число обслуживаемых заявок может равняться 0 (с вероятностью ![]() ) или 1 (с вероятностью 1 -
) или 1 (с вероятностью 1 - ![]() ), откуда:
), откуда:
![]() .
.
и среднее число заявок, связанных с СМО, равно:
![]() (13).
(13).
Среднее время ожидания заявки в очереди. Обозначим его ![]() ; если заявка приходит в систему в какой-то момент времени, то с вероятностью
; если заявка приходит в систему в какой-то момент времени, то с вероятностью ![]() канал обслуживания не будет занят, и ей не придется стоять в очереди (время ожидания равно нулю). С вероятностью
канал обслуживания не будет занят, и ей не придется стоять в очереди (время ожидания равно нулю). С вероятностью ![]() она придет в систему во время обслуживания какой-то заявки, но перед ней не будет очереди, и заявка будет ждать начала своего обслуживания в течение времени
она придет в систему во время обслуживания какой-то заявки, но перед ней не будет очереди, и заявка будет ждать начала своего обслуживания в течение времени ![]() (среднее время обслуживания одной заявки). С вероятностью
(среднее время обслуживания одной заявки). С вероятностью ![]() в очереди перед рассматриваемой заявкой будет стоять еще одна, и время ожидания в среднем будет равно
в очереди перед рассматриваемой заявкой будет стоять еще одна, и время ожидания в среднем будет равно ![]() , и т.д.
, и т.д.
Если же k=m+1, т.е. когда вновь приходящая заявка застает канал обслуживания занятым и m-заявок в очереди (вероятность этого ![]() ), то в этом случае заявка не становится в очередь (и не обслуживается), поэтому время ожидания равно нулю. Среднее время ожидания будет равно:
), то в этом случае заявка не становится в очередь (и не обслуживается), поэтому время ожидания равно нулю. Среднее время ожидания будет равно:
![]() ,
,
если подставить сюда выражения для вероятностей (8), получим:
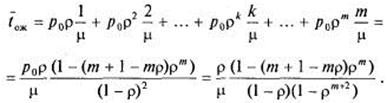 (14).
(14).
Здесь использованы соотношения (11), (12) (производная геометрической прогрессии), а также ![]() из (8). Сравнивая это выражение с (12), замечаем, что иначе говоря, среднее время ожидания равно среднему числу заявок в очереди, деленному на интенсивность потока заявок.
из (8). Сравнивая это выражение с (12), замечаем, что иначе говоря, среднее время ожидания равно среднему числу заявок в очереди, деленному на интенсивность потока заявок.
![]() (15).
(15).
Среднее время пребывания заявки в системе. Обозначим ![]() - матожидание случайной величины — время пребывания заявки в СМО, которое складывается из среднего времени ожидания в очереди
- матожидание случайной величины — время пребывания заявки в СМО, которое складывается из среднего времени ожидания в очереди ![]() и среднего времени обслуживания
и среднего времени обслуживания ![]() . Если загрузка системы составляет 100%, очевидно,
. Если загрузка системы составляет 100%, очевидно, ![]() , в противном же случае:
, в противном же случае:
![]() .
.
Отсюда:
![]() .
.
Пример 1. Автозаправочная станция (АЗС) представляет собой СМО с одним каналом обслуживания (одной колонкой).
Площадка при станции допускает пребывание в очереди на заправку не более трех машин одновременно (m = 3). Если в очереди уже находятся три машины, очередная машина, прибывшая к станции, в очередь не становится. Поток машин, прибывающих для заправки, имеет интенсивность ![]() =1 (машина в минуту). Процесс заправки продолжается в среднем 1,25 мин.
=1 (машина в минуту). Процесс заправки продолжается в среднем 1,25 мин.
Определить:
вероятность отказа;
относительную и абсолютную пропускную способности АЗС;
среднее число машин, ожидающих заправки;
среднее число машин, находящихся на АЗС (включая обслуживаемую);
среднее время ожидания машины в очереди;
среднее время пребывания машины на АЗС (включая обслуживание).
Иначе говоря, среднее время ожидания равно среднему числу заявок в очереди, деленному на интенсивность потока заявок.
Находим вначале приведенную интенсивность потока заявок: ![]() =1/1,25=0,8;
=1/1,25=0,8; ![]() =1/0,8=1,25.
=1/0,8=1,25.
По формулам (8):
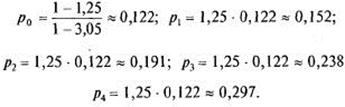
Вероятность отказа ![]() 0,297.
0,297.
Относительная пропускная способность СМО: q=1-![]() =0,703.
=0,703.
Абсолютная пропускная способность СМО: A=![]() =0,703 машины в мин.
=0,703 машины в мин.
Среднее число машин в очереди находим по формуле (12):
![]() ,
,
т.е. среднее число машин, ожидающих в очереди на заправку, равно 1,56.
Прибавляя к этой величине среднее число машин, находящихся под обслуживанием:
![]()
получаем среднее число машин, связанных с АЗС.
Среднее время ожидания машины в очереди по формуле (15):
![]()
Прибавляя к этой величине ![]() , получим среднее время, которое машина проводит на АЗС:
, получим среднее время, которое машина проводит на АЗС:
![]()
Системы с неограниченным ожиданием. В таких системах значение т не ограничено и, следовательно, основные характеристики могут быть получены путем предельного перехода ![]() в ранее полученных выражениях (5), (6) и т.п.
в ранее полученных выражениях (5), (6) и т.п.
Заметим, что при этом знаменатель в последней формуле (6) представляет собой сумму бесконечного числа членов геометрической прогрессии. Эта сумма сходится, когда прогрессия бесконечно убывающая, т.е. при ![]() <1.
<1.
Может быть доказано, что ![]() <1 есть условие, при котором в СМО с ожиданием существует предельный установившийся режим, иначе такого режима не существует, и очередь при
<1 есть условие, при котором в СМО с ожиданием существует предельный установившийся режим, иначе такого режима не существует, и очередь при ![]() будет неограниченно возрастать. Поэтому в дальнейшем здесь предполагается, что
будет неограниченно возрастать. Поэтому в дальнейшем здесь предполагается, что ![]() <1.
<1.
Если![]() , то соотношения (8) принимают вид:
, то соотношения (8) принимают вид:
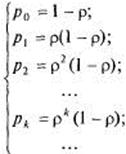 (16).
(16).
При отсутствии ограничений по длине очереди каждая заявка, пришедшая в систему, будет обслужена, поэтому q=1, ![]() .
.
Среднее число заявок в очереди получим из (12) при ![]() :
:
![]() .
.
Среднее число заявок в системе по формуле (13) при ![]() :
:
![]() .
.
Среднее время ожидания![]() получим из формулы (14) при
получим из формулы (14) при![]() :
:
![]() .
.
Наконец, среднее время пребывания заявки в СМО есть:
![]() .
.
Похожие работы
... и эффективным средством выработки оптимальных управленческий решений, главной особенностью которых в современных условиях становится их своевременность. 2 Применение теории массового обслуживания в экономическом анализе 2.1 Теория массового обслуживания Теория массового обслуживания – вероятностные модели реальных систем обслуживания населения, при которых время обслуживания будет ...
... остальных состояний системы. В результате получим систему уравнений: Решение этой системы будет иметь вид: (4) , ,…, (5) 4. Основные понятия и классификация систем массового обслуживания Заявкой (или требованием) называется спрос на удовлетворение какой-либо потребности (далее потребности предполагаются однотипными). Выполнение ...
... 2-3 Поиск литературы 7 1 7 2-4 Разработка модели разветвленной СМО 6 1 6 3 Поиск литературы завершен 3-6 Изучение литературы по теории массового обслуживания 10 1 10 4 Модель разработана 4-5 Разработка алгоритма программы 10 1 10 5 Алгоритм программы разработан 5-7 Выбор среды программиро-вания и создание программы 30 1 ...
... очередь длины k, остается в ней с вероятностью Pk и не присоединяется к очереди с вероятностью gk=1 - Pk,'. именно так обычно ведут себя люди в очередях. В системах массового обслуживания, являющихся математическими моделями производственных процессов, возможная длина очереди ограничена постоянной величиной (емкость бункера, например). Очевидно, это частный случай общей постановки. Некоторые ...
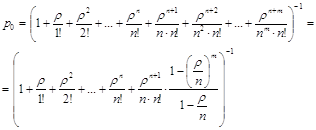

0 комментариев