Навигация
3. Замкнутые СМО
До сих пор мы рассматривали системы, в которых входящий поток никак не связан с выходящим. Такие системы называются разомкнутыми. В некоторых же случаях обслуженные требования после задержки опять поступают на вход. Такие СМО называются замкнутыми. Поликлиника, обслуживающая данную территорию, бригада рабочих, закрепленная за группой станков, являются примерами замкнутых систем.
В замкнутой СМО циркулирует одно и то же конечное число потенциальных требований. Пока потенциальное требование не реализовалось в качестве требования на обслуживание, считается, что оно находится в блоке задержки. В момент реализации оно поступает в саму систему. Например, рабочие обслуживают группу станков. Каждый станок является потенциальным требованием, превращаясь в реальное в момент своей поломки. Пока станок работает, он находится в блоке задержки, а с момента поломки до момента окончания ремонта - в самой системе. Каждый рабочий является каналом обслуживания.
Пусть n - число каналов обслуживания, s - число потенциальных заявок, n<s, ![]() - интенсивность потока заявок каждого потенциального требования, μ - интенсивность обслуживания:
- интенсивность потока заявок каждого потенциального требования, μ - интенсивность обслуживания:
ρ=![]() .
.
Вероятность простоя системы определяется формулой
Р0=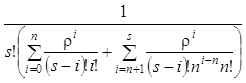 .
.
Финальные вероятности состояний системы:
Pk=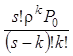 при k<n, Pk=
при k<n, Pk= при
при ![]() .
.
Через эти вероятности выражается среднее число занятых каналов
![]() =P1+2P2+…+n(Pn+Pn+1+…+Ps) или
=P1+2P2+…+n(Pn+Pn+1+…+Ps) или
![]() =P1+2P2+…+(n-1)Pn-1+n(1-P0-P1-…-Pn-1).
=P1+2P2+…+(n-1)Pn-1+n(1-P0-P1-…-Pn-1).
Через ![]() находим абсолютную пропускную способность системы:
находим абсолютную пропускную способность системы:
A=![]()
![]() ,
,
а также среднее число заявок в системе
М=s-![]() =s-
=s-![]() .
.
Пример 1. На вход трехканальной СМО с отказами поступает поток заявок с интенсивностью ![]() =4 заявки в минуту, время обслуживания заявки одним каналом tобсл=1/μ =0,5 мин. Выгодно ли с точки зрения пропускной способности СМО заставить все три канала обслуживать заявки сразу, причем среднее время обслуживания уменьшается втрое? Как это скажется на среднем времени пребывания заявки в СМО?
=4 заявки в минуту, время обслуживания заявки одним каналом tобсл=1/μ =0,5 мин. Выгодно ли с точки зрения пропускной способности СМО заставить все три канала обслуживать заявки сразу, причем среднее время обслуживания уменьшается втрое? Как это скажется на среднем времени пребывания заявки в СМО?
Решение. Находим вероятность простоя трехканальной СМО по формуле

ρ =![]() /μ =4/2=2, n=3,
/μ =4/2=2, n=3,
Р0= =
=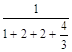 =
=![]()
![]() 0,158.
0,158.
Вероятность отказа определяем по формуле:
Ротк=Рn=![]() =
= ![]()
Pотк=![]()
![]() 0,21.
0,21.
Относительная пропускная способность системы:
Робсл=1-Ротк![]() 1-0,21=0,79.
1-0,21=0,79.
Абсолютная пропускная способность системы:
А=![]() Робсл
Робсл![]() 3,16.
3,16.
Среднее число занятых каналов определяем по формуле:
![]()
![]()
![]() 1,58, доля каналов, занятых обслуживанием,
1,58, доля каналов, занятых обслуживанием,
![]()
q=![]()
![]() 0,53.
0,53.
Cреднее время пребывания заявки в СМО находим как вероятность того, что заявка принимается к обслуживанию, умноженную на среднее время обслуживания: tСМО![]() 0,395 мин.
0,395 мин.
Объединяя все три канала в один, получаем одноканальную систему с параметрами μ=6, ρ=2/3. Для одноканальной системы вероятность простоя:
Р0=![]() =
=![]() =0,6,
=0,6,
вероятность отказа:
Ротк=ρ Р0=![]() =0,4,
=0,4,
относительная пропускная способность:
Робсл=1-Ротк=0,6,
абсолютная пропускная способность:
А=![]() Робсл=2,4.
Робсл=2,4.
Среднее время пребывания заявки в СМО:
tСМО=Робсл![]() =
=![]() =0,1 мин.
=0,1 мин.
В результате объединения каналов в один пропускная способность системы снизилась, так как увеличилась вероятность отказа. Среднее время пребывания заявки в системе уменьшилось.
Пример 2. На вход трехканальной СМО с неограниченной очередью поступает поток заявок с интенсивностью ![]() =4 заявки в час, среднее время обслуживания одной заявки t=1/μ=0,5 ч. Найти показатели эффективности работы системы.
=4 заявки в час, среднее время обслуживания одной заявки t=1/μ=0,5 ч. Найти показатели эффективности работы системы.
Для рассматриваемой системы n=3, ![]() =4, μ=1/0,5=2, ρ=
=4, μ=1/0,5=2, ρ=![]() /μ=2, ρ/n=2/3<1. Определяем вероятность простоя по формуле:
/μ=2, ρ/n=2/3<1. Определяем вероятность простоя по формуле:
Р![]() =
=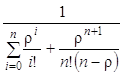 .
.
P0= 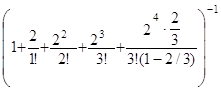 =1/9.
=1/9.
Среднее число заявок в очереди находим по формуле:
L=![]() .
.
L=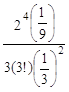 =
=![]() .
.
Среднее время ожидания заявки в очереди считаем по формуле:
t=![]() .
.
t=![]() =
=![]()
![]() 0,22 ч.
0,22 ч.
Среднее время пребывания заявки в системе:
Т=t+![]()
![]() 0,22+0,5=0,72.
0,22+0,5=0,72.
Пример 3. В парикмахерской работают 3 мастера, а в зале ожидания расположены 3 стула. Поток клиентов имеет интенсивность ![]() =12 клиентов в час. Среднее время обслуживания tобсл=20 мин. Определить относительную и абсолютную пропускную способность системы, среднее число занятых кресел, среднюю длину очереди, среднее время, которое клиент проводит в парикмахерской.
=12 клиентов в час. Среднее время обслуживания tобсл=20 мин. Определить относительную и абсолютную пропускную способность системы, среднее число занятых кресел, среднюю длину очереди, среднее время, которое клиент проводит в парикмахерской.
Для данной задачи n=3, m=3, ![]() =12, μ=3, ρ=4, ρ/n=4/3. Вероятность простоя определяем по формуле:
=12, μ=3, ρ=4, ρ/n=4/3. Вероятность простоя определяем по формуле:
Р0=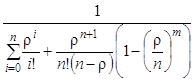 .
.
P0=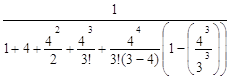
![]() 0,012.
0,012.
Вероятность отказа в обслуживании определяем по формуле
Ротк=Рn+m= ![]() .
.
Pотк=Pn+m![]()

![]() 0,307.
0,307.
Относительная пропускная способность системы, т.е. вероятность обслуживания:
Pобсл=1-Pотк![]() 1-0,307=0,693.
1-0,307=0,693.
Абсолютная пропускная способность:
А=![]() Робсл
Робсл![]() 12
12![]() .
.
Среднее число занятых каналов:
![]() .
.
Средняя длина очереди определяется по формуле:
L=
L=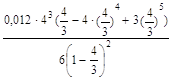
![]() 1,56.
1,56.
Среднее время ожидания обслуживания в очереди:
t=![]() ч.
ч.
Среднее число заявок в СМО:
M=L+![]() .
.
Среднее время пребывания заявки в СМО:
Т=М/![]()
![]() 0,36 ч.
0,36 ч.
Пример 4. Рабочий обслуживает 4 станка. Каждый станок отказывает с интенсивностью ![]() =0,5 отказа в час, среднее время ремонта tрем=1/μ=0,8 ч. Определить пропускную способность системы.
=0,5 отказа в час, среднее время ремонта tрем=1/μ=0,8 ч. Определить пропускную способность системы.
Эта задача рассматривает замкнутую СМО, μ=1,25, ρ=0,5/1,25=0,4. Вероятность простоя рабочего определяем по формуле:
Р0= .
.
P0=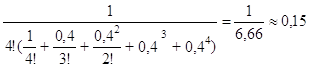 .
.
Вероятность занятости рабочего Рзан=1-Р0![]() . Если рабочий занят, он налаживает μ-станков в единицу времени, пропускная способность системы: А=(1-P0)μ=0,85μ
. Если рабочий занят, он налаживает μ-станков в единицу времени, пропускная способность системы: А=(1-P0)μ=0,85μ ![]() станков в час.
станков в час.
Решение задачи
Задача:
Два рабочих обслуживают группу из четырех станков. Остановки работающего станка происходят в среднем через 30 мин. Среднее время наладки составляет 15 мин. Время работы и время наладки распределено по экспоненциальному закону.
Найдите среднюю долю свободного времени для каждого рабочего и среднее время работы станка.
Найдите те же характеристики для системы, в которой:
а) за каждым рабочим закреплены два станка;
б) два рабочих всегда обслуживают станок вместе, причем с двойной интенсивностью;
в) единственный неисправный станок обслуживают оба рабочих сразу (с двойной интенсивностью), а при появлении еще хотя бы одного неисправного станка они начинают работать порознь, причем каждый обслуживает один станок (вначале опишите систему в терминах процессов гибели и рождения).
Решение:
Возможны следующие состояния системы S:
S0 – все станки исправны;
S1 – 1 станок ремонтируется, остальные исправны;
S2 – 2 станок ремонтируется, остальные исправны;
S3 – 3 станок ремонтируется, остальные исправны;
S4 – 4 станок ремонтируется, остальные исправны;
S5 – (1, 2) станки ремонтируются, остальные исправны;
S6 – (1, 3) станки ремонтируются, остальные исправны;
S7 – (1, 4) станки ремонтируются, остальные исправны;
S8 – (2, 3) станки ремонтируются, остальные исправны;
S9 – (2, 4) станки ремонтируются, остальные исправны;
S10 – (3, 4) станки ремонтируются, остальные исправны;
S11 – (1, 2, 3) станки ремонтируются, 4 станок исправен;
S12 – (1, 2, 4) станки ремонтируются, 3 станок исправен;
S13 – (1, 3, 4) станки ремонтируются, 2 станок исправен;
S14 – (2, 3, 4) станки ремонтируются, 1 станок исправен;
S15 – все станки ремонтируются.
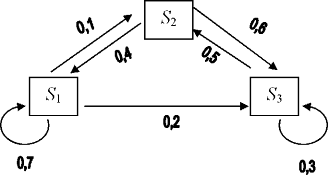
Граф состояний системы…

Данная система S является примером замкнутой системы, так как каждый станок является потенциальным требованием, превращаясь в реальное в момент своей поломки. Пока станок работает, он находится в блоке задержки, а с момента поломки до момента окончания ремонта – в самой системе. Каждый рабочий является каналом обслуживания.
![]()
![]()
![]()
![]()
![]()
![]()
Вероятность простоя рабочего определяется по формуле:

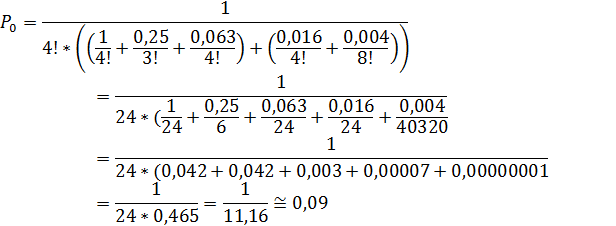
![]() .
.
Вероятность занятости рабочего:
![]() .
.
Если рабочий занят, он налаживает μ-станков в единицу времени, пропускная способность системы:
![]() .
.
Ответ:
Средняя доля свободного времени для каждого рабочего ≈ 0,09.
Среднее время работы станка ≈ 3,64.
а) За каждым рабочим закреплены два станка.
![]()
![]()
![]()
![]()
![]()
![]()
Вероятность простоя рабочего определяется по формуле:

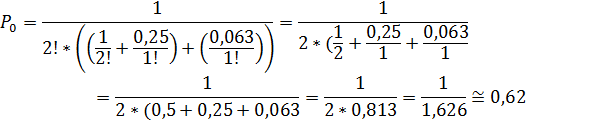
![]() .
.
Вероятность занятости рабочего:
![]() .
.
Если рабочий занят, он налаживает μ-станков в единицу времени, пропускная способность системы:
![]() .
.
Ответ:
Средняя доля свободного времени для каждого рабочего ≈ 0,62.
Среднее время работы станка ≈ 1,52.
б) Два рабочих всегда обслуживают станок вместе, причем с двойной интенсивностью.
в) Единственный неисправный станок обслуживают оба рабочих сразу (с двойной интенсивностью), а при появлении еще хотя бы одного неисправного станка они начинают работать порознь, причем каждый обслуживает один станок (вначале опишите систему в терминах процессов гибели и рождения).
Сравнение 5 ответов:
Наиболее эффективным способом организации рабочих за станками будет являться начальный вариант задачи.
Заключение
Выше были рассмотрены примеры простейших систем массового обслуживания (СМО). Понятие «простейшие» не означает «элементарные». Математические модели этих систем применимы и успешно используются в практических расчетах.
Возможность применения теории принятия решений в системах массового обслуживания определяется следующими факторами:
1. Количество заявок в системе (которая рассматривается как СМО) должно быть достаточно велико (массово).
2. Все заявки, поступающие на вход СМО, должны быть однотипными.
3. Для расчетов по формулам необходимо знать законы, определяющие поступление заявок и интенсивность их обработки. Более того, потоки заявок должны быть Пуассоновскими.
4. Структура СМО, т.е. набор поступающих требований и последовательность обработки заявки, должна быть жестко зафиксирована.
5. Необходимо исключить из системы субъектов или описывать их как требования с постоянной интенсивностью обработки.
К перечисленным выше ограничениям можно добавить еще одно, оказывающее сильное влияние на размерность и сложность математической модели.
6. Количество используемых приоритетов должно быть минимальным. Приоритеты заявок должны быть постоянными, т.е. они не могут меняться в процессе обработки внутри СМО.
В ходе выполнения работы была достигнута основная цель – изучен основной материал «СМО с ограниченным временем ожидания» и «Замкнутые СМО», которая была поставлена преподавателем учебной дисциплины. Также мы ознакомились применением полученных знаний на практике, т.е. закрепили пройденный материал.
Список литературы
1) http://www.5ballov.ru.
2) http://www.studentport.ru.
3) http://vse5ki.ru.
4) http://revolution..
5) Фомин Г.П. Математические методы и модели в коммерческой деятельности. М: Финансы и статистика, 2001.
6) Гмурман В.Е. Теория вероятностей и математическая статистика. М: Высшая школа, 2001.
7) Советов Б.А., Яковлев С.А. Моделирование систем. М: Высшая школа, 1985.
8) Лифшиц А.Л. Статистическое моделирование СМО. М., 1978.
9) Вентцель Е.С. Исследование операций. М: Наука, 1980.
10) Вентцель Е.С., Овчаров Л.А. Теория вероятностей и её инженерные приложения. М: Наука, 1988.
Похожие работы
... и эффективным средством выработки оптимальных управленческий решений, главной особенностью которых в современных условиях становится их своевременность. 2 Применение теории массового обслуживания в экономическом анализе 2.1 Теория массового обслуживания Теория массового обслуживания – вероятностные модели реальных систем обслуживания населения, при которых время обслуживания будет ...
... остальных состояний системы. В результате получим систему уравнений: Решение этой системы будет иметь вид: (4) , ,…, (5) 4. Основные понятия и классификация систем массового обслуживания Заявкой (или требованием) называется спрос на удовлетворение какой-либо потребности (далее потребности предполагаются однотипными). Выполнение ...
... 2-3 Поиск литературы 7 1 7 2-4 Разработка модели разветвленной СМО 6 1 6 3 Поиск литературы завершен 3-6 Изучение литературы по теории массового обслуживания 10 1 10 4 Модель разработана 4-5 Разработка алгоритма программы 10 1 10 5 Алгоритм программы разработан 5-7 Выбор среды программиро-вания и создание программы 30 1 ...
... очередь длины k, остается в ней с вероятностью Pk и не присоединяется к очереди с вероятностью gk=1 - Pk,'. именно так обычно ведут себя люди в очередях. В системах массового обслуживания, являющихся математическими моделями производственных процессов, возможная длина очереди ограничена постоянной величиной (емкость бункера, например). Очевидно, это частный случай общей постановки. Некоторые ...
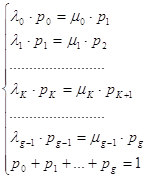
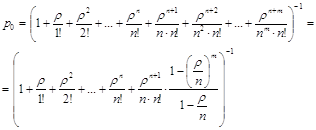
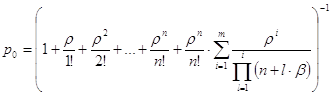

0 комментариев