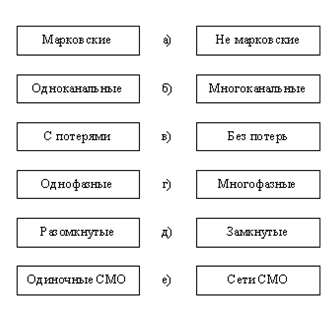
Навигация
Многоканальная СМО с ожиданием
2.2 Многоканальная СМО с ожиданием
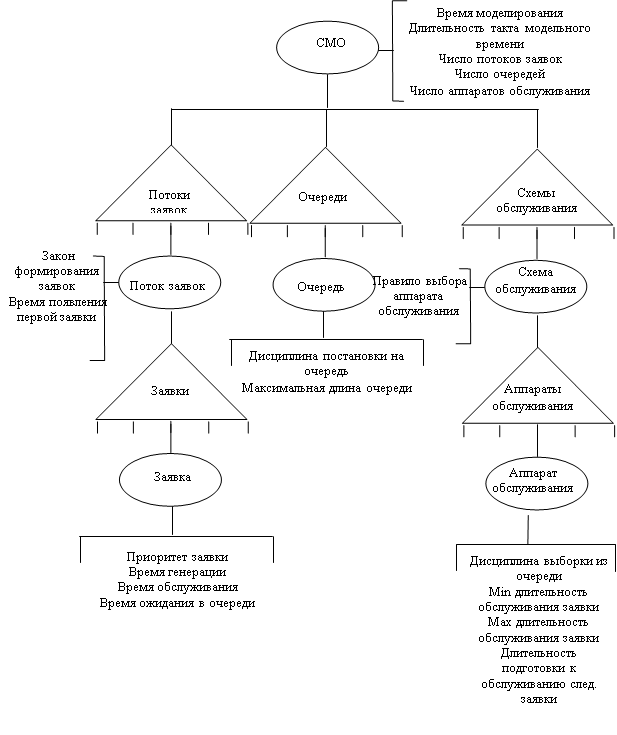
Система с ограниченной длиной очереди. Рассмотрим ![]() канальную СМО с ожиданием, на которую поступает поток заявок с интенсивностью
канальную СМО с ожиданием, на которую поступает поток заявок с интенсивностью ![]() ; интенсивность обслуживания (для одного канала)
; интенсивность обслуживания (для одного канала) ![]() ; число мест в очереди
; число мест в очереди ![]() .
.
Состояния системы нумеруются по числу заявок, связанных системой:
нет очереди:
![]() — все каналы свободны;
— все каналы свободны;
![]() — занят один канал, остальные свободны;
— занят один канал, остальные свободны;
![]() — заняты
— заняты ![]() -каналов, остальные нет;
-каналов, остальные нет;
![]() — заняты все
— заняты все ![]() -каналов, свободных нет;
-каналов, свободных нет;
есть очередь:
![]() — заняты все n-каналов; одна заявка стоит в очереди;
— заняты все n-каналов; одна заявка стоит в очереди;
![]() — заняты все n-каналов, r-заявок в очереди;
— заняты все n-каналов, r-заявок в очереди;
![]() — заняты все n-каналов, r-заявок в очереди.
— заняты все n-каналов, r-заявок в очереди.
ГСП приведен на рис. 17. У каждой стрелки проставлены соответствующие интенсивности потоков событий. По стрелкам слева направо систему переводит всегда один и тот же поток заявок с интенсивностью ![]() , по стрелкам справа налево систему переводит поток обслуживании, интенсивность которого равна
, по стрелкам справа налево систему переводит поток обслуживании, интенсивность которого равна ![]() , умноженному на число занятых каналов.
, умноженному на число занятых каналов.

Рис. 17. Многоканальная СМО с ожиданием
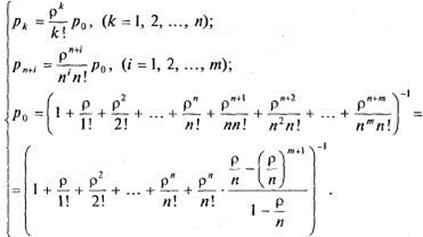
Граф типичен для процессов размножения и гибели, для которой решение ранее получено. Напишем выражения для предельных вероятностей состояний, используя обозначение ![]() : (здесь используется выражение для суммы геометрической прогрессии со знаменателем
: (здесь используется выражение для суммы геометрической прогрессии со знаменателем ![]() ).
).
Таким образом, все вероятности состояний найдены.
Определим характеристики эффективности системы.
Вероятность отказа. Поступившая заявка получает отказ, если заняты все n-каналов и все m-мест в очереди:
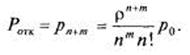 (18)
(18)
Относительная пропускная способность дополняет вероятность отказа до единицы:
![]()
Абсолютная пропускная способность СМО:
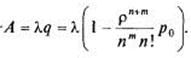 (19)
(19)
Среднее число занятых каналов. Для СМО с отказами оно совпадало со средним числом заявок, находящихся в системе. Для СМО с очередью среднее число занятых каналов не совпадает со средним числом заявок, находящихся в системе: последняя величина отличается от первой на среднее число заявок, находящихся в очереди.
Обозначим среднее число занятых каналов ![]() . Каждый занятый канал обслуживает в среднем
. Каждый занятый канал обслуживает в среднем ![]() -заявок в единицу времени, а СМО в целом обслуживает в среднем А-заявок в единицу времени. Разделив одно на другое, получим:
-заявок в единицу времени, а СМО в целом обслуживает в среднем А-заявок в единицу времени. Разделив одно на другое, получим:
![]() .
.
Среднее число заявок в очереди можно вычислить непосредственно как математическое ожидание дискретной случайной величины:
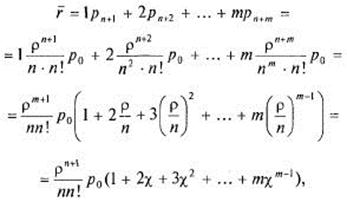 (20)
(20)
где ![]() .
.
Здесь опять (выражение в скобках) встречается производная суммы геометрической прогрессии (см. выше (11), (12) — (14)), используя соотношение для нее, получаем:
![]()
Среднее число заявок в системе:
![]()
Среднее время ожидания заявки в очереди. Рассмотрим ряд ситуаций, различающихся тем, в каком состоянии застанет систему вновь пришедшая заявка и сколько времени ей придется ждать обслуживания.
Если заявка застанет не все каналы занятыми, ей вообще не придется ждать (соответствующие члены в математическом ожидании равны нулю). Если заявка придет в момент, когда заняты все n-каналов, а очереди нет, ей придется ждать в среднем время, равное ![]() (потому что «поток освобождений»
(потому что «поток освобождений» ![]() -каналов имеет интенсивность
-каналов имеет интенсивность ![]() ). Если заявка застанет все каналы занятыми и одну заявку перед собой в очереди, ей придется в среднем ждать в течение времени
). Если заявка застанет все каналы занятыми и одну заявку перед собой в очереди, ей придется в среднем ждать в течение времени ![]() (по
(по ![]() на каждую впереди стоящую заявку) и т. д. Если заявка застанет в очереди
на каждую впереди стоящую заявку) и т. д. Если заявка застанет в очереди ![]() -заявок, ей придется ждать в среднем в течение времени
-заявок, ей придется ждать в среднем в течение времени ![]() . Если вновь пришедшая заявка застанет в очереди уже m-заявок, то она вообще не будет ждать (но и не будет обслужена). Среднее время ожидания найдем, умножая каждое из этих значений на соответствующие вероятности:
. Если вновь пришедшая заявка застанет в очереди уже m-заявок, то она вообще не будет ждать (но и не будет обслужена). Среднее время ожидания найдем, умножая каждое из этих значений на соответствующие вероятности:
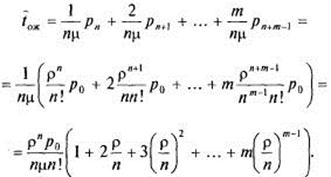 (21)
(21)
Так же, как и в случае одноканальной СМО с ожиданием, отметим, что это выражение отличается от выражения для средней длины очереди (20) только множителем ![]() , т. е.
, т. е.
![]() .
.
Среднее время пребывания заявки в системе, так же, как и для одноканальной СМО, отличается от среднего времени ожидания на среднее время обслуживания, умноженное на относительную пропускную способность:
![]() .
.
Системы с неограниченной длиной очереди. Мы рассмотрели ![]() канальную СМО с ожиданием, когда в очереди одновременно могут находиться не более m-заявок.
канальную СМО с ожиданием, когда в очереди одновременно могут находиться не более m-заявок.
Так же, как и ранее, при анализе систем без ограничений необходимо рассмотреть полученные соотношения при ![]() .
.
Вероятности состояний получим из формул предельным переходом (при ![]() ). Заметим, что сумма соответствующей геометрической прогрессии сходится при
). Заметим, что сумма соответствующей геометрической прогрессии сходится при ![]() и расходится при
и расходится при ![]() >1. Допустив, что
>1. Допустив, что ![]() <1 и устремив в формулах величину m к бесконечности, получим выражения для предельных вероятностей состояний:
<1 и устремив в формулах величину m к бесконечности, получим выражения для предельных вероятностей состояний:
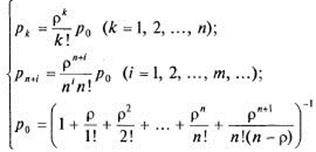 (22)
(22)
Вероятность отказа, относительная и абсолютная пропускная способность. Так как каждая заявка рано или поздно будет обслужена, то характеристики пропускной способности СМО составят:
![]()
Среднее число заявок в очереди получим при ![]() из (20):
из (20):
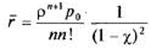 ,
,
а среднее время ожидания — из (21):
![]() .
.
Среднее число занятых каналов ![]() , как и ранее, определяется через абсолютную пропускную способность:
, как и ранее, определяется через абсолютную пропускную способность:
![]() .
.
Среднее число заявок, связанных с СМО, определяется как среднее число заявок в очереди плюс среднее число заявок, находящихся под обслуживанием (среднее число занятых каналов):
![]() .
.
Пример 2. Автозаправочная станция с двумя колонками (n = 2) обслуживает поток машин с интенсивностью ![]() =0,8 (машин в минуту). Среднее время обслуживания одной машины:
=0,8 (машин в минуту). Среднее время обслуживания одной машины:
![]()
В данном районе нет другой АЗС, так что очередь машин перед АЗС может расти практически неограниченно. Найти характеристики СМО.
Имеем:
![]()
Поскольку![]() <1, очередь не растет безгранично и имеет смысл говорить о предельном стационарном режиме работы СМО. По формулам (22) находим вероятности состояний:
<1, очередь не растет безгранично и имеет смысл говорить о предельном стационарном режиме работы СМО. По формулам (22) находим вероятности состояний:
![]()
![]() и т. д.
и т. д.
Среднее число занятых каналов найдем, разделив абсолютную пропускную способность СМО А=![]() =0,8 на интенсивность обслуживания
=0,8 на интенсивность обслуживания ![]() =0,5:
=0,5:
![]()
Вероятность отсутствия очереди у АЗС будет:
![]()
Среднее число машин в очереди:
![]()
Среднее число машин на АЗС:
![]()
Среднее время ожидания в очереди:
![]()
Среднее время пребывания машины на АЗС:
![]()
СМО с ограниченным временем ожидания. Ранее рассматривались системы с ожиданием, ограниченным только длиной очереди (числом m-заявок, одновременно находящихся в очереди). В такой СМО заявка, разраставшая в очередь, не покидает ее, пока не дождется обслуживания. На практике встречаются СМО другого типа, в которых заявка, подождав некоторое время, может уйти из очереди (так называемые «нетерпеливые» заявки).
Рассмотрим СМО подобного типа, предполагая, что ограничение времени ожидания является случайной величиной.
Предположим, что имеется n-канальная СМО с ожиданием, в которой число мест в очереди не ограничено, но время пребывания заявки в очереди является некоторой случайной величиной со средним значением![]() , таким образом, на каждую заявку, стоящую в очереди, действует своего рода пуассоновский «поток уходов» с интенсивностью:
, таким образом, на каждую заявку, стоящую в очереди, действует своего рода пуассоновский «поток уходов» с интенсивностью:
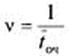
Если этот поток пуассоновский, то процесс, протекающий в СМО, будет марковским. Найдем для него вероятности состояний. Нумерация состояний системы связывается с числом заявок в системе — как обслуживаемых, так и стоящих в очереди:
нет очереди:
![]() — все каналы свободны;
— все каналы свободны;
![]() — занят один канал;
— занят один канал;
![]() — заняты два канала;
— заняты два канала;
![]() — заняты все n-каналов;
— заняты все n-каналов;
есть очередь:
![]() — заняты все n-каналов, одна заявка стоит в очереди;
— заняты все n-каналов, одна заявка стоит в очереди;
![]() — заняты все n-каналов, r-заявок стоят в очереди и т. д.
— заняты все n-каналов, r-заявок стоят в очереди и т. д.
Граф состояний и переходов системы показан на рис. 23.

Рис. 23. СМО с ограниченным временем ожидания
Разметим этот граф, как и раньше; у всех стрелок, ведущих слева направо, будет стоять интенсивность потока заявок ![]() . Для состояний без очереди у стрелок, ведущих из них справа налево, будет, как и раньше, стоять суммарная интенсивность потока обслуживании всех занятых каналов. Что касается состояний с очередью, то у стрелок, ведущих из них справа налево, будет стоять суммарная интенсивность потока обслуживания всех n-каналов
. Для состояний без очереди у стрелок, ведущих из них справа налево, будет, как и раньше, стоять суммарная интенсивность потока обслуживании всех занятых каналов. Что касается состояний с очередью, то у стрелок, ведущих из них справа налево, будет стоять суммарная интенсивность потока обслуживания всех n-каналов ![]() плюс соответствующая интенсивность потока уходов из очереди. Если в очереди стоят r-заявок, то суммарная интенсивность потока уходов будет равна
плюс соответствующая интенсивность потока уходов из очереди. Если в очереди стоят r-заявок, то суммарная интенсивность потока уходов будет равна ![]() .
.
Как видно из графа, имеет место схема размножения и гибели; применяя общие выражения для предельных вероятностей состояний в этой схеме (используя сокращенные обозначения ![]() , запишем:
, запишем:
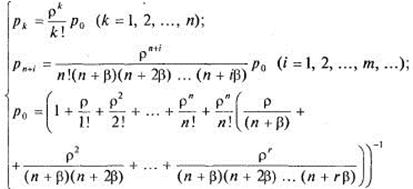 (24)
(24)
Отметим некоторые особенности СМО с ограниченным ожиданием сравнительно с ранее рассмотренными СМО с «терпеливыми» заявками.
Если длина очереди не ограничена и заявки «терпеливы» (не уходят из очереди), то стационарный предельный режим существует только в случае ![]() (при
(при ![]() соответствующая бесконечная геометрическая прогрессия расходится, что физически соответствует неограниченному росту очереди при
соответствующая бесконечная геометрическая прогрессия расходится, что физически соответствует неограниченному росту очереди при ![]() ).
).
Напротив, в СМО с «нетерпеливыми» заявками, уходящими рано или поздно из очереди, установившийся режим обслуживания при ![]() достигается всегда, независимо от приведенной интенсивности потока заявок
достигается всегда, независимо от приведенной интенсивности потока заявок ![]() . Это следует из того, что ряд для
. Это следует из того, что ряд для ![]() в знаменателе формулы (24) сходится при любых положительных значениях
в знаменателе формулы (24) сходится при любых положительных значениях ![]() и
и ![]() .
.
Для СМО с «нетерпеливыми» заявками понятие «вероятность отказа» не имеет смысла — каждая заявка становится в очередь, но может и не дождаться обслуживания, уйдя раньше времени.
Относительная пропускная способность, среднее число заявок в очереди. Относительную пропускную способность q такой СМО можно подсчитать следующим образом. Очевидно, обслужены будут все заявки, кроме тех, которые уйдут из очереди досрочно. Подсчитаем, какое в среднем число заявок покидает очередь досрочно. Для этого вычислим среднее число заявок в очереди:
![]() (25)
(25)
На каждую из этих заявок действует «поток уходов» с интенсивностью ![]() . Значит, из среднего числа
. Значит, из среднего числа ![]() -заявок в очереди в среднем будет уходить, не дождавшись обслуживания,
-заявок в очереди в среднем будет уходить, не дождавшись обслуживания, ![]() -заявок в единицу времени и всего в единицу времени в среднем будет обслуживаться
-заявок в единицу времени и всего в единицу времени в среднем будет обслуживаться ![]() -заявок. Относительная пропускная способность СМО будет составлять:
-заявок. Относительная пропускная способность СМО будет составлять:
![]()
Среднее число занятых каналов ![]() по-прежнему получаем, деля абсолютную пропускную способность А на
по-прежнему получаем, деля абсолютную пропускную способность А на ![]() :
:
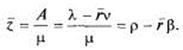 (26)
(26)
Среднее число заявок в очереди. Соотношение (26) позволяет вычислить среднее число заявок в очереди ![]() , не суммируя бесконечного ряда (25). Из (26) получаем:
, не суммируя бесконечного ряда (25). Из (26) получаем:
![]() ,
,
а входящее в эту формулу среднее число занятых каналов можно найти как математическое ожидание случайной величины Z, принимающей значения 0, 1, 2,..., n с вероятностями ![]() ,
,![]() :
:
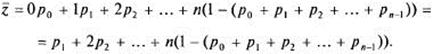 .
.
В заключение заметим, что если в формулах (24) перейти к пределу при ![]() (или, что то же, при
(или, что то же, при ![]() ), то при
), то при ![]() получатся формулы (22), т. е. «нетерпеливые» заявки станут «терпеливыми».
получатся формулы (22), т. е. «нетерпеливые» заявки станут «терпеливыми».
Похожие работы
... и эффективным средством выработки оптимальных управленческий решений, главной особенностью которых в современных условиях становится их своевременность. 2 Применение теории массового обслуживания в экономическом анализе 2.1 Теория массового обслуживания Теория массового обслуживания – вероятностные модели реальных систем обслуживания населения, при которых время обслуживания будет ...
... остальных состояний системы. В результате получим систему уравнений: Решение этой системы будет иметь вид: (4) , ,…, (5) 4. Основные понятия и классификация систем массового обслуживания Заявкой (или требованием) называется спрос на удовлетворение какой-либо потребности (далее потребности предполагаются однотипными). Выполнение ...
... 2-3 Поиск литературы 7 1 7 2-4 Разработка модели разветвленной СМО 6 1 6 3 Поиск литературы завершен 3-6 Изучение литературы по теории массового обслуживания 10 1 10 4 Модель разработана 4-5 Разработка алгоритма программы 10 1 10 5 Алгоритм программы разработан 5-7 Выбор среды программиро-вания и создание программы 30 1 ...
... очередь длины k, остается в ней с вероятностью Pk и не присоединяется к очереди с вероятностью gk=1 - Pk,'. именно так обычно ведут себя люди в очередях. В системах массового обслуживания, являющихся математическими моделями производственных процессов, возможная длина очереди ограничена постоянной величиной (емкость бункера, например). Очевидно, это частный случай общей постановки. Некоторые ...
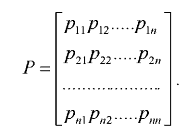

0 комментариев