Релеевское распределение вероятностей случайной величины определяется плотностью вида

35.5. Релеевское распределение вероятностей случайной величины определяется плотностью вида

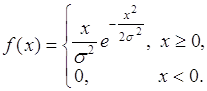(35.10)

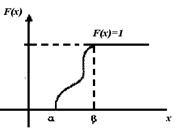
Этой плотности соответствует функция распределения вероятностей  при  и равная

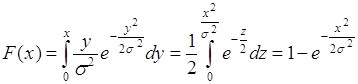(35.11)

при .

35.6. Рассмотрим примеры построения функции распределения и плотности дискретной случайной величины. Пусть случайная величина  - это число успехов в последовательности из  независимых испытаний. Тогда случайная величина  принимает значения ,  с вероятностью , которая определяется формулой Бернулли:

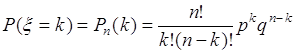 , (35.12)

где ,  - вероятности успеха и неуспеха в одном опыте. Таким образом, функция распределения вероятностей случайной величины  имеет вид

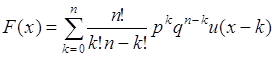, (35.13)

где  - функция единичного скачка. Отсюда плотность распределения:

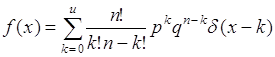, (35.14)

где  - дельта-функция.

Сингулярные случайные величины

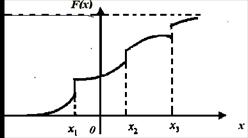
Кроме дискретных и непрерывных случайных величин существуют еще так называемые сингулярные случайные величины. Эти случайные величины характеризуются тем, что их функция распределения вероятностей  - непрерывна, но точки роста  образуют множество нулевой меры. Точкой роста  функции  называется значение ее аргумента  такое, что производная .

Таким образом,  почти всюду на области определения функции. Функцию, удовлетворяющую этому условию, также называют сингулярной. Примером сингулярной функции распределения является кривая Кантора (рис. 36.1), которая строится следующим образом. Полагается при  и  при . Затем интервал  разбивается на три равных части (сегмента) и для внутреннего сегмента  определяется значение  - как полусумма уже определенных значений на ближайших сегментах справа и слева. На данный момент функция  определена для , ее значение , и для  со значением . Полусумма этих значений равна  и определяет значение  на внутреннем сегменте . Затем рассматриваются отрезки

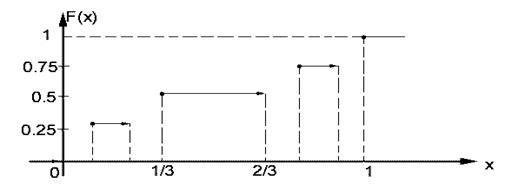
Рис. 36.1. Построение кривой Кантора.

 и , каждый из них разбивается на три равных сегмента и функция  определяется на внутренних сегментах как полусумма ближайших справа и слева заданных значений функции . Таким образом, при  функция  - как полусумма чисел  и . Аналогично на интервале  функция . Затем функция  определяется на интервале , на котором  и т.д.

Суммарная длина всех внутренних сегментов равна

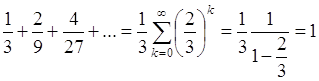
Поэтому, рассматривая интервал , говорят что функция  - постоянная на множестве меры 1, на множестве меры 0 растет, но без скачков.

Известна теорема Лебега. Любая функция распределения  может быть единственным образом представлена в виде суммы трех компонент: дискретной, непрерывной и сингулярной.

Сингулярные распределения практически не встречаются в реальных задачах и поэтому исключаются из нашего дальнейшего изучения.

Математическое ожидание случайной величины

37.1. Функция распределения вероятностей или плотность вероятности являются полными вероятностными характеристиками случайной величины. Однако, во многих задачах такая полная характеристика случайной величины, с одной стороны, может быть неизвестна для исследователя, а с другой стороны и не обязательна, достаточно ограничиться значением некоторых параметров распределения вероятностей, т.е. некоторых чисел (или числовых характеристик). Здесь уместна аналогия с геометрическим описанием сложной формы твердого тела, когда ограничиваются такими характеристиками (числами) как длина, ширина, высота, объем, момент инерции, и т.д., а детальное описание сложной формы этого тела не рассматривается. Числовыми характеристиками случайных величин чаще всего служат так называемые моменты распределения, простейшим из которых является математическое ожидание случайной величины.

Прежде чем вводить определение математического ожидания случайной величины, рассмотрим выражение среднего арифметического результатов измерения дискретной случайной величины. Пусть случайная величина  может принимать значения  соответственно с вероятностями . Результат измерения случайной величины  в каждом опыте - это одно из чисел . Пусть выполнено  опытов, среди них в  опытах случайная величина  принимала значение , в  опытах - значение ,..., в  опытах - значение . Очевидно,  - полное число опытов. Пусть  - среднее арифметическое результатов измерения случайной величины  в  опытах, тогда

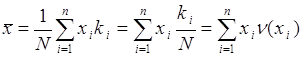, (37.1)

где  - частота появления числа  при измерении случайной величины  в  опытах. С увеличением числа опытов  величина  приближается к числу . Поэтому для того, чтобы определить теоретический аналог среднего арифметического  достаточно в формуле (37.1) частоту  заменить на вероятность . Это приводит к следующему определению.

Математическим ожиданием (средним, статистическим средним) дискретной случайной величины , принимающей значения  с вероятностями , называется число

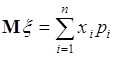. (37.2)

Если множество значений дискретной случайной величины счетно: , то в (37.2) полагается .

Пусть  - однозначная функция одной переменной,  - дискретная случайная величина, принимающая значения  с вероятностями . Тогда  - дискретная случайная величина, принимающая значения  с вероятностями . Поэтому из определения (37.2) математического ожидания следует

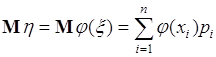(37.3)

- выражение, определяющее математическое ожидание функции .

Математическим ожиданием непрерывной случайной величины  с плотностью распределения вероятностей  называется число

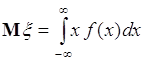 . (37.4)

Аналогично определяется математическое ожидание случайной величины  - как число

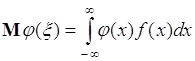, (37.5)

где  - однозначная функция одной переменной,  - плотность распределения вероятностей случайной величины .

37.2. Определения (37.2) и (37.4) согласуются друг с другом. Соотношение (37.4) можно представить приближенно в виде интегральной суммы:

 , (37.6)

где  - малая величина. Тогда , и следовательно, (37.4) формально представимо суммой (37.2).

Если  - дискретная величина, принимающая значения  с вероятностями , то ее плотность вероятности  можно представить через - функцию:

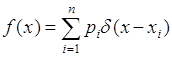. (37.7)

Подставим (37.7) в (37.4), тогда

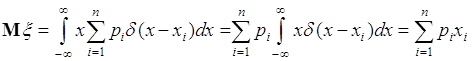 , (37.8)

что совпадает с (37.2). Таким образом, определение (37.4) математического ожидания можно использовать как универсальное определение как для непрерывных, так и для дискретных случайных величин. Однако вычислять математическое ожидание дискретной случайной величины, конечно, удобнее по формуле (37.2).

Выражение (37.4) можно представить через функцию распределения  случайной величины . Для этого выполним следующие преобразования: 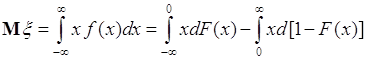. Далее используем для вычисления интеграла способ «по частям»:

.

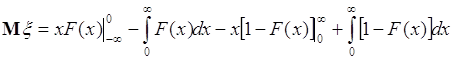Пусть функция  удовлетворяет условиям: , , тогда

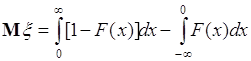 . (37.9)

Это выражение позволяет вычислять математическое ожидание  через функцию распределения.

Примеры вычисления математического ожидания случайной величины

38.1. Пусть гауссова случайная величина  имеет плотность распределения вероятностей (35.4). Вычислим ее математическое ожидание. Для этого подставим выражение (35.4) в формулу (37.4), тогда

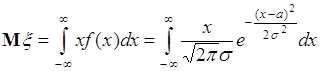. (38.1)

Вместо переменной интегрирования  введем новую переменную , , тогда

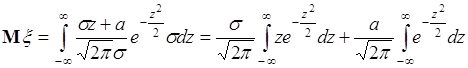. (38.2)

Функция  является нечетной, поэтому интеграл в первом сла­гаемом (38.2) равен нулю. Во втором слагаемом

. (38.3)

Это равенство представляет собой условие нормировки для гауссовой плотности распределения вероятностей (35.4) с параметрами:  и . Таким об­разом, из (38.2) следует  - среднее гауссовой случайной величины является параметром плотности распределения вероятностей (35.4). В дан­ном случае  имеет геометрическую интерпретацию (рис. 35.2) как значе­ние аргумента , при котором плотность (35.4) принимает максимальное значение. В дальнейшем символ  используется также и для обозна­чения среднего любой случайной величины .

38.2. Вычислим среднее случайной величины , распределенной по экспоненциальному закону (35.8):

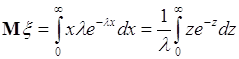. (38.4)

Далее используем способ интегрирования «по частям»:

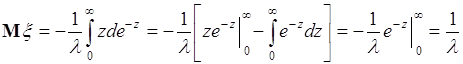. (38.5)

38.3. Пусть  - число успехов в серии из  независимых опытов. Тогда вероятности ,  определяются формулой Бер­нули. Поэтому

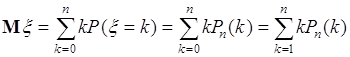. (38.6)

Последнее равенство справедливо, поскольку . Подставим в (38.6) формулу Бернули, тогда:

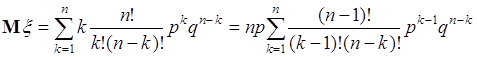. (38.7)

Введем новый индекс суммирования , тогда

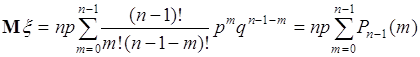. (38.8)

Поскольку  - вероятность  успехов в серии из  опытов, то 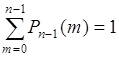 - как вероятность достоверного события, состоящего в появ­лении любого числа успехов в интервале . Поэтому из (38.8) следует

. (38.9)

38.4. Однако не у всякой случайной величины существует ее математи­ческое ожидание. Причиной этого является расходимость интеграла (37.4), что в свою очередь, обусловлено малой скоростью сходимости к нулю плот­ности  при , так что для функции  не существует интеграл вида (37.4). Для примера рассмотрим вычисление математического ожида­ния случайной величины , распределенной по закону Коши: .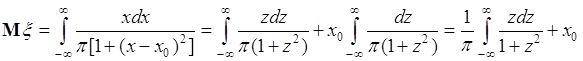

(38.10)

Здесь несобственный интеграл расходится, так как

.

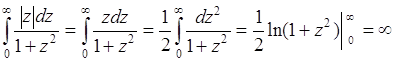Следовательно, случайная величина  не имеет математического ожидания. Однако, если интеграл в (38.10) понимать в смысле главного значения Коши, то

,

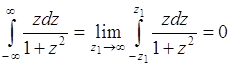 поскольку функция  является не­четной. Следовательно, при этом

. (38.11)

 

Свойства математического ожидания

Основные свойства математического ожидания следуют непосредственно из свойств интеграла в определении (37.5):

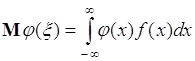. (39.1)

1. Пусть  представляет собой постоянную , тогда из (39.1) следует

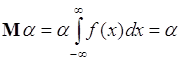, (39.2)

поскольку для плотности  выполняется условие нормировки (33.6). Таким образом, математическое ожидание постоянной равно самой постоянной.

2. Пусть , где  - число и  - однозначная функция одной переменной, тогда из (39.1) следует

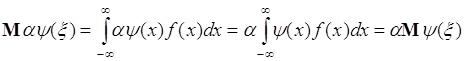. (39.3)

Таким образом, постоянный множитель  можно вынести за знак математического ожидания.

3. Пусть , где  - числа,  - однозначные функции одной переменной, тогда из (39.1) следует

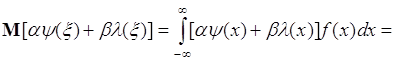
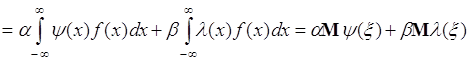. (39.4)

Из этого равенства при  следует свойство 2, а при  и  - свойство 1.

Математическое ожидание  - это число, которое ставится в соответствие случайной величине . Поэтому  можно рассматривать как операцию (оператор, функцию) над случайной величиной . В соответствии со свойствами 1-3 оператор математического ожидания является линейным оператором.

Дисперсия случайной величины

40.1. Дисперсией случайной величины  называется число

. (40.1)

Дисперсия является удобной характеристикой разброса значений  около ее среднего значения . Часто используется для обозначения дисперсии символ . Тогда  называется среднеквадратическим уклонением случайной величины . Если дисперсия имеет размерность квадрата случайной величины, то размерность  совпадает с размерностью случайной величины. Из (40.1) в соответствии со свойствами математического ожидания следует

. (40.2)

Таким образом,

. (40.3)

Если  дискретная случайная величина со значениями  и соответствующими вероятностями , то ее дисперсия

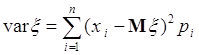(40.4)

Если  - непрерывная случайная величина и  - ее плотность вероятности, то

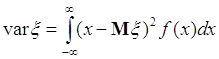. (40.5)

40.2. Рассмотрим примеры. Вычислим дисперсию нормальной случайной величины. Ее плотность  определяется формулой (35.4). Подставим  в (40.5), тогда

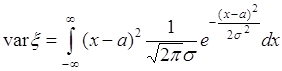. (40.6)

Пусть , тогда ,

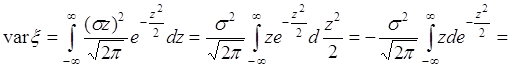
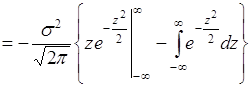 . (40.7)

Подстановка пределов в (40.7) дает нулевые результаты, а интеграл равен . Поэтому

. (40.8)

Таким образом, параметр  в плотности нормальной случайной величины является дисперсией этой величины, а среднеквадратичное уклонение  определяет эффективную ширину плотности : значение  в  раз меньше значения  - в точке максимума.

40.3. В некоторых случаях для вычисления дисперсии удобно использовать формулу (40.3). Например, для экспоненциально распределенной случайной величины  плотность имеет вид (35.8), а ее среднее . Вычислим

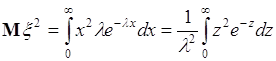. (40.9)

Интеграл в (40.9) вычисляется по частям:

.

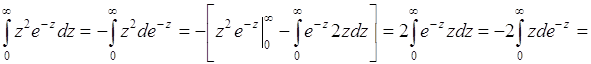
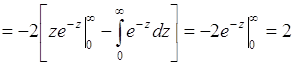Таким образом, . Полученный результат подставим в формулу (40.3), тогда

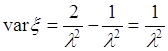. 40.10)

40.4. Вычислим дисперсию числа успехов в вероятностной схеме Бернулли, как пример вычисления дисперсии дискретной случайной величины. При этом также используем формулу (40.3), т.е. на первом шаге вычислим среднее от квадрата , а затем используя ранее полученный результат, дисперсию по формуле (40.3). Итак, среднее от квадрата

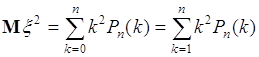, (40.11)

где  - распределение вероятностей Бернулли, поэтому

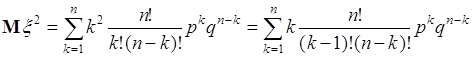. (40.12)

Пусть , тогда  и

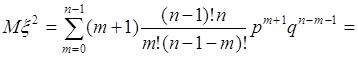
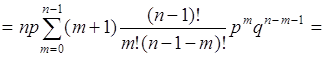
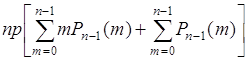.(40.13)

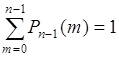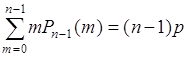Здесь  - вероятность появления  успехов в последовательности из  опытов. Поэтому , как вероятность достоверного события, состоящего в том, что число успехов будет любым в интервале от  до . Первая сумма в (40.13)  как математическое ожидание числа успехов в последовательности из  опытов в соответствии с формулой (38.9). Подставим эти результаты в (40.13), тогда

. (40.14)

Теперь

. (40.15)

Моменты случайной величины