Навигация
О компьютерном моделировании случайных величин
М.В. Кретов
1. Моделирование случайной величины, распределенной по равномерному законуНепрерывная случайная величина ![]() имеет равномерное распределение на отрезке
имеет равномерное распределение на отрезке ![]() , если ее функция распределения задается следующей формулой:
, если ее функция распределения задается следующей формулой:
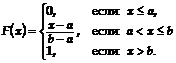 ,
,
Плотность распределения вероятностей при этом имеет вид:
![]()
Математическое ожидание и дисперсия случайной величины ![]() соответственно равны [3]:
соответственно равны [3]:
![]() ,
, ![]() .
.
Обозначим буквой ![]() случайную величину с равномерным распределением на отрезке
случайную величину с равномерным распределением на отрезке ![]() . Для этой случайной величины функция распределения и плотность распределения вероятностей соответственно имеют вид:
. Для этой случайной величины функция распределения и плотность распределения вероятностей соответственно имеют вид:
![]()
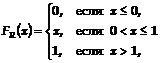 ,
,
![]()
Если ![]()
![]() , то вероятность
, то вероятность
![]()
Моделировать случайную величину ![]() можно многими способами [1].
можно многими способами [1].
Мы рассмотрим метод псевдослучайных последовательностей, который наиболее просто реализуется в компьютере. Для получения псевдослучайной последовательности используем алгоритм, который называется методом середины квадратов [4]. Поясним его на примере. Возьмем некоторое число ![]() . Пусть
. Пусть ![]() Возведем его в квадрат:
Возведем его в квадрат: ![]() Выберем четыре средние цифры этого числа и положим
Выберем четыре средние цифры этого числа и положим ![]() Затем возводим
Затем возводим ![]() в квадрат:
в квадрат: ![]() и снова выбираем четыре средние цифры. Получаем
и снова выбираем четыре средние цифры. Получаем ![]() Далее находим
Далее находим ![]()
![]()
![]()
![]() и т. д. Последовательность чисел
и т. д. Последовательность чисел ![]() принимают за последовательность значений случайной величины
принимают за последовательность значений случайной величины ![]() имеющей равномерное распределение на отрезке
имеющей равномерное распределение на отрезке ![]() . Для оценки степени приближения последовательности
. Для оценки степени приближения последовательности ![]() к последовательности случайных чисел с равномерным распределением используют статистические критерии, например, аналогичные критерию, который используется в работе [2].
к последовательности случайных чисел с равномерным распределением используют статистические критерии, например, аналогичные критерию, который используется в работе [2].
Пусть проводится последовательность ![]() независимых испытаний. В результате каждого испытания может произойти одно из
независимых испытаний. В результате каждого испытания может произойти одно из ![]() несовместных событий
несовместных событий ![]() объединение которых совпадает с пространством элементарных событий
объединение которых совпадает с пространством элементарных событий ![]() . Известна вероятность появления каждого события
. Известна вероятность появления каждого события ![]() ,
, ![]() , которая не изменяется при переходе от одного испытания к другому. Очевидно, что
, которая не изменяется при переходе от одного испытания к другому. Очевидно, что ![]() .
.
Моделирование последовательности испытаний проводится следующим образом. Разделим отрезок ![]() на
на ![]() участков
участков ![]() длины которых соответственно равны
длины которых соответственно равны ![]() Получаем последовательность значений
Получаем последовательность значений ![]() случайной величины
случайной величины ![]() Если
Если ![]() , то считаем, что в
, то считаем, что в ![]() -м испытании наступило событие
-м испытании наступило событие ![]() , так как
, так как
![]() .
.
Похожие работы
... 2. Таблица 2. Устранение недостатков анализа чувствительности и анализа сценариев при использовании для риск-анализа метода Монте-Карло Метод Недостаток Решение с помощью имитационного моделирования Анализ чувствительности Не учитывается наличие корреляции между различными составляющими проекта Корреляция моделируется различными методами и учитывается в модели Рассматривается влияние ...
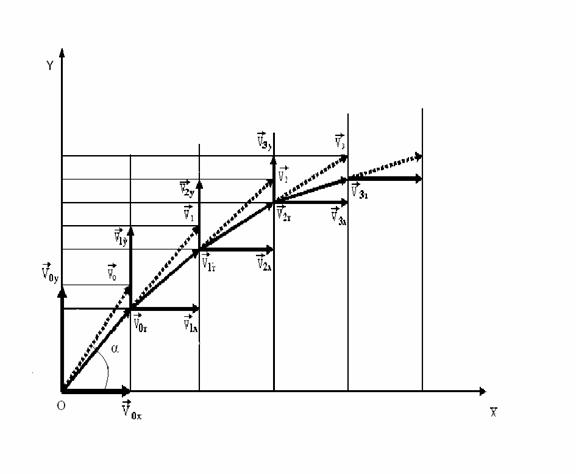
... порыв ветра, интенсивность горения пороха, влажность и т.д. Из всех случайных величин рассмотрим только сопротивление воздуха. Учитывая то, что сопротивление воздуха направленно в противоположную сторону движения тела [4], то силу сопротивления можно представить в виде двух составляющих: вертикальной и горизонтальной, при этом, чем выше скорость, тем больше сопротивление и наоборот. Выделим ...
... как точки на временной оси. Для достижения основной цели моделирования достаточно наблюдать систему в моменты реализации основных событий. Рассмотрим пример одноканальной системы массового обслуживания. Целью имитационного моделирования подобной системы является определение оценок ее основных характеристик, таких, как среднее время пребывания заявки в очереди, средняя длина очереди и доля ...
... тех же условий анализа. Так, в точке эквивалентности при титровании 0,01 М AgNO3 глицином величина рAg оказалaсь: по потенциометрическим данным - 4,2, по результатам компьютерного моделирования - 3,5; соответственно при титровании 0,0010 М AgNO3 комплексоном III - 5,6 и 4,9. Невелики (менее 10%) и расхождения по объему титранта, соответствующему точке эквивалентности. Отмеченные расхождения можно ...


0 комментариев