Навигация
72.2. Функции вида
![]() ,
(72.8)
,
(72.8)
где целые числа ![]() , называются начальными моментами порядка
, называются начальными моментами порядка ![]() случайного процесса
случайного процесса ![]() .
Аналогично центральные моменты определяются соотношениями:
.
Аналогично центральные моменты определяются соотношениями:
![]() .
(72.9)
.
(72.9)
Для функций (72.8), (72.9) используется общее название - моментные функции. Наиболее простые моментные функции (до второго порядка) - это рассмотренные выше математическое ожидание ![]() , дисперсия
, дисперсия ![]() корреляционная и ковариационная функции
корреляционная и ковариационная функции ![]() ,
, ![]() , - находят широкое практическое применение в экспериментальных исследованиях в отличие от моментов более высоких порядков, которые используютя только в теоретических расчетах.
, - находят широкое практическое применение в экспериментальных исследованиях в отличие от моментов более высоких порядков, которые используютя только в теоретических расчетах.
Если задана ![]() - мерная плотность распределения вероятности случайного процесса
- мерная плотность распределения вероятности случайного процесса ![]() , тогда условная плотность
, тогда условная плотность ![]() порядка
порядка ![]() при условии, что случайный процесс в моменты времени
при условии, что случайный процесс в моменты времени ![]() принимает значения
принимает значения ![]() определяется по формуле:
определяется по формуле:
![]()
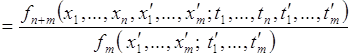 .
(73.1)
.
(73.1)
Соответствующая условная функция распределения вероятностей ![]() порядка
порядка ![]() при условии, что случайный процесс в моменты времени
при условии, что случайный процесс в моменты времени ![]() принимает значения
принимает значения ![]() определяется соотношением:
определяется соотношением:
![]()
![]() .
(73.2)
.
(73.2)
Соотношения между условной плотностью ![]() и условной функцией распределения вероятностей
и условной функцией распределения вероятностей ![]() аналогичны соотношениям для соответствующих безусловных функций, например, справедливо равенство:
аналогичны соотношениям для соответствующих безусловных функций, например, справедливо равенство:
![]()
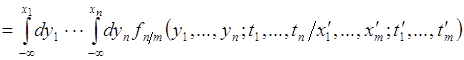 . (72.3)
. (72.3)
В простейшем варианте при ![]() формула (73.1) для условных плотностей принимает вид:
формула (73.1) для условных плотностей принимает вид:
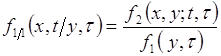 . (73.4)
. (73.4)
Отсюда
![]() . (73.5)
. (73.5)
Поскольку плотность второго порядка симметрична относительно перестановок пар ![]() и
и ![]() , то из (73.5) следует
, то из (73.5) следует
![]() . (73.6)
. (73.6)
Соотношения (73.5), (73.6) - это формулы умножения для плотностей. Очевидна аналогия этих формул с формулой умножения вероятностей. Используя свойство согласованности, из (73.6) получим
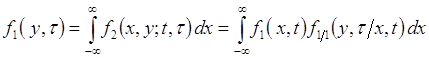 . (73.7)
. (73.7)
Это соотношения аналогично формуле полной вероятности. Далее, выражения (73.6), (73.7) подставим в (73.4), тогда
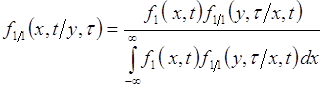 . (73.8)
. (73.8)
Данное соотношение представляет собой аналог формулы Байеса.
Примеры математических моделей случайных процессов
Из соотношения (73.1) следует
![]()
![]() . (74.1)
. (74.1)
Отметим, что здесь произведение первых двух сомножителей, согласно (73.1), равно
![]() . (74.2)
. (74.2)
Аналогично, произведение первых трех сомножителей в (74.1) равно
![]() . (74.3)
. (74.3)
74.1. Случайный процесс ![]() называется процессом с независимыми значениями, если случайные величины
называется процессом с независимыми значениями, если случайные величины ![]() независимы в совокупности для любого
независимы в совокупности для любого ![]() и всех различных
и всех различных ![]() . При этом соотношение (74.1) принимает вид:
. При этом соотношение (74.1) принимает вид:
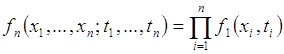 . (74.4)
. (74.4)
Таким образом, ![]() - мерная плотность распределения вероятности
- мерная плотность распределения вероятности ![]() случайного процесса с независимыми значениями полностью определяется через его одномерную плотность вероятности
случайного процесса с независимыми значениями полностью определяется через его одномерную плотность вероятности ![]() . Столь простая структура
. Столь простая структура ![]() - мерной плотности позволяет во многих случаях легко находить решения задач. Однако, столь простая математическая модель (74.4) может оказаться неадэкватной исследуемому процессу. Тогда результаты теоретических расчетов, основанные на формуле (74.4), не соответствуют результатам опыта, и возникает необходимость построения более сложной математической модели исследуемого процесса с учетом статистических связей между его различными сечениями
- мерной плотности позволяет во многих случаях легко находить решения задач. Однако, столь простая математическая модель (74.4) может оказаться неадэкватной исследуемому процессу. Тогда результаты теоретических расчетов, основанные на формуле (74.4), не соответствуют результатам опыта, и возникает необходимость построения более сложной математической модели исследуемого процесса с учетом статистических связей между его различными сечениями ![]() ,
, ![]() , что позволит получить более точное описание свойств исследуемого процесса.
, что позволит получить более точное описание свойств исследуемого процесса.
74.2. Случайный процесс ![]() называется процессом с ортогональными значениями, если
называется процессом с ортогональными значениями, если
![]() (74.5)
(74.5)
для любых моментов времени ![]() .
.
74.3. Случайный процесс ![]() называется процессом с независимыми приращениями, если случайные величины
называется процессом с независимыми приращениями, если случайные величины ![]() и
и ![]() независимы для любых неперекрывающихся отрезков
независимы для любых неперекрывающихся отрезков ![]() ,
, ![]() .
.
74.4. Пусть моменты времени ![]() - упорядочены по индексу. Случайный процесс
- упорядочены по индексу. Случайный процесс ![]() называется марковским, если его условная плотность вероятности удовлетворяет равенству:
называется марковским, если его условная плотность вероятности удовлетворяет равенству:
![]() . (74.6)
. (74.6)
Таким образом, для марковского процесса случайная величина ![]() зависит только от
зависит только от ![]() и не зависит от всех
и не зависит от всех ![]() ,
, ![]() . Принято говорить, что марковский процесс помнит свою историю только на один шаг.
. Принято говорить, что марковский процесс помнит свою историю только на один шаг.
Соотношение (74.1) для марковского процесса принимает вид:
![]() .
.
(74.7)
Отсюда следует, что, ![]() - мерная плотность распределения вероятности
- мерная плотность распределения вероятности ![]() случайного марковского процесса полностью определяется его двумерной плотностью
случайного марковского процесса полностью определяется его двумерной плотностью ![]() , поскольку одномерная плотность
, поскольку одномерная плотность ![]() и условная
и условная ![]() определяются через
определяются через ![]() по формулам (73.7) и (73.4).
по формулам (73.7) и (73.4).
Марковский процесс можно рассматривать как обобщение процесса с независимыми значениями, в том смысле, что последний не помнит свою историю, а марковский процесс помнит свою историю на один шаг. Но и марковский процесс можно усложнить, удлиняя его память на два шага, на три шага и т.д. В результате получаются более точные математические модели исследуемого процесса, что, однако, достигается их усложнением. Такие модели также принято называть марковскими процессами, но самая простая из них, с памятью в один шаг (74.7), в этом ряду называется простейшим марковским процессом.
Стационарные процессы
75.1. Случайный процесс ![]() называется строго стационарным, если его
называется строго стационарным, если его ![]() - мерная плотность вероятности удовлетворяет условию:
- мерная плотность вероятности удовлетворяет условию:
![]() (75.1)
(75.1)
для любого ![]() . Отсюда при
. Отсюда при ![]() и
и ![]() получим
получим
![]() .
(75.2)
.
(75.2)
Это равенство означает, что плотность первого порядка ![]() не зависит от времени
не зависит от времени ![]() . При этом математическое ожидание случайного процесса
. При этом математическое ожидание случайного процесса
 (75.3)
(75.3)
- величина постоянная, не зависимая от времени. Аналогично, постоянными для этого процесса являются среднее квадрата ![]() и дисперсия
и дисперсия ![]() . Пусть
. Пусть ![]() и
и ![]() , тогда из (75.1) следует равенство
, тогда из (75.1) следует равенство
![]() . (75.4)
. (75.4)
Таким образом, плотность второго порядка ![]() зависит от временных аргументов
зависит от временных аргументов ![]() через их разность
через их разность ![]() . Поэтому корреляционная функция
. Поэтому корреляционная функция ![]() и ковариационная функция
и ковариационная функция ![]() также являются функциями разности
также являются функциями разности ![]() своих аргументов.
своих аргументов.
В общем случае в соотношении (75.1) можно положить, например, ![]() , тогда плотность
, тогда плотность ![]() зависит от
зависит от ![]() временных аргументов
временных аргументов ![]() Следовательно, моментные функции, которые в общем случае зависят от
Следовательно, моментные функции, которые в общем случае зависят от ![]() временных аргументов
временных аргументов ![]() , для строго стационарных случайных процессов также зависят от
, для строго стационарных случайных процессов также зависят от ![]() временных аргументов
временных аргументов ![]()
75.1. Раздел теории случайных процессов, в котором излагаются основные свойства функций ![]() и
и ![]() , принято называть корреляционной теорией случайных процессов. Таким образом, в рамках корреляционной теории рассматриваются моментные функции не более, чем второго порядка. В связи с этим вводится специальное определение стационарности.
, принято называть корреляционной теорией случайных процессов. Таким образом, в рамках корреляционной теории рассматриваются моментные функции не более, чем второго порядка. В связи с этим вводится специальное определение стационарности.
Случайный процесс ![]() называется стационарным в широком смысле (по Хинчину), если его математическое ожидание
называется стационарным в широком смысле (по Хинчину), если его математическое ожидание ![]() и дисперсия
и дисперсия ![]() - величины постоянные, не зависимые от времени
- величины постоянные, не зависимые от времени ![]() , а корреляционная функция
, а корреляционная функция ![]() зависит от аргументов
зависит от аргументов ![]() через их разность
через их разность ![]() .
.
1. Вентцель Е.С. Теория вероятностей: Учебник для вузов. М.: Высшая школа, 1999. - 575с.
2. Коваленко И.Н., Филиппова А.А. Теория вероятностей и математическая статистика. М.: Высшая школа, 1973. - 368с.
3. Вентцель Е.С., Овчаров Л.А. Теория вероятностей и ее инженерные приложения М.: Высшая школа, 2000. - 480с.
4. Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 1999. - 479с.
5. Пытьев Ю.П., Шишмарев И.А. Курс теории вероятностей и математической статистики для физиков. М.: Изд-во Моск. ун-та, 1983. - 256с.
6. Пугачев В.С. Теория вероятностей и математическая статистика. М.: Наука, 1979. - 496с.
7. Колемаев В.А., Староверов О.В., Турундаевский В.Б. Теория вероятностей и математическая статистика. М.: Высшая школа, 1991. - 400с.
8. Фигурин В.А., Оболонкин В.В. Теория вероятностей и математическая статистика. М.: Новое знание, 2000. - 206с.
9. Чистяков В.П. Курс теории вероятностей. М.: Наука, 1982. - 256с.
10. Боровков А.А. Теория вероятностей. М.: Наука, 1976. - 352с.
11. Кремер Н.Ш. Теория вероятностей и математическая статистика. М.: ЮНИТИ, 2000. - 543с.
Похожие работы
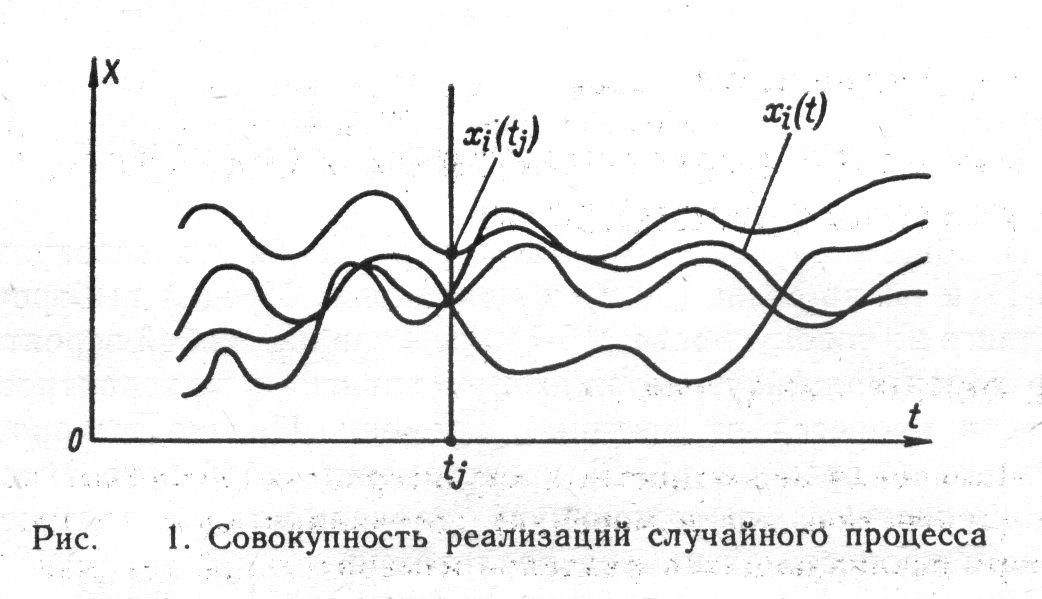
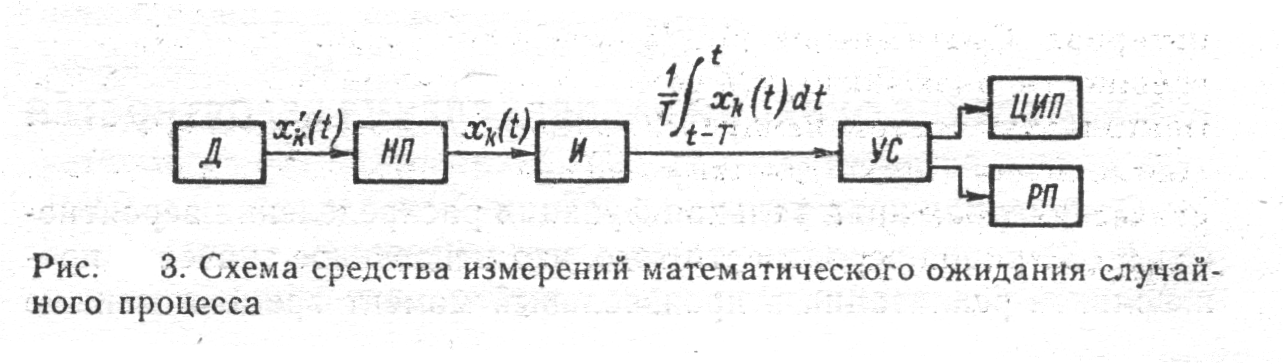
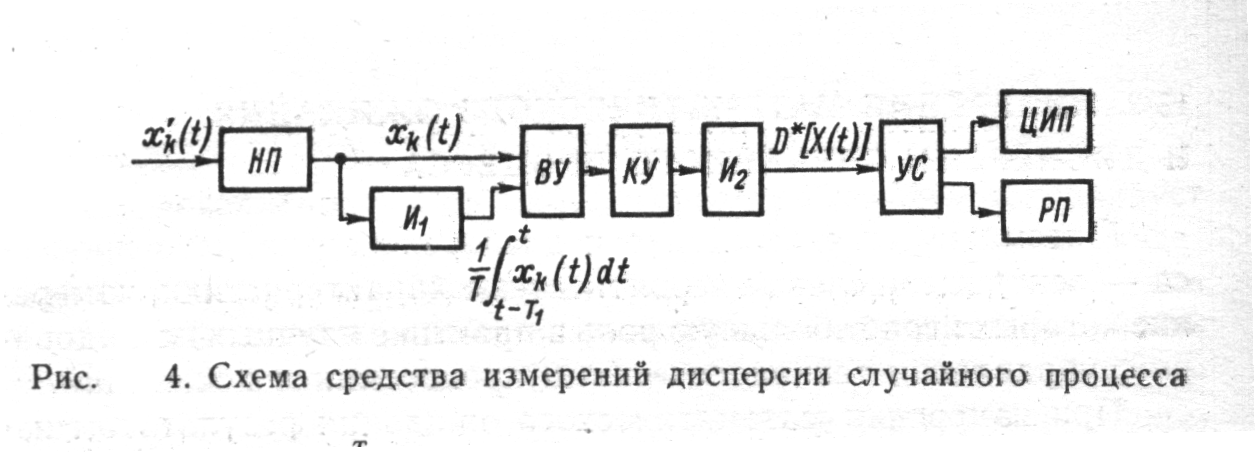
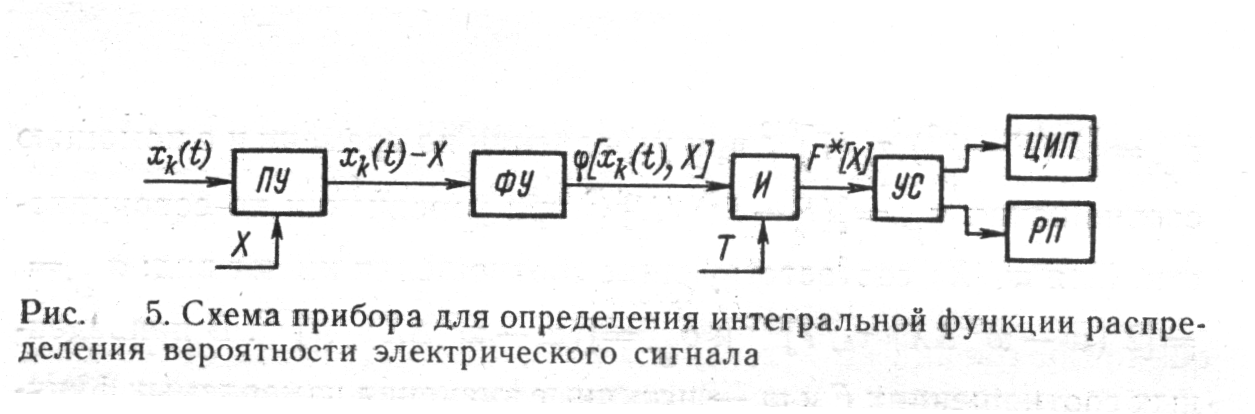
... описание производится с помощью систем вероятностных характеристик: многомерных функций распределения вероятности, моментных функций, характеристических функций и т. п. В теории статистических измерений исследуемый случайный процесс представляется своими реализациями, причем полное представление осуществляется с помощью так называемого ансамбля, т. е. бесконечной совокупностью реализаций. ...
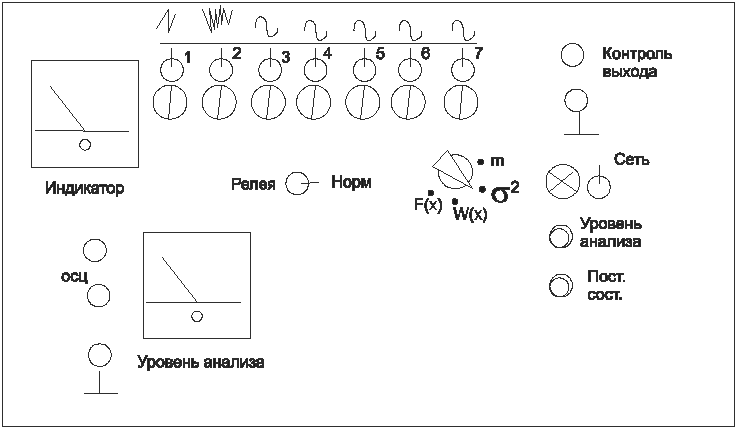
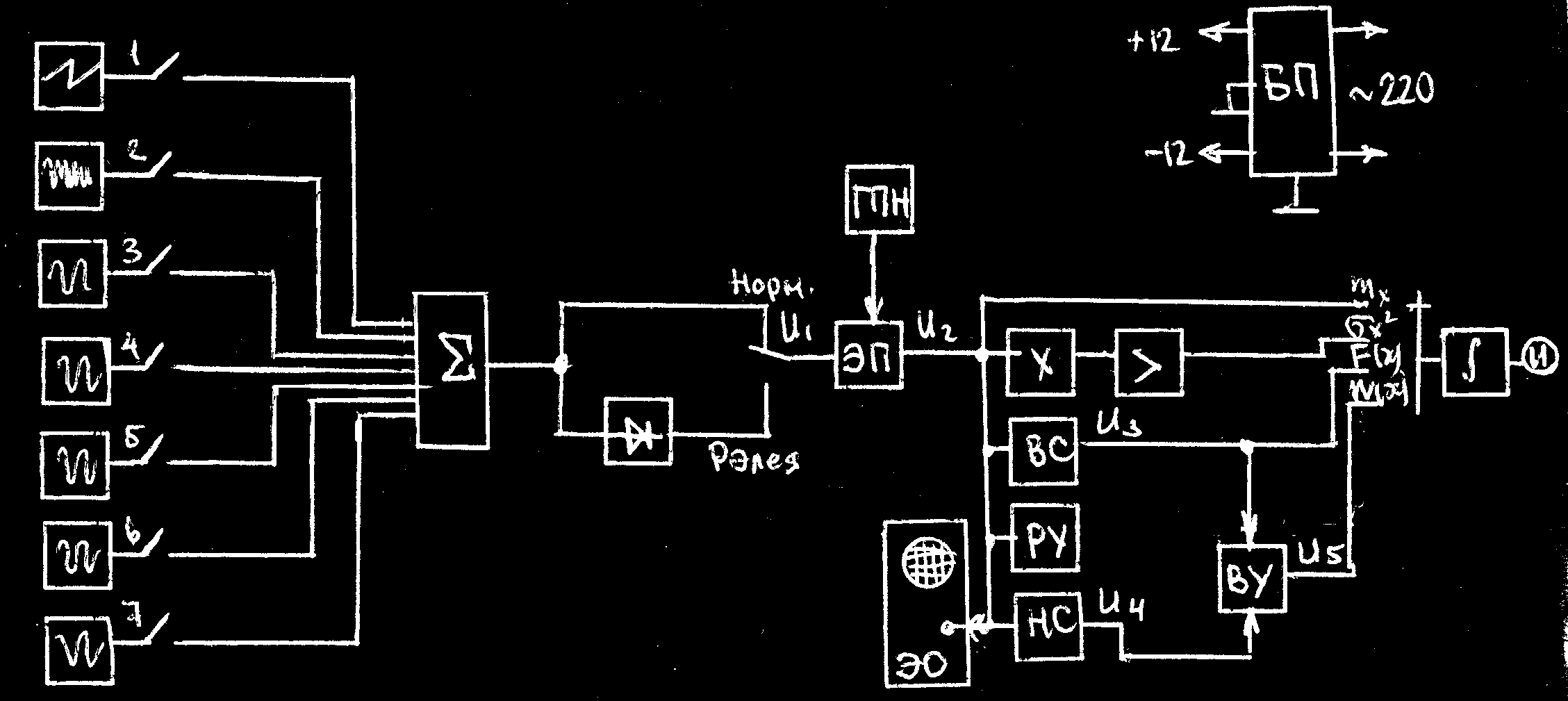
... функция и функция плотности и вероятности имеют следующий вид: Описание лабораторной установки Для выполнения работы необходимо использовать универсальный стенд для изучения законов распределения случайных процессов и электронный осциллограф. Передняя панель стенда Стенд включает в себя: - семь источников независимых случайных сигналов (одного шумового с нормальным распределением, ...
... ≠ j) X(t) = mx(t) + ∑ Viφi(t) (t ? T) Следует: K(t, t’) = ∑ Diφi(t)φi(t’) Эту формулу называют каноническим разложением корреляционной функции случайного процесса. В случае уравнения X(t) = mx(t) + ∑ Viφi(t) (t ? T) Имеют место формулы: X(t) = mx(t) + ∑ Viφ(t) ∫ x(τ)dt = ∫ mx(τ)dτ + ∑ Vi ...
... и реализация оптимальных в определенном смысле свойств системы по заданным статистическим свойствам входных сигналов. Статистическая динамика является разделом теории управления и базируется на теории вероятности и, в частности, на ее разделе теории случайных процессов. 1.1 Основные понятия теории вероятности Рассмотрим случайные величины и их характеристики. Случайное событие – это событие ...
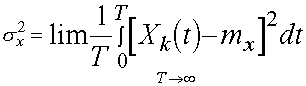
0 комментариев