Навигация
2. Теорема Лагранжа
Результаты теоремы Ролля используются при рассмотрении следующей теоремы о среднем, принадлежащей Лагранжу (1736–1813).
Теорема. Если функция 
непрерывна на отрезке 
и дифференцируема во всех его внутренних точках, то существует, по крайней мере, одна точка 
, в которой 
.
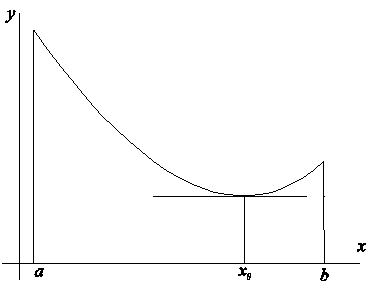
Доказательство. Рассмотрим график функции (рис. 2.1).
Проведем хорду, соединяющую точки 
и 
, и запишем ее уравнение. Воспользовавшись уравнением прямой, проходящей через две точки на плоскости, получим:
,
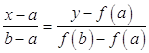откуда:
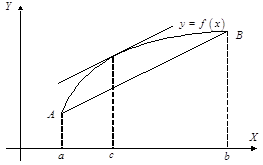
Рис. 2.1
и 
.
Составим теперь вспомогательную функцию, вычтя из уравнения кривой уравнение хорды:
.
Полученная функция 
непрерывна на отрезке и дифференцируема во всех его внутренних точках. Кроме того, вычисление в точках 
и 
показывает, что 
. Значит, функция на отрезке 
удовлетворяет требованиям теоремы Ролля. Но в этом случае существует такая точка , в которой 
.
Вычислим производную функции :
.
Согласно теореме Ролля в точке 
производная , то есть 
и
,
что и требовалось доказать.
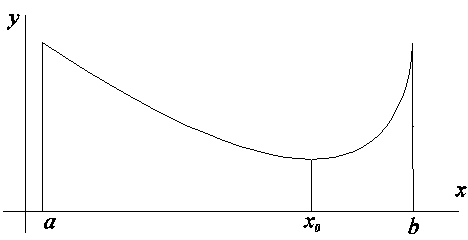
Геометрический смысл теоремы Лагранжа следующий: внутри отрезка существует, по крайней мере, одна точка, в которой касательная параллельна хорде, стягивающей кривую на данном отрезке. В частности, при 
теорема переходит в теорему Ролля.
Теорему Лагранжа часто записывают в следующем виде:
,
то есть приращение функции равно приращению аргумента, умноженному на производную функции в некоторой внутренней точке. В связи с этим теорему Лагранжа называют также теоремой о конечных приращениях.
3. Теорема Коши
Рассмотрим, наконец, третью теорему о среднем, принадлежащей Коши (1789–1859), которая является обобщением теоремы Лагранжа.
Теорема. Если функции 
и 
непрерывны на отрезке и дифференцируемы во всех его внутренних точках, причем 
не обращается в ноль ни в одной из указанных точек, то существует, по крайней мере, одна точка , в которой 
.
Доказательство. Так как 
во всех точках 
, то отсюда следует, что 
. В противном случае, как следует из теоремы Ролля, существовала хотя бы одна точка , в которой 
.
Составим вспомогательную функцию
.
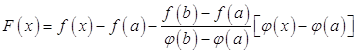Данная функция непрерывна на отрезке и дифференцируема во всех его внутренних точках. Кроме того, вычисление ее в точках и дает: . Значит, функция удовлетворяет требованиям теоремы Ролля, то есть существует хотя бы одна точка , в которой .
Вычислим производную :
.
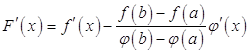Из условия следует, что
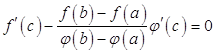и ,
что и требовалось доказать.
В случае, когда 
, теорема Коши переходит в формулировку теоремы Лагранжа.
Похожие работы
... типов неопределенностей. Примеры для этого и последующего раздела были взяты из [Марон]. В четвертом разделе приведен вывод формулы Тейлора и показано применение формулы Тейлора для нахождения эквивалентных функций и вычисления пределов. 1. Бесконечно малые и их сравнения; символы "o малое" и "о большое" Определение. Бесконечно малой в x0 называется функция f (x) такая, что Свойства ...
рема Ферма: Если функция у=f(х) имеет в точке х0 локальный экстремум и дифференцируема в этой точке, то ее производная f'(х0) равна нулю. Док-во: Проведем его для случая максимума в точке х0. Пусть (х0-d, х0+d) - та окрестность, для точек которой выполняется неравенство Здесь возможно как 1 и 2 варианты, но | ∆х| <δ При ∆х>0, будет ∆y:∆x ...
... и докажите сходимость полученного разложения к порождающей функции. Исследовать на абсолютную и условную сходимость . Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЙ АНАЛИЗ Билет № 12 Сформулируйте теорему Ролля и объясните ее геометрический смысл. Исследуйте функцию на выпуклость и вогнутость. Какая ...
... вытекает, что f'(c)=0. #30 Теорема (Ролля). Если функция y=f(x) непрерывна на [а, b], дифференцируема на (а, b) и f (а) ==f(b), то существует точка c0(а,b), такая, что f'(c)=0. Доказательство. Если f постоянна на [а, b], то для всех c(a, b) производная f'(c)=0. Будем теперь считать, что f непостоянна на [а, b]. Так как f непрерывна на [а, b], то существует точка x1 [а, ...
0 комментариев