Навигация
Шпоры по математическому анализу
1. Производные и дифференциалы высших порядков
Опр-ие: производной n-го порядка (n³2) функции у=f(х) называется производная (первого порядка) от производной (n-1)-го порядка.
Найдя 1-ю производную можно определить 2-ю производную по тем же формулам, по которым определяли первую.
Опр-ие: Дифференциалом n-го порядка функции у=f(х) называется дифференциал первого порядка от дифференциала (n-1)-го порядка. (обозначается dny)По определению dny= d(dn-1y). Иногда dy называют диф. Первого порядка. В общем случае, dny=f(n)(х)dxn, в предположении, что n-ая производная f(n)(х) сущ-ет, поэтому понятно, что n-e. Производную обозначают так
3. Теорема Ролля.
Теорема Ролля: Если функция у=f(х) непрерывна на замкнутом промежутке [a,b], дифференцируема хотя бы в открытом промежутке (a,b) и на концах промежутка ее значения совпадают f(a)=f(b), то внутри промежутка найдется такая точка x=c, что f'(c)=0
Док-во: Если функция сохраняет постоянное значение на промежутке [a,b], f(х)= f(a)=f(b), то f'(c)=0 и в качестве точки с можно взять любую точку интервала (a,b).
Пусть теперь функция f(x) не является постоянной. По теореме Вейштраса существуют точки х1 и х2 на отрезке [a,b] , в которых достигаются наименьшее m и наибольшее М значения функции. Обе эти точки не могут быть концевыми для отрезка [a,b], т.к. из условия f(a)=f(b) вытекало бы, что m=М, следовательно, функция f(х) сохраняла бы постоянное значение, вопреки предположению.
Допустим, что не совпадает с концом отрезка точка х1, т.е. a< х1<b, тогда х1 является точкой локальности экстремума. По условия теоремы существует f'(х1). Из этих двух утверждений по теореме Ферма получаем f'(х1)=0, следовательно,
х1 можно принять за точку с.
2. Теорема Ферма (необходимое условие локального экстремума).
Опр-ие: Функция у=f(х) имеет в точке x0локальный максимум, если сущ-ет окрестность (х0-d, х0+d), для всех точек х которой выполняется неравенство f(х)£f(х0). Аналогично определяется локальный минимум, но выполняться должно равенство f(х)³f(х0).
![]()
Теорема Ферма: Если функция у=f(х) имеет в точке х0 локальный экстремум и дифференцируема в этой точке, то ее производная f'(х0) равна нулю.
Док-во: Проведем его для случая максимума в точке х0. Пусть (х0-d, х0+d) - та окрестность, для точек которой выполняется неравенство
Здесь возможно как 1 и 2 варианты, но | ∆х| <δ
При ∆х>0, будет ∆y:∆x ≤0, поэтому
При ∆х<0, будет ∆y:∆x ≥0, поэтому
По условию теоремы, существует производная f'(х0)А это означает, что правая производная fпр'(х0) и левая производная fл'(х0) равны между собой: fпр'(х0)= fл'(х0)= f'(х0). Таким образом, с одной стороны, f'(х0)≤0, с другой стороны, f'(х0)≥0, что возможно лишь, когда f'(х0)=0.
4. Теорема Коши.
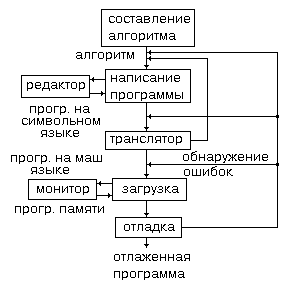
Теорема Коши: Пусть функции у=f(х) и у=g(х) неперырвны на отрезке [a,b],дифференцируемы хотя бы в открытом промежутке (a,b) и на этом промежутке g'(х) не обращается в нуль. Тогда существует такая точка c Î (a,b), что выполняется равенство (1)
Докозательство: Вначале отметим, что знаменатель g(b)-g(a) ≠ 0,т.к. из равенства g(b)=g(a) следовало бы по теореме Ролля, что производная g'(х) обратилась бы в нуль в какой-нибудь точке промежутка (a,b), что противоречит условию g'(х)≠0. Образуем вспомогательную функцию:
К ней применима теорема Ролля: F(х) непрерывна в [a,b] и дифференцируема в (a,b) как сумма функций, непрерывных и дифференцируемых в соответствующих промежутках, кроме того, как легко проверить непосредственно, F(a)=F(b)=0. Следовательно, существует точка c Î (a,b), , такая, что F'(c)=0. Вычисляем:
![]()
Подставляем x=c:
После деления на g'(х) (причем как говорилось раньше g'(х) ¹0), мы приходим к формуле (1)
5. Теорема Лагранжа.
Теорема Лагранжа: Если функция у=f(х) неперырвна на отрезке [a,b], дифференцируема хотя бы в интервале (a,b) то существует такая точка c Î (a,b), что f(b)-f(a)=f'(c)(b-a).
Доказательство: Применим теорему Коши к функциям f(x) и g(x)=x. Для них все условия этой теоремы выполняются, включая требование g'(х)¹0. Учитывая, что g(b)=b, g(a)=a, g'(x)=1, получим, (2)
Где точка с-точка, существующая в силу теоремы Коши в интервале (a,b). Умножив обе части на b-a, придем к формуле (2).
6. Правило Лопиталя.
Пусть выполнены следующие условия:
1. Функции f(x) и g(x) определены и дифференцируемы в выколотой окрестности точки a.
2. (1)
3. g(x) и f(x) не равны нулю в этой выколотой окрестности.
Если при этом существует (2)
![]()
То существует и (3)
Причем, они равны между собой.(4)
![]()
Доказательство: Доопределим функции f(x) и g(x) в точке x=a, положив f(a)=g(a)=0. Рассмотрим отрезок между числами a и x, где точка из упомянутой в условии выколотой окрестности. Для определенности будем считать, что x<a. Обе функции на отрезке [x,a] неперывны, а в интервале (x,a) дифференцируемы, т.е. удовлетворяют условиям теоремы Коши. Следовательно, Существует такая точка сÎ(x,a), что выполняется равенство(5)
![]()
Так как f(a)=g(a)=0. При х®а будет с®а, потому x<c<a.
По условию теоремы существует (2). Здесь х можно заменить любой другой буквой, в частности с. Переходя к пределу в равенстве (5) при х®а, получим
![]()
Или, что то же самое (4).
Похожие работы
... нельзя быть аморальным политиком. Средство борьбы против этого --- гласность. Ход исторического процесса --- антагонизм. b 10---------- 1. Теоретическое и обыденное сознание. Знание и мнение в древнегреческой философии. Акцент делать на этом вопросе. Общественное сознание - духовная, идеологическая жизнь общества, его мировозрение. Общественное сознание формируется и развивается вместе ...
... . — С 73-77. Лосев А. Ф. Типы античного мышления // Античность как тип культуры. — М., 1988. — С. 78-104. Луканин Р. К. Из истории античного опыта и эксперимента // Филос. науки. — 1991. — № 11. — С. 23-36. Луканин Р. К. Категории Аристотеля в истолковании западноевропейских философов // Путем Октября. — Махачкала, 1990. — С. 84-103. Луканин Р. К. "Среднее"— специфическое понятие аттической ...
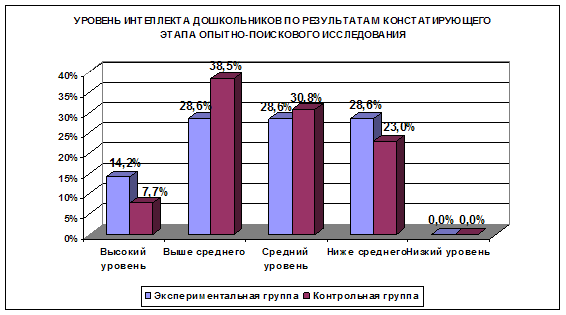
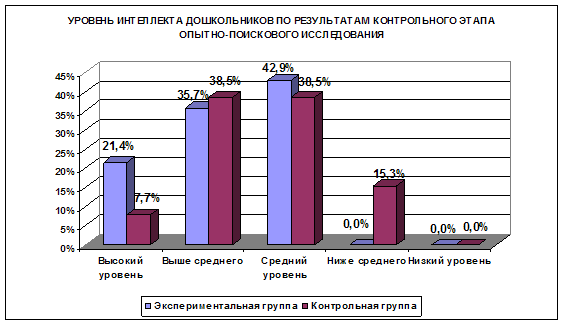
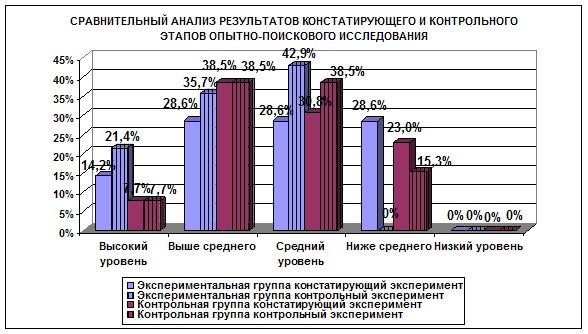
... то целесообразно разработать комплекс заданий по развитию интеллектуальных способностей дошкольников и внедрить его в математический блок программы «Радуга». 2.2 Опытно-поисковые исследования по развитию интеллектуальных способностей средствами математики Для проверки выдвинутой гипотезы провели опытно-поисковые исследования. Опытно-поисковые исследования состояли из трех этапов. На первом ...
... руководителя. Большое внимание следует уделять мотивации управленческого труда. 56. Организационно-распорядительные методы управления (Или административные). С их помощью осуществляются регулирующие функции гос-ва. Основаны на исполнении обязательных предписаний и рекомендаций, позволяют оперативно воздействовать на ход событий в процессе упр-я, ср-во волевого и конкретного воздействия ( ...



0 комментариев