Навигация
4. Правило Лопиталя
На основании теоремы Коши о среднем можно получить удобный метод вычисления некоторых пределов, называемый правилом Лопиталя (1661–1704).
Теорема. Пусть функции 
и 
непрерывны и дифференцируемы во всех точках полуинтервала 
и при 
совместно стремятся к нулю или бесконечности. Тогда, если отношение их производных имеет предел при , то этот же предел имеет отношение и самих функций, то есть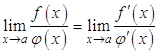 
.
Проведем доказательство данной теоремы только для случая, когда 
. Так как пределы у обеих функций одинаковы, то доопределим их на отрезке 
, положив, что при 
выполняется равенство 
.
Возьмем точку 
. Так как функции и удовлетворяют теореме Коши (п. 2.14), применим ее на отрезке 
:
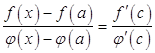, где 
.
Так как , то
.
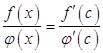Перейдем в данном равенстве к пределу:
.
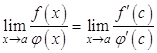Но если , то и 
, находящееся между точками 
и 
, будет стремится к , значит
.
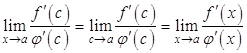Отсюда, если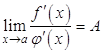 
, то и 
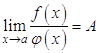, то есть
,
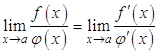что и требовалось доказать.
Если при 
, то снова получается неопределенность вида 
и правило Лопиталя можно применять снова, то есть
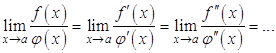
Доказательство правила Лопиталя для случая 
проводится сложнее, и мы его рассматривать не будем.
При раскрытии неопределенностей типа 
, 
, 
, 
, 
правило Лопиталя применять непосредственно нельзя. Вначале все эти неопределенности необходимо преобразовать к виду или .
Правило Лопиталя может быть использовано при сравнении роста функций, в случае когда 
. Наибольший практический интерес здесь представляют функции 
, 
, 
. Для этого найдем пределы их отношений:
1) 
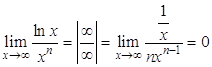, значит, растет быстрее, чем ;
2) 
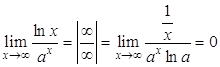, значит, растет быстрее, чем ;
3) 
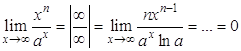, значит, растет быстрее, чем .
Отсюда следует, что быстрее всего растет , затем и, наконец, .
Литература
1. Гмурман В.Е. Теория вероятностей и математическая статистика. М., «Высшая школа» изд. 5, 1977.
2. Зайцев И.А. Высшая математика. ДРОФА, 2005. – 400 с.
3. Краснов М. Вся высшая математика т. 1 изд. 2. Едиториал УРСС, 2003. – 328 с.
4. Краснов М.Л., Макаренко Г.И., Киселев А.И., Шикин Е.В. Вся высшая математика Интегральное исчисление. Дифференциальное исчисление функций нескольких переменных. Дифференциальная геометрия Том 2.: Учебник – 3-е изд. ЛКИ, 2007.
5. Мироненко Е.С. Высшая математика. М: Высшая школа, 2002. – 109 с.
Похожие работы
... типов неопределенностей. Примеры для этого и последующего раздела были взяты из [Марон]. В четвертом разделе приведен вывод формулы Тейлора и показано применение формулы Тейлора для нахождения эквивалентных функций и вычисления пределов. 1. Бесконечно малые и их сравнения; символы "o малое" и "о большое" Определение. Бесконечно малой в x0 называется функция f (x) такая, что Свойства ...
рема Ферма: Если функция у=f(х) имеет в точке х0 локальный экстремум и дифференцируема в этой точке, то ее производная f'(х0) равна нулю. Док-во: Проведем его для случая максимума в точке х0. Пусть (х0-d, х0+d) - та окрестность, для точек которой выполняется неравенство Здесь возможно как 1 и 2 варианты, но | ∆х| <δ При ∆х>0, будет ∆y:∆x ...
... и докажите сходимость полученного разложения к порождающей функции. Исследовать на абсолютную и условную сходимость . Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЙ АНАЛИЗ Билет № 12 Сформулируйте теорему Ролля и объясните ее геометрический смысл. Исследуйте функцию на выпуклость и вогнутость. Какая ...
... вытекает, что f'(c)=0. #30 Теорема (Ролля). Если функция y=f(x) непрерывна на [а, b], дифференцируема на (а, b) и f (а) ==f(b), то существует точка c0(а,b), такая, что f'(c)=0. Доказательство. Если f постоянна на [а, b], то для всех c(a, b) производная f'(c)=0. Будем теперь считать, что f непостоянна на [а, b]. Так как f непрерывна на [а, b], то существует точка x1 [а, ...
0 комментариев