Кривая определяется как линия пересечения данной поверхности плоскостью, положение которой определено
Кривая определяется как линия, получаемая в результате того или иного геометрического преобразования уже известной кривой
Точка О (0; 0) принадлежит эллипсу;
Взяв на плоскости прямоугольную декартову систему координат, изобразить области, определяемые следующими системами неравенств
Навигация
Кривая определяется как линия пересечения данной поверхности плоскостью, положение которой определено
Плоские кривые
57781
знак
2
таблицы
39
изображений
1. Кривая определяется как линия пересечения данной поверхности плоскостью, положение которой определено.
В истории развития учения о кривых этот способ является первым. Греки определяли кривые второго порядка как сечения кругового конуса. Таково же происхождение кривых Персея, получаемых в результате сечений плоскостью поверхности тора. Эвольвента круга может быть определена как линия пересечения поверхности касательных к винтовой линии, перпендикулярной к её оси и т.д.
2. Кривая определяется как геометрическое место точек, обладающих данным свойством.
Этот способ особенно употребителен. Он широко практиковался ещё греческими математиками; так Евклид рассматривал конические сечения как геометрические места точек, сохраняющих постоянное отношение расстояний от данной точки и от данной прямой. Как геометрическое место точек была определена Диоклесом его циссоида. Таким же способом определяет Никомед конхоиду. Такие линии, как овалы Декарта, овалы Кассини, улитка Паскаля, строфоида, верзиера и целый ряд других кривых, определяются обычно как геометрические места.
3. Кривая определяется как траектория точки, характер движения которой обусловлен тем или иным образом.
Кинематический способ образования линий был также хорошо известен греческим учёным. Как траекторию точки, участвующей одновременно в двух равномерных движениях, одно из которых совершается по прямой, а другое – по окружности, определил Архимед свою спираль. Все циклоидальные кривые являются траекториями точки, жёстко связанной с кругом, который катится без скольжения по окружности другого круга. Кинематическим путём определяется квадратриса Динострата как траектория точки пересечения вращающегося радиуса окружности с хордой, двигающейся параллельно самой себе. Лемниската Бернулли может быть определена как траектория середины большого звена шарнирного антипараллелограмма, противоположное звено которого закреплено. Кинематически определяются розы, кривые скольжения и многие другие линии. Кинематический способ задания кривой полагался Декартом в основу определения кривых методом координат.
4. Образование линий по способу сопряжения проективно соответствующих элементов.
Этот способ сравнительно недавнего происхождения и во всей полноте рассматривается в курсах проективной геометрии. В основу его полагается идея соответствия двух проективных рядов точек или двух проективных пучков.
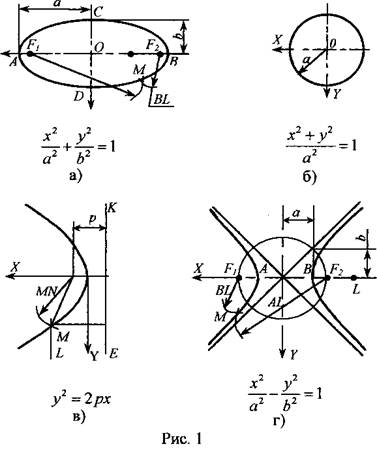
Проективно соответствующими называются два прямолинейных ряда точек, если любым четырём гармоническим точкам одного из них соответствуют также четыре гармонические точки второго ряда. Аналогично определяется проективное соответствие пучков прямых. На основе этих понятий и возникает проективный способ образования линий. Так, если имеюся два проективных пучка прямых, то геометрическое место точек пересечения соответствующих прямых этих пучков представляет собой кривую второго порядка (рис. 1, а).
Точно так же, если заданы два проективно связанных прямолинейных ряда точек, то огибающая прямых, проходящих через соответствующие точки этих рядов, будет представлять собой кривую второго класса и одновременно второго порядка (рис. 1, б).
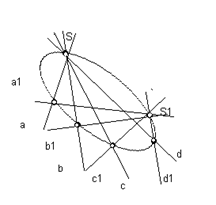Рис. 1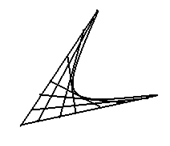
На кривой второго порядка могут быть в свою очередь определены гармонические четвёрки точек, т.е. точки пересечения этой кривой с четырьмя гармонически сопряжёнными лучами пучка прямых, центр которого находится в какой-либо точке этой кривой. Так возникает понятие криволинейного проективного ряда, который в отличие от прямолинейного ряда называется проективным рядом второго порядка. Аналогично устанавливается понятие пучка второго порядка, под которым понимают упомянутую выше совокупность прямых, проходящих через соответствующие точки двух прямолинейных проективных рядов и огибающих кривую второго порядка.
Понятие ряда второго порядка и пучка второго порядка позволяет определить проективным способом алгебраические кривые высших порядков и классов.
Частным случаем проективного соответствия является перспективное соответствие, которое осуществляется путём проектирования двух плоских систем из общего центра. Соответствующие точки при этом лежат на одном проектирующем луче. а соответствующие прямые принадлежат одной пректирующей плоскости.
Способом проектирования могут быть получены многие из часто встречающихся кривых. Сюда относится циклоида, являющаяся параллельной проекцией винтовой линии на плоскость, параллельную её оси. Спираль Архимеда может быть определена как проекция конической винтовой линии на плоскость, перпендикулярную её оси. Овалы Декарта могут быть определены как проекции линии пересечения двух конических поверхностей с параллельными осями на плоскость, перпендикулярную к этим осям, и т.д.
5. Кривая определяется заданием её дифференциальных свойств.
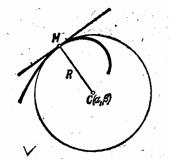
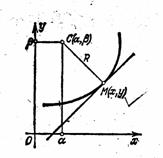
Непосредственно задаваемое по условию задачи или вытекающее из этого условия соотношение между бесконечно малыми элементами кривой выражается сначала в виде некоторого дифференциального уравнения. Последующее интегрирование этого уравнения приводит к обычному уравнению искомой кривой. Такой способ определения уравнения кривой характерен для многочисленных задач геометрии, механики, физики, техники. Так показательная кривая может быть определена как линия, у которой подкасательная для всех точек имеет одно и то же значение. Трактриса характеризуется постоянством длины касательной. Радиоидальная спираль определяется как линия, для которой радиус кривизны обратно пропорционален длине дуги. На основании геометрических соображений и законов механики выводятся дифференциальные уравнения цепной линии, изогнутой оси балки и т.д.
Похожие работы
... можно показать, что формулы будут справедливы и в случае y!!<0. Параметрическое задание кривой Если кривая задана параметрически: x = j(t), y = y(t), то координаты центра кривизны можно получить из формул *, подставляя в них вместо y! и y!! их выражения через параметр: . Тогда (2) Эволюта и эвольвента Если в точке M1(x, y) данной линии кривизна отлична от нуля, то этой точке соответствует ...
... і координат , Матимемо (10.12) Пропонується вивести цю формулу, узявши до уваги, що рівняння кривої в полярних координатах можна записати як параметричні з параметром q : і використавши формулу (10.10). Приклад 1. Обчислити довжину кривої, заданої рівнянням Розв‘язок. Досить обчислити довжину дуги, що обмежує зверху заштриховану на рис.10.7 фігуру, а потім помножити її на ...
... дуги. Спиралями являются также эвольвенты замкнутых кривых, например эвольвента окружности. Названия некоторым спиралям даны по сходству их полярных уравнений с уравнениями кривых в декартовых координатах, например: · параболическая спираль (а - r)2 = bj, · гиперболическая спираль: r = а/j. · Жезл: r2 = a/j · si-ci-cпираль, параметрические уравнения которой имеют вид: , [si (t) и ci ...
... закону. Эту линию называют образующей. Она может быть прямой, и тогда образованную ею поверхность относят к классу линейчатых. Если образующая - кривая линия, поверхность считают нелинейчатой. Линию, по которой перемещают образующую, называют направляющей. В качестве последней иногда используют след поверхности, т. е. линию ее пересечения с плоскостью проекций. Определителем поверхности называют ...
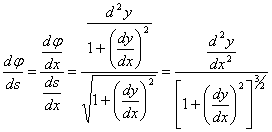
0 комментариев