Навигация
3. ПОДОБИЕ ФИГУР
Две фигуры называются подобными, если они переводятся друг в друга преобразованием подобия. Для обозначения подобия фигур используется специальный значок: ∞. Запись F∞F' читается так: «Фигура F подобна фигуре F'».
Докажем, что если фигура F1 подобна фигуре F2, а фигура F2 подобна фигуре F3, то фигуры F1 и F3 подобны.
Пусть Х1 и Y1 — две произвольные точки фигуры F1. Преобразование подобия, переводящее фигуру F1 в F2, переводит эти точки в точки Х2, Y2, для которых X2Y2 = k1X1Y1.
Преобразование подобия, переводящее фигуру F2 в F3, переводит точки Х2, Y2 в точки Х3, Y3, для которых X3Y3 = - k2X2Y2.
Из равенств
X2Y2=kX1Y1, X3Y3 = k2X2Y2
следует, что X3Y3 - k1k2X1Y1. А это значит, что преобразование фигуры F1 в F3, получающееся при последовательном выполнении двух преобразований подобия, есть подобие. Следовательно, фигуры F1 и F3 подобны, что и требовалось доказать.
В записи подобия треугольников: ΔABC∞ΔA1B1C1 — предполагается, что вершины, совмещаемые преобразованием подобия, стоят на соответствующих местах, т. е. А переходит в А1, В - в B1 и С - в С1.
Из свойств преобразования подобия следует, что у подобных фигур соответствующие углы равны, а соответствующие отрезки пропорциональны. В частности, у подобных треугольников ABC и А1В1С1
A=
А1, В=В1, С=С1
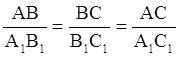
4. ПРИЗНАК ПОДОБИЯ ТРЕУГОЛЬНИКОВ ПО ДВУМ УГЛАМ
Теорема 2. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
Доказательство. Пусть у треугольников ABC и A1B1C1 А=А1, B=B1. Докажем, что ΔАВС~ΔА1В1С1.
Пусть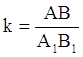 
. Подвергнем треугольник А1В1С1 преобразованию подобия с коэффициентом подобия k, например гомотетии (рис. 6). При этом получим некоторый треугольник А2В2С2, равный треугольнику ABC. Действительно, так как преобразование подобия сохраняет углы, то A2=А1, B2= B1. А значит, у треугольников ABC и А2В2С2A = A2, B=B2. Далее, A2B2 = kA1B1=AB. Следовательно, треугольники ABC и А2В2С2 равны по второму признаку (по стороне и прилежащим к ней углам).
Так как треугольники А1В1С1 и А2В2С2 гомотетичны и, значит, подобны, а треугольники А2В2С2 и ABC равны и поэтому тоже подобны, то треугольники А1В1С1 и ABC подобны. Теорема доказана.
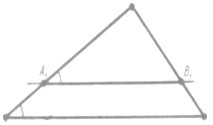
Рис. 7
Задача. Прямая, параллельная стороне АВ треугольника ABC, пересекает его сторону АС в точке А1, а сторону ВС в точке В1. Докажите, что Δ ABC ~ ΔА1В1С.
Решение (рис. 7). У треугольников ABC и А1В1С угол при вершине С общий, а углы СА1В1 и CAB равны как соответствующие углы параллельных АВ и А1В1 с секущей АС. Следовательно, ΔАВС~ΔА1В1С по двум углам.
Похожие работы
... - медианы треугольников; 4. , , где BH и B1H1 высоты треугольников. §5. Опытная работа Цель опытной работы: выявление методических особенностей изучения темы «Подобные треугольники» в средней школе. Идея: для выявления методических особенностей необходимо провести несколько уроков по разработанной методики, в конце обучения провести контрольную работу, при анализе которой можно судить о ...
... . Позитивизма. Для позитивистов верным и испытанным является только то, что получено с помощью количественных методов. Признают наукой лишь математику и естествознание, а обществознание относят к области мифологии. Неопозитивизм, Слабость педагогики неопозитивисты усматривают в том, что в ней доминируют бесполезные идеи и абстракции, а не реальные факты. Яркий ...
... учебник и задачник / А. П. Кисилев, Н.А. Рыбкин. – М.: Дрофа, 1995. 9. Изучение личности школьника / под. ред. Л.И. Белозеровой. – Киров, Информационный центр, 1991. 10. Коновалова, В.С. Решение задач на построение в курсе геометрии как средство развития логического мышления / В.С. Коновалова, З.В. Шилова // Познание процессов обучения физике: сборник статей. Вып.9. – Киров: Изд-во ...
... развитие логического мышления учащихся является одной из основных целей курса геометрии. При изучении геометрии развитие логического мышления учащихся осуществляется в процессе формирования понятий, доказательства теорем, решения задач. При изучении геометрических построений, прежде всего, приходится преодолевать трудности логического порядка. В условиях школы для преодоления этих трудностей ...
0 комментариев