Навигация
S – дистрибутивная решетка
1. S – дистрибутивная решетка.
2. ![]()
Доказательство.
![]() . Очевидно.
. Очевидно.
![]() . По свойству 2 следует
. По свойству 2 следует ![]() , тогда:
, тогда:
![]() и
и ![]() .
.
Эти условия наряду с ассоциативностью, коммутативностью и идемпотентными законами определяют дистрибутивную решетку.
V. В ограниченном полукольце единица 1 – единственный обратимый элемент.
Доказательство.
Пусть есть некоторый обратимый элемент u,
![]() и
и ![]()
![]()
VI. Пусть a – фиксированный элемент полукольца S, тогда каждое из утверждений влечет следующее утверждение:
1. a+1=1;
2. ![]()
![]()
3. ![]()
![]()
Доказательство.
![]() . Докажем методом математической
индукции по числу n.
. Докажем методом математической
индукции по числу n.
I. База. к=1. ![]() (выполняется по условию).
(выполняется по условию).
II. Индуктивное предположение. Пусть для к<n условие выполняется, т.е.![]()
Рассмотрим для k=n
![]() и a+1=1
и a+1=1 ![]()
![]()
Из I и II Следует ![]() .
.
![]() .
. ![]() .
.
Можно выбрать из всего количества N, некоторое число, для которого тоже данное выражение будет верно.
Примером того , что условие 3 не влечет условие 1 является полукольцо матриц ![]() . Зафиксируем элемент
. Зафиксируем элемент ![]() , где
, где ![]() . Для n=2
. Для n=2
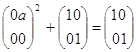 верно, но
верно, но ![]() совсем неверно.
совсем неверно.
VII. Если S – полукольцо с мультипликативным сокращением и аддитивно идемпотентно, то все утверждения предыдущего свойства равносильны.
Доказательство.
Осталось доказать ![]() .
.
Имеем ![]() . Добавим к правой и левой части выражения равные элементы
. Добавим к правой и левой части выражения равные элементы ![]() :
:
![]()
В силу аддитивной идемпотентности мы можем подбирать коэффициенты перед ![]() . В соответствии с биномом Ньютона, подберем коэффициенты и получим:
. В соответствии с биномом Ньютона, подберем коэффициенты и получим:
![]()
Используя мультипликативную сократимость, получим a+1=1. Что и доказывает равносильность условий 1 – 3.
VIII. Пусть S – ограниченное полукольцо, и существует такое ![]() , что
, что ![]() для всех
для всех ![]() . Тогда:
. Тогда:
1. ![]() для всех
для всех ![]() ;
;
2. ![]() - коммутативное ограниченное полукольцо с 1, где I – множество всех мультипликативных идемпотентов из S, а операция
- коммутативное ограниченное полукольцо с 1, где I – множество всех мультипликативных идемпотентов из S, а операция![]() определяется так:
определяется так:
![]() .
.
Доказательство.
1. Возьмем ![]() .
.
Тогда ![]() , т.к.
, т.к. ![]() .
.
Для доказательства понадобится
Лемма: В ограниченном полукольце
![]() .
.
Доказательство: ММИ по числу n в ![]() .
.
I. База. n=1. Из условия ограниченности
![]()
![]()
II. И.П. n=i-1.
![]()
Из условия II и ограниченности:
![]()
![]()
![]() .
.
По ИП:
![]()
Из условий I,II получили, что данное равенство верно для ![]() , лемма доказана.
, лемма доказана.
Рассмотрим ![]() :
:
![]()
Поскольку степень равна 2n-1, то в каждом из составляющих сумму слагаемых, либо![]() (1 группа), либо
(1 группа), либо ![]() (2 группа), и только так.
(2 группа), и только так.
Среди слагаемых 1 группы имеется член ![]() . Этот член в сумме с каждым слагаемым 1 группы будет давать самого себя, при условии
. Этот член в сумме с каждым слагаемым 1 группы будет давать самого себя, при условии ![]() и лемме 1. из группы 1 останется только элемент
и лемме 1. из группы 1 останется только элемент ![]()
Аналогично с элементами группы 2, в которой имеется элемент ![]() , который и останется. Получаем
, который и останется. Получаем
![]()
2 .Прежде всего проверим замкнутость операций ![]() и + на множестве I.
и + на множестве I.
![]()
![]()
![]()
(1) Поскольку в качестве аддитивной операции выбрано сложение, и все элементы из полукольца, значит (I,+) – коммутативная полугруппа с нейтральным элементом 0.
(2) Докажем, что ![]() - коммутативная полугруппа с нейтральным элементом 1:
- коммутативная полугруппа с нейтральным элементом 1:
a). Ассоциативность:
Рассмотрим элемент ![]()
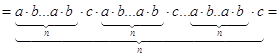
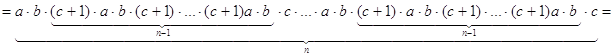
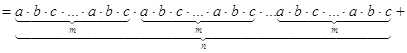

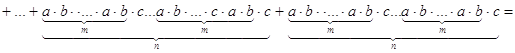
![]()
Элемент X состоит из таких слагаемых, которые получены при умножении, кроме тех которые получены при произведении со всеми 1, или со всеми с. Элемент ![]() имеется в качестве сомножителя в каждом слагаемом X, т.е.
имеется в качестве сомножителя в каждом слагаемом X, т.е.
![]()
![]()
![]()
С другой стороны ![]()
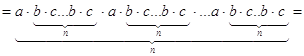
![]()

![]()
Таким образом, правые части рассматриваемых тождеств равны, значит ассоциативность доказана. ![]()
b). 1 – нейтральный элемент:
![]()
с). Коммутативность:
![]() ,
, ![]()
1.![]()
![]()
2.![]()
![]()
Из 1 и 2 следует ![]() , по причине равенств правых частей каждого, а значит следует равенство
, по причине равенств правых частей каждого, а значит следует равенство ![]() . Коммутативность доказана.
. Коммутативность доказана. ![]() - коммутативная полугруппа с нейтральным элементом 1.
- коммутативная полугруппа с нейтральным элементом 1.
(3) Дистрибутивность:
![]()
![]()
(4) ![]()
Все аксиомы полукольца доказаны, а значит ![]() - коммутативное полукольцо и его элементы – элементы ограниченного полукольца, значит полукольцо – ограничено.
- коммутативное полукольцо и его элементы – элементы ограниченного полукольца, значит полукольцо – ограничено.
IX. Если в положительном полукольце S выполняется равенство
![]()
![]() ,
,
то S – аддитивно идемпотентно.
Доказательство.
![]()
![]()
Рассмотрим t>1
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Рассмотрим t=1, ![]()
![]()
![]()
![]()
…
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
т.к. полукольцо положительно, то в обеих частях обратимые элементы, домножим на обратный и получим 1+1=1, умножим обе части на u, получим u+u=u, что и означает аддитивную идемпотентность.
X. В положительном полукольце S ![]() справедливо следующее тождество:
справедливо следующее тождество:
![]()
Доказательство.
![]()
Домножим на обратный к ![]() :
: ![]()
Получим:
![]()
Что и требовалось доказать.
Библиографический список
1. Чермных, В.В. Полукольца [Текст] / В.В. Чермных – Киров: Изд-во ВГПУ, 1997. – ст.7 – 87.
2. Вечтомов, Е.М. Введение в полукольца [Текст] / Е.М. Вечтомов – Киров: Издательство ВГ ПУ, 2000. – ст.5 - 30.
Похожие работы
... S с 1 изоморфно прямому произведению кольца и антикольца тогда и только тогда, когда его идеал R(S) имеет единичный элемент, коммутирующий с каждым элементом из S [1]. 3. Полукольцо S служит 0-расширением кольца с помощью полутела тогда и только тогда, когда идеал R(S) полульца S простой (т.е. abÎR(S) влечет aÎR(S) или bÎR(S)). 4. Для полукольца S с 1 фактор-полукольцо S/R(S) ...
... Фк = 365 × 24 = 8760 ч Номинальный фонд времени – это количество часов в году в соответствии с режимом работы без учета потерь. Так как термическое отделение высокотемпературного отжига анизотропной электротехнической стали работает непрерывно, то номинальный фонд равен полному календарному, то есть Фн = Фк = 8760 ч. Действительный фонд времени равен тому времени, которое может быть ...
... дела как нельзя лучше играла на руку вредителям». (Мордвинов А.Г. «Искусство в массы», 1930, №12. От редакции «Современная архитектура», 1930, №5, стр. 2—3). 4. Коммуна и человек. Жилые дома и клубы Теперь перейдем к конкретным постройкам в Москве 1920-х годов. В первую очередь надо было решать жилищную проблему. Жилищное строительство после нескольких лет разрухи и гражданской войны ...
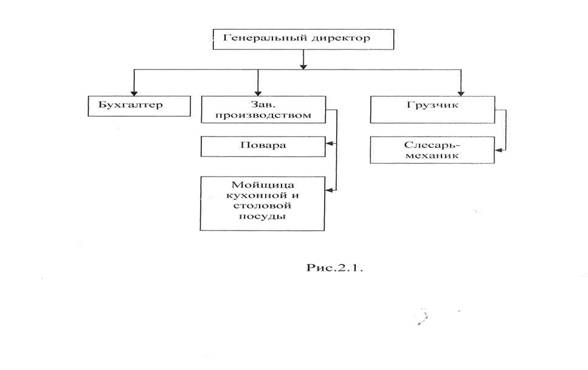
... и отпуска холодных блюд 10-14С; - повар обязательно следит за чистотой своего места. Отходы собираются в специальный отдельный бак и выносятся два раза в день. 3.4 Организация работы овощного цеха В столовой овощной цех находится рядом с кладовой овощей. Овощные полуфабрикаты поступают в горячий и холодный цеха, где и завершается выпуск готовой продукции. Технологический процесс ...
0 комментариев