Каждая фигура F конгруэнтна сама себе

1.         Каждая фигура F конгруэнтна сама себе.

Действительно, тождественное движение Н⁰ переводит F в F.

2.         Если фигура F₁ конгруэнтна F₂, то фигура F₂ конгруэнтна F₁.

В самом деле, если Н – движение, переводящее фигуру F₁ в F₂, то движение Н^-1 переводит фигуру F₂ в фигуру F₁.

3.         Если фигура F₁ конгруэнтна F₂, а фигура F₂ конгруэнтна фигуре F₃, то фигура F₁ конгруэнтна F₃.

Действительно, если Н' – движение, переводящее фигуру F₁ в F₂, а Н'' – движение, переводящее фигуру F₂ в F₃, то движение Н''Н' переводит F₁ в F₃.

Впервые подобную систему предложил спустя десять после появления гильбертовой аксиоматики Фридрих Шур.

Спустя ещё десять лет немецкий математик Герман Вейль (Weyl; 9.11.1885, Эльмсхорн, Шлезвиг-Гольштейн, – 8.12.1955, Цюрих) создал векторную аксиоматику геометрии. У Вейля первоначальными являются понятия «точка» и «вектор», а прямая и отрезок определяются с их помощью. Имеются аксиомы сложения векторов (означающие, что векторы образуют коммутативную группу), аксиомы умножения вектора на действительное число, аксиомы откладывания векторов (в частности, аксиома треугольника: ), аксиомы скалярного произведения векторов и аксиома размерности (для планиметрии в ней утверждается: если даны три ненулевых вектора ,  и , то какой-нибудь из них выражается в виде комбинации двух других: ). При заданных точке А и ненулевом векторе  прямая (А, ) определяется как множество всех точек М, для которых вектор пропорционален , то есть найдётся такое действительное число t, что . Далее определяются отрезки, углы, многоугольники, окружность и другие фигуры: например, расстояние между А и В – как квадратный корень из скалярного квадрата вектора , то есть . Теорема Пифагора легко доказывается с помощью скалярного произведения, а аксиома параллельности – с помощью векторного определения прямой и аксиомы разномерности.

В заключение отметим, что гильбертова аксиоматика полностью уточнила не вполне совершенную систему аксиом, созданную Евклидом более двух тысяч лет тому назад. Аксиоматика Фридриха Шура и аксиоматика Германа Вейля связали геометрию с понятиями группы преобразований и векторного пространства, которые играют важнейшую роль во многих разделах современной математики, физики, экономики, химии, биологии и других областей знания.

Глава II. Неевклидовы геометрии в системе Вейля

2.1 Элементы сферической геометрии

В этом пункте рассмотрены элементы так называемой сферической геометрии - геометрии сферы евклидова пространства. Кратчайшими (геодезическими) или прямыми линиями на сфере являются большие окружности, т. е. такие окружности, плоскости которых проходят через центр данной сферы.

Так как любые два больших круга пересекаются, то в сферической геометрии не осуществляется ни постулат Евклида, ни аксиома параллельности Лобачевского. В этой геометрии не выполняется также ряд других фактов абсолютной геометрии.

Например, прямые в сферической геометрии замкнуты и на них невозможно установить понятие точки, лежащей «между» для трех точек, инцидентных прямой, так как каждую из этих точек на окружности можно считать точкой, лежащей между двумя другими. Две точки на большом круге определяют два отрезка и прямые имеют конечную длину. Таким образом, аксиомы порядка в сферической геометрии должны описывать свойства циклического расположения точек на прямой. И все же, несмотря на указанные различия в сферической геометрии имеется много свойств, аналогичных соответствующим свойствам в евклидовой геометрии и геометрии Лобачевского. Эти геометрии, включая и геометрию достаточно малых кусков сферы, в основных вопросах не противопоставляются между собою, а копируют друг друга.

Возьмем на сфере три точки А, В, С, не лежащие в одной плоскости с центром О данной сферы. Совокупность этих точек и дуг АВ, ВС и АС больших окружностей, меньших полуоборота, называется сферическим треугольником АВС. Точки А, В, С называются вершинами сферического треугольника, а дуги, АВ, ВС, АС — его сторонами. Углом А сферического треугольника АВС называется, угол между касательными, проведенными к дугам АВ и АС в точке их пересечения А. Очевидно, этот угол является линейным углом двугранного угла, образованного плоскостями больших окружностей АВ и АС. Ясно, что сферический треугольник можно получить с помощью трехгранного угла, если пересечь его сферой, центр которой будет совпадать с вершиной данного угла. В самом деле, в пересечении сферы с гранями данного трехгранного угла получим сферический треугольник.

Из школьного курса геометрии известно, что в трехгранном угле любой его плоский угол меньше суммы двух других плоских углов и больше их разности. В геометрии сферы этому предложению соответствует следующая теорема. Во всяком сферическом треугольнике каждая сторона меньше суммы двух других его сторон и больше их разности.

На основании этой теоремы, как и в обычной планиметрии, доказывается, что в сферическом треугольнике против большей стороны лежит больший угол и, обратно, против большего угла лежит большая сторона.

В этой геометрии имеются сферические двуугольники — фигуры более простые, чем сферические треугольники. Сферический двуугольник, по определению, представляет часть сферы, ограниченную двумя большими полуокружностями, пересекающимися в двух диаметрально противоположных точках.

Симметрия сферы относительно диаметральной плоскости и поворот ее вокруг диаметра на данный угол, очевидно, представляют собой примеры преобразований сферы, при которых расстояния между любыми двумя точками равно расстоянию между их образами. Приведем общее определение.

Преобразования сферы, при которых сохраняются расстояния между любыми двумя ее точками, называются движениями. Сферическая геометрия изучает свойства фигур, сохраняющиеся при любых движениях сферы.

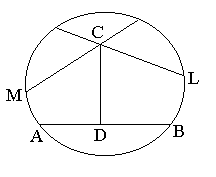
Полярные треугольники

Всякая плоскость , проходящая через центр сферы, пересекает эту сферу по большой окружности. Концы А, А' диаметра, перпендикулярного плоскости , называются полюсами этой окружности. В этом случае большая окружность называется полярой точек А и А'.

Очевидно, все точки поляры удалены от своего полюса на расстояние, равное R/2, где R обозначает радиус данной сферы. Ясно также, что если данная точка удалена от двух точек большой окружности на расстояние R/2, то она является полюсом этой большой окружности. Перейдем теперь к определению полярного треугольника.

Если вершины треугольника АВС являются полюсами сторон другого сферического треугольника А₁В₁С₁, то этот последний называется полярным треугольником по отношению к данному.

Таким образом, радиус-вектор  перпендикулярен векторам  и , т. е.

Аналогично будем иметь

Отсюда следует, что если треугольник А₁В₁С₁ будет полярным к треугольнику АВС, то треугольник АВС в свою очередь будет полярным по отношению к треугольнику А₁В₁С₁.

Таким образом, сферические треугольники АВС и А₁В₁С₁, взаимно полярны друг другу.

Будем обозначать вершины и углы сферического треугольника большими буквами латинского алфавита А, В, С, а противоположные им стороны — соответствующими малыми буквами того же алфавита а, Ь, с. Вершины и противоположные им стороны полярного треугольника будем обозначать теми же буквами с индексами А₁, В₁, С₁, соответственно a₁, b₁, c₁.

Линейные элементы треугольника здесь и в дальнейших формулах входят в виде отношений к радиусу сферы, поэтому целесообразно ввести следующее понятие приведенной длины. Расстояние между двумя точками на сфере, отнесенное к ее радиусу, будем называть приведенным расстоянием.

Докажем следующее предложение о взаимно полярных треугольниках.

Теорема. Угол одного сферического треугольника и соответствующая ему приведенная сторона взаимно полярного треугольника дополняют друг друга до , т. е.

и т. д. Так как

 (*)

То из (*) следует, что

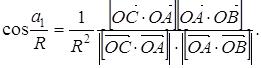
Таким образом, выводим

Аналогично доказываются остальные равенства:

Перейдем к выводу некоторых формул сферической геометрии.

Формулы прямоугольного треугольника в сферической геометрии

Перейдем к выводу некоторых формул сферической геометрии. Пусть в евклидовом пространстве нам дана сфера радиуса R. Возьмем на ней прямоугольный треугольник AВС со сторонами a, b, с, которые будут дугами больших кругов соответственно ВС, СА и АВ, причем условимся считать (рис. 2). Последнее означает, что касательные в точке С, проведенные к большим дугам СА, СВ, перпендикулярны. Выясним связь между линейными и угловыми элементами данного прямоугольного треугольника.

Опустим из точки В перпендикуляры ВС₁, и ВА₁ на прямые ОС и ОА евклидова пространства. Из треугольника ОВС₁, имеем

 (*)

Аналогично из треугольников OBA₁и BA₁C₁ следует, что

(**)

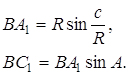Исключая из этих трех соотношений BC₁ и BA₁, получим

 (1.1)

Формула (1.1) показывает, что синус приведенного катета равняется синусу приведенной гипотенузы, умноженному на синус противолежащего угла треугольника.

В предыдущем рассуждении основание С₁, перпендикуляра ВС₁, может совпадать с центром сферы или быть левее его на диаметре ОС. Но можно убедиться, что получаемые ниже формулы, как и формула (1.1), будут всегда справедливы. Кстати отмечу еще раз, что рассматриваются только такие сферические треугольники, которые определяются его вершинами и наименьшими дугами больших окружностей, попарно их соединяющими.

Выясним связь гипотенузы c с катетами а и b. Из треугольника ОВС₁, имеем

(1.2)

Далее из треугольника ОВА₁ и ОС₁А₁ следует, что

Исключая из полученных трех равенств ОС₁ и ОА₁ будем иметь

. (1.3)

Эта формула выражает теорему Пифагора: косинус приведенной гипотенузы прямоугольного треугольника равняется произведению косинусов приведенных катетов. Аналогичным образом выводятся другие формулы. Например, из прямоугольного треугольника А₁ВС₁ следует, что

 (1.4)

Далее, так как

то из (1.2) имеем

(1.5)

С другой стороны,

(1.6)

Из (*, 1.4- 1.6) вытекает, что

(1.7)

Наряду с этой формулой справедлива также парная формула

 (1.7')

Перемножая почленно последние два соотношения, получим

Отбрасывая ненулевые сомножители и применяя теорему Пифагора, окончательно будем иметь

 (1.8)

Возьмем теперь другое выражение А₁С₁ через соs A. Так как

то из (**) и (1.5-1.6), имеем

Отсюда следует, что

(1.9)

Из (1.1) вытекает также, что

Последние два равенства дают

Или

(1.10)

Доказанные формулы прямоугольного треугольника можно выписать, пользуясь так называемым правилом Непера. Чтобы сформулировать это правило, условимся располагать элементы прямоугольного треугольника а, В, с, А, b в указанном на циклическом порядке.

Для каждого из этих элементов предшествующий и последующий элементы называются прилежащими, а остальные два элемента — противолежащими. Для катета b, например, элементы a, А будут прилежащими, а элементы с, В — противолежащими. Прилежащими элементами для гипотенузы являются углы A и В, а противолежащими — катеты а и b.

Сформулируем теперь правило Непера. Косинус любого элемента сферического прямоугольного треугольника равняется произведению синусов противолежащих элементов или произведению котангенсов прилежащих элементов. Если под знаком функции стоит катет, то тригонометрическая функция меняется на смежную - синус а косинус, тангенс на котангенс и наоборот. Заметим также, что во всех формулах длины катетов и гипотенузы делятся на радиус сферы R.

Формулы косоугольного треугольника в сферической геометрии

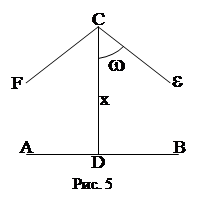
Получим сначала теорему косинусов. Пусть АВС произвольный сферический треугольник. Опустим из вершины В высоту ВD. Применяя к треугольнику ВDС теорему Пифагора, получим

,

где d=AD, a=BC, b=BC, AB=c.

Перепишем предыдущее равенство, преобразуя второй множитель о формуле косинуса разности:

.(1.11)

Первый и третий множители в первом члене правой части по теореме Пифагора дают . Упростим второй член в правой части. Так как

,

то заменяя  по формуле (1.9) на , получим

Таким образом, из (1.11) следует, что

 (1.12)

Эта зависимость, выражающая сторону сферического треугольника через две другие стороны в косинус противолежащего угла, называется теоремой косинусов.

Докажем теперь теорему синусов. Из прямоугольного треугольника АВD и ВDС (рис. 6) получаем

Отсюда следует, что

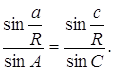
Если опустить теперь высоту из вершины А, то будем иметь

Следовательно

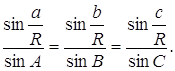 (1.13)

Эти зависимости сторон и синусов противолежащих углов составляют теорему синусов сферического треугольника АВС.

Вторая теорема косинусов

Предположим, что сферический треугольник А₁В₁С₁, является полярным к данному треугольнику АВС. Применяя к нему теорему косинусов, получим

Но в силу формул (см. Полярные треугольники), имеем

Заменяя в предыдущем равенстве стороны и углы только что выписанными выражениями, получим

Или

 (*)

Формула и составляет содержание 2-й теоремы косинусов: Косинус угла сферического треугольника равен произведению косинусов двух других углов, взятому с обратным знаком, и сложенному с произведением синусов тех же углов на косинус приведенной противоположной стороны. Аналогичные две формулы можно получить круговой заменой линейных и угловых элементов данного треугольника АВС.

Из второй теоремы косинусов следует, что в сферической геометрии не существует неравных треугольников с соответственно равными углами. Другими словами, если углы, одного сферического треугольника равны соответствующим углам другого сферического треугольника, то такие треугольники равны.

В заключение установим лишь совпадение формул сферической геометрии для фигур с малыми линейными размерами с соответствующими формулами евклидовой геометрии.

О сферической геометрии в малом

Пусть линейные размеры а, b, с сферического треугольника малы по сравнению с радиусом сферы R. Очевидно, эти условия можно осуществить за счет малости указанных линейных размеров или за счет выбора достаточно большого значения R. Из формулы, выражающей теорему косинусов, следует

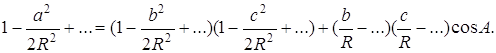
Учитывая в этом равенстве члены до второго порядка малости включительно, получим теорему косинусов евклидовой геометрии:

 (1.14)

В случае прямоугольного сферического треугольника с углом имеем cos A=0 и формула (1.12) в пределе приводит к соотношению

,

составляющему теорему Пифагора в геометрии Евклида. Это равенство следует также из (1.14) при .

Так как при малых размерах приведенных сторон их синусы в первом приближении пропорциональны аргументам, то из (1.13) следуют две связи

,

выражающие теорему синусов в евклидовой геометрии.

Следовательно, формулы сферической геометрии для фигур с малыми линейными размерами по сравнению с радиусом сферы совпадают с соответствующими формулами евклидовой геометрии. Аналогичный результат получим ниже при рассмотрении формул геометрии Лобачевского.