Навигация
2. Гамма-функция
2.1 Определение Восклицательный знак в математических трудах обычно означает взятие факториала какого-либо целого неотрицательного числа:n! = 1·2·3·...·n.
Функцию факториал можно еще записать в виде рекурсионного соотношения:
(n+1)! = (n+1)·n!.
Это соотношение можно рассматривать не только при целых значениях n.
Рассмотрим разностное уравнение
G(z+1)=zG(z).
(2.1)
Несмотря на простую форму записи, в элементарных функциях это уравнение не решается. Его решение называется гамма-функцией. Гамма-функцию можно записать в виде ряда или в виде интеграла. Для изучения глобальных свойств гамма-функции обычно пользуются интегральным представлением.
2.2 Интегральное представление
Перейдем к решению этого уравнения. Будем искать решение в виде интеграла Лапласа:
![]()
В этом случае правая часть уравнения (2.1) может быть записана в виде:
![]()
![]()
Эта формула справедлива, если существуют пределы для внеинтегрального члена. Заранее нам не известно поведение образа [(G)\tilde](p) при p® ±¥. Предположим, что образ гамма-функции таков, что внеинтегральное слагаемое равно нулю. После того, как будет найдено решение, надо будет проверить, верно ли предположение о внеинтегральном слагаемом, иначе придется искать G(z) как-нибудь по-другому.
Левая часть равенства (2.1) записывается следующим образом:
![]()
![]()
Тогда уравнение (2.1) для образа гамма-функции имеет вид:
![]()
Это уравнение легко решить:
![]()
(2.2)
Нетрудно заметить, что найденная функция [(Г)\tilde](p) на самом деле такова, что внеинтегральный член в формуле (2.2) равен нулю.
Зная образ гамма-функции, легко получить и выражение для прообраза:
![]()
Это неканоническая формула, для того, чтобы привести ее к виду, полученному Эйлером, надо сделать замену переменной интегрирования: t = exp(-p), тогда интеграл примет вид:
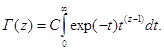
Постоянная C выбирается так, чтобы при целых значениях z гамма-функция совпадала с функцией факториал: Г(n+1) = n!, тогда:

следовательно C = 1. Окончательно, получаем формулу Эйлера для гамма-функции:
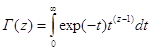
(2.3)
Эта функция очень часто встречается в математических текстах. При работе со специальными функциями, пожалуй, даже чаще, чем восклицательный знак.
Проверить, что функция, определенная формулой (2.3), действительно удовлетворяет уравнению (2.1), можно, проинтегрировав интеграл в правой части этой формулы по частям:
![]()

2.3 Область определения и полюсы
В подынтегральной функции интеграла (2.3) при ![]() экспонента exp(-tz) при R(z) > 0 убывает гораздо быстрее, чем растет алгебраическая функция t(z-1). Особенность в нуле - интегрируемая, поэтому несобственный интеграл в (2.3) сходится абсолютно и равномерно при R (z) > 0. Более того, последовательным дифференцированием по параметру z легко убедиться, что Г(z) - голоморфная функция при R (z) > 0. Однако, непригодность интегрального представления (2.3) при R (z)
экспонента exp(-tz) при R(z) > 0 убывает гораздо быстрее, чем растет алгебраическая функция t(z-1). Особенность в нуле - интегрируемая, поэтому несобственный интеграл в (2.3) сходится абсолютно и равномерно при R (z) > 0. Более того, последовательным дифференцированием по параметру z легко убедиться, что Г(z) - голоморфная функция при R (z) > 0. Однако, непригодность интегрального представления (2.3) при R (z) ![]() 0 не означает, что там не определена сама гамма-функция - решение уравнения (2.1).
0 не означает, что там не определена сама гамма-функция - решение уравнения (2.1).
Рассмотрим поведение Г(z) в окрестности нуля. Для этого представим:
![]()
где ![]() - голоморфная функция в окрестности z = 0. Из формулы (2.1) следует:
- голоморфная функция в окрестности z = 0. Из формулы (2.1) следует:
![]()
Тогда
![]()
то есть Г(z) имеет полюс первого порядка при z = 0.
Также легко получить:
![]()
то есть в окрестности точки ![]() функция Г(z) также имеет полюс первого порядка.
функция Г(z) также имеет полюс первого порядка.
Таким же образом можно получить формулу:
![]()
(2.4)
Из этой формулы следует, что точки z = 0,-1,-2,... - простые полюсы гамма-функции и других полюсов на вещественной оси эта функция не имеет. Нетрудно вычислить вычет в точке z = -n, n = 0,1,2,...:
![]()
Выясним, имеет ли гамма-функция нули. Для этого рассмотрим функцию
![]()
Полюсы этой функции и есть нули функции Г(z).
Разностное уравнение для I(z) легко получить, воспользовавшись выражением для Г(z):
![]()
Выражение для решения этого уравнения в виде интеграла можно получить так же, как было получено интегральное выражение для гамма-функции - через преобразование Лапласа. Ниже приведены вычисления.ни такие же, как и в п.1).ии теграла будут точки ____________________________________________________________________________
![]()
или
![]()
После разделения переменных получим:
![]()
Проинтегрировав получаем:
![]() или
или ![]()
Переход к прообразу Лапласа дает:
![]()
В полученном интеграле сделаем замену переменной интегрирования:
![]() тогда
тогда ![]()
Здесь важно заметить, что подынтегральная функция при нецелых значениях z имеет точку ветвления t = 0. На комплексной плоскости переменной t проведем разрез по отрицательной вещественной полуоси. Интеграл по этой полуоси представим как сумму интеграла по верхнему берегу этого разреза от ![]() до 0 и интеграла от 0 до
до 0 и интеграла от 0 до ![]() по нижнему берегу разреза. Чтобы интеграл не проходил через точку ветвления, устроим вокруг нее петлю.
по нижнему берегу разреза. Чтобы интеграл не проходил через точку ветвления, устроим вокруг нее петлю.
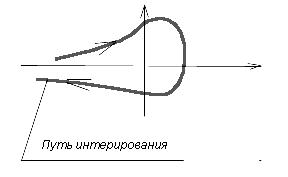
Рис1: Петля в интегральном представлении Ганкеля.
В результате получим:
![]()
Чтобы выяснить значение постоянной, вспомним, что I(1) = 1, с другой стороны:
![]()
Интегральное представление
![]()
(2.5)
называется представлением Ганкеля по петле.
Легко видеть, что функция 1/Г(z) не имеет полюсов в комплексной плоскости, следовательно, гамма-функция не имеет нулей.
С помощью этого интегрального представления можно получить формулу для произведения гамма-функций. Для этого в интеграле сделаем замену переменной ![]() , тогда:
, тогда:
![]()
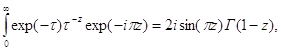
то есть
![]()
Гамма-функцию можно представить в виде бесконечного произведения. Это можно заметить, если в интеграле (2.3) представить
![]()
Тогда интегральное представление гамма-функции:
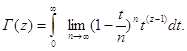
В этой формуле мы можем поменять пределы - предел интегрирования в несобственном интеграле и предел при ![]() внутри интеграла. Приведем результат:
внутри интеграла. Приведем результат:
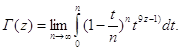
Возьмем по частям этот интеграл:
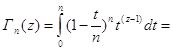
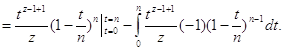
![]()
Если провести эту процедуру n раз, получим:
![]()
Переходя к пределу, получим предельную форму Эйлера для гамма-функции:
![]()
(2.6)
2.6 Формула для произведенияНиже понадобится формула, в которой произведение двух гамма-функций представляется через одну гамма-функцию. Выведем эту формулу, используя интегральное представление гамма-функций.
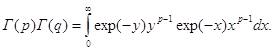
Повторный интеграл представим как двойной несобственный интеграл. Это можно сделать, воспользовавшись теоремой Фубини. В результате получим:
![]()
![]()
Несобственный интеграл равномерно сходится. Его можно рассматривать, например, как интеграл по треугольнику, ограниченному осями координат и прямой x+y = R при R![]() . В двойном интеграле сделаем замену переменных:
. В двойном интеграле сделаем замену переменных:
![]()
![]()
Якобиан этой замены
![]()
Пределы интегрирования: u меняется от 0 до ∞, v при этом меняется от 0 до 1. В результате получим:
![]()
Перепишем опять этот интеграл как повторный, в результате получим:
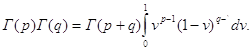
где Rp > 0, Rv > 0.
2. Производная гамма функцииИнтеграл
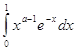
сходится при каждом ![]() ,поскольку
,поскольку ![]() ,и интеграл
,и интеграл ![]()
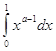 при
при ![]() сходится.
сходится.
В области ![]() , где
, где ![]() - произвольное положительное число, этот интеграл сходится равномерно, так как
- произвольное положительное число, этот интеграл сходится равномерно, так как![]() и можно применить признак Вейрштраса. Сходящимся при всех значениях
и можно применить признак Вейрштраса. Сходящимся при всех значениях ![]() является и весь интеграл
является и весь интеграл 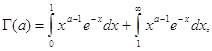 так как и второе слагаемое правой части является интегралом, заведомо сходящимся при любом
так как и второе слагаемое правой части является интегралом, заведомо сходящимся при любом![]() .Легко видеть что интеграл сходится по
.Легко видеть что интеграл сходится по![]() в любой области
в любой области ![]() где
где ![]() произвольно. Действительно для всех указанных значений
произвольно. Действительно для всех указанных значений ![]() и для всех
и для всех ![]()
![]() ,и так как
,и так как 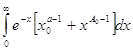 сходится, то выполнены условия признака Вейерштрасса. Таким образом , в области
сходится, то выполнены условия признака Вейерштрасса. Таким образом , в области ![]() интеграл
интеграл 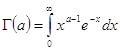 сходится равномерно.
сходится равномерно.![]()
Отсюда вытекает непрерывность гамма функции при![]() .Докажем дифференцируемость этой функции при
.Докажем дифференцируемость этой функции при ![]() .Заметим что функция
.Заметим что функция ![]() непрерывна при
непрерывна при ![]() и
и![]() , и покажем ,что интеграл :
, и покажем ,что интеграл :
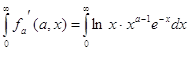
сходится равномерно на каждом сегменте ![]() ,
, ![]() . Выберем число
. Выберем число![]() так , чтобы
так , чтобы ![]() ; тогда
; тогда ![]() при
при ![]() .Поэтому существует число
.Поэтому существует число ![]() такое , что
такое , что ![]() и
и ![]() на
на![]() .Но тогда на
.Но тогда на ![]() справедливо неравенство
справедливо неравенство
![]()
и так как интеграл 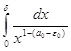 сходится, то интеграл
сходится, то интеграл 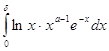 сходится равномерно относительно
сходится равномерно относительно ![]() на
на ![]() . Аналогично для
. Аналогично для ![]() существует такое число
существует такое число ![]() , что для всех
, что для всех ![]() выполняется неравенство
выполняется неравенство 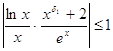 . При таких
. При таких ![]() и всех
и всех ![]() получим
получим ![]() , откуда в силу признака сравнения следует , что интеграл
, откуда в силу признака сравнения следует , что интеграл 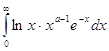 сходится равномерно относительно
сходится равномерно относительно ![]() на
на ![]() . Наконец , интеграл
. Наконец , интеграл
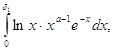
в котором подынтегральная функция непрерывна в области
![]() , очевидно, сходится равномерно относительно
, очевидно, сходится равномерно относительно ![]() на
на ![]() . Таким образом , на
. Таким образом , на ![]() интеграл
интеграл
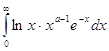
сходится равномерно , а, следовательно , гамма-функция бесконечно дифференцируема при любом ![]() и справедливо равенство
и справедливо равенство
![]()
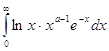 .
.
Относительно интеграла ![]() можно повторить те же рассуждения и заключить, что
можно повторить те же рассуждения и заключить, что
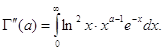
По индукции доказывается , что Г-функция бесконечно дифференцируема при![]() и для ее я
и для ее я ![]() -ой производной справедливо равенство
-ой производной справедливо равенство

Изучим теперь поведение ![]() - функции и построим эскиз ее графика. (см. Приложение 1)
- функции и построим эскиз ее графика. (см. Приложение 1)
Из выражения для второй производной ![]() -функции видно, что
-функции видно, что ![]() для всех
для всех ![]() . Следовательно,
. Следовательно, ![]() возрастает. Поскольку
возрастает. Поскольку ![]() , то по теореме Роля на сегменте [1,2]производная
, то по теореме Роля на сегменте [1,2]производная ![]() при
при ![]() и
и![]() при
при ![]() , т. е. Монотонно убывает на
, т. е. Монотонно убывает на ![]() и монотонно возрастает на
и монотонно возрастает на ![]() . Далее , поскольку
. Далее , поскольку ![]() , то
, то ![]() при
при ![]() . При
. При ![]() из формулы
из формулы ![]() следует , что
следует , что ![]() при
при ![]() .
.
Равенство ![]() , справедливое при
, справедливое при ![]() , можно использовать при распространении
, можно использовать при распространении ![]() - функции на отрицательное значение
- функции на отрицательное значение ![]() .
.
Положим для![]() , что
, что ![]() . Правая часть этого равенства определена для
. Правая часть этого равенства определена для ![]() из (-1,0). Получаем, что так продолженная функция
из (-1,0). Получаем, что так продолженная функция ![]() принимает на (-1,0) отрицательные значения и при
принимает на (-1,0) отрицательные значения и при ![]() , а также при
, а также при ![]() функция
функция ![]() .
.
Определив таким образом ![]() на
на ![]() , мы можем по той же формуле продолжить ее на интервал (-2,-1). На этом интервале продолжением
, мы можем по той же формуле продолжить ее на интервал (-2,-1). На этом интервале продолжением ![]() окажется функция, принимающая положительные значения и такая, что
окажется функция, принимающая положительные значения и такая, что ![]()
![]()
![]() при
при ![]() и
и ![]() . Продолжая этот процесс, определим функцию
. Продолжая этот процесс, определим функцию ![]() , имеющею разрывы в целочисленных точках
, имеющею разрывы в целочисленных точках ![]() (см. Приложение 1.)
(см. Приложение 1.)
Отметим еще раз, что интеграл
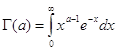
определяет Г-функцию только при положительных значениях ![]() , продолжение на отрицательные значения
, продолжение на отрицательные значения ![]() осуществлено нами формально с помощью формулы приведения
осуществлено нами формально с помощью формулы приведения ![]()
![]() .
.
Похожие работы
... больших монографий. В 40-50-е гг. он участвовал в нескольких научных и философских дискуссиях. С позиции картезинского механического материализма, который сочетался у него с глубокой личной религиозностью, Эйлер выступал против учения о монодах и предустановленной гармонии Г.Лейбница и Х.Вольфа. С Ж.Д.Аламбером он вёл спор о свойствах логарифмов отрицательных и мнимых чисел, с Ж.Д.Аламбером и Д. ...
... -функция непрерывна. Ввиду произвольности s0 ζ(s) непрерывна на всей области определения. Теперь почленным дифференцированием ряда (1), пока формально, найдём производную дзета-функции Римана: (2). Чтобы оправдать этот результат, достаточно удостовериться в том, что ряд (2) равномерно сходится на промежутке и воспользоваться теоремой о ...
... - в группе переменных, «зажатых в кулак», но этот «кулак», как мы уже отмечали, легко разжать, выводя на дисплей найденные значения с «первородной» размерностью массы (kg), длины (m) и времени (sec): пакет MathCAD «разжимает» и сам вектор, м составные размерности, приписывая к числам комбинации основных физических единиц. Но не только этим хороша размерность в задачах. Главное то , что она ...
... сигналов. Результаты изучения связи между фрактонным спектром и фрактальными характеристиками упругих сред могут быть использованы для развития методов исследования геодинамики нефтегазоносных систем, геологоразведки и геофизического мониторинга месторождений нефти и газа. Разрабатываемые в настоящее время на основе современных достижений физики фракталов, геофизики и математическ

0 комментариев