Навигация
Примеры вычисления интегралов
5. Примеры вычисления интегралов
Для вычисления необходимы формулы:
![]()
![]()
Г(![]() )
)![]()
Вычислить интегралы
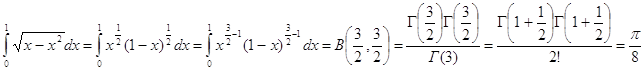
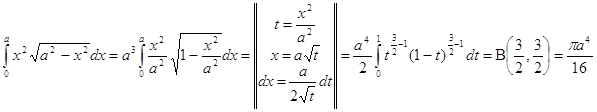
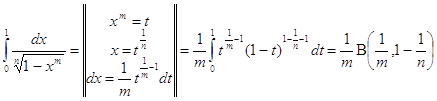
![]()
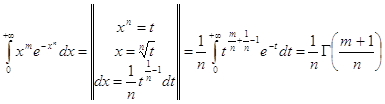
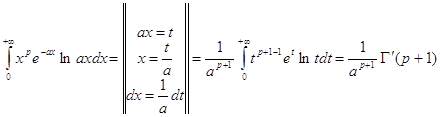
ПРАКТИЧЕСКАЯ ЧАСТЬ
Для вычисления гамма-функции используется аппроксимация её логарифма. Для аппроксимации гамма-функции на интервале x>0 используется следующая формула (для комплексных z):
Г(z+1)=(z+g+0.5)z+0.5exp(-(z+g+0.5))![]() [a0+a1/(z+1)+a2/(z+2)+...+an/(z+n)+eps]
[a0+a1/(z+1)+a2/(z+2)+...+an/(z+n)+eps]
Эта формула похожа на аппроксимацию Стирлинга, но в ней имеется корректирующая серия. Для значений g=5 и n=6, проверено, что величина погрешности ε не превышает 2*10-10. Более того, погрешность не превышает этой величины на всей правой половине комплексной плоскости: z > 0.
Для получения (действительной) гамма-функции на интервале x>0 используется рекуррентная формула Г(z+1)=zГ(z) и вышеприведенная аппроксимация Г(z+1). Кроме того, можно заметить, что удобнее аппроксимировать логарифм гамма-функции, чем ее саму. Во-первых, при этом потребуется вызов только одной математической функции - логарифма, а не двух - экспоненты и степени (последняя все равно использует вызов логарифма), во-вторых, гамма-функция - быстро растущая для больших x, и аппроксимация ее логарифмом снимает вопросы переполнения.
Для аппроксимации Ln(Г(х) - логарифма гамма-функции - получается формула:
log(Г(x))=(x+0.5)log(x+5.5)-(x+5.5)+
log(C0(C1+C2/(x+1)+C3/(x+2)+...+C7/(x+8))/x)
Значения коэффициентов Ck - табличные данные (см. в программе).
Сама гамма-функция получается из ее логарифма взятием экспоненты.
Заключение
Гамма функции являются удобным средством для вычисления некоторых интегралов в частности многих из тех интегралов, которые не представимы в элементарных функциях.
Благодаря этому они широко применяются в математике и ее приложениях, в механике, термодинамике и в других отраслях современной науки.
Список литературы 1. Специальные функции и их приложения: Лебедев И.И.,М.,Гостехтериоиздат,1953
2. Математический анализ часть 2:
Ильин О.А., Садовничий В.А., Сендов Бл.Х.,М.,”Московский университет”,1987
3. Сборник задач по математическому анализу:
Демидович Б.П.,М.,Наука,1966
4. Интегралы и ряды специальные функции:
Прудников А.П., Брычков Ю.А.,М.,Наука,1983
5. Специальные функции:
Кузнецов , М.,”Высшая школа”,1965
6.Асимптотика и специальные функции
Ф.Олвер, М.,Наука,1990.
7.Зоопарк чудовищ или знакомство со спецмальными функциями
О.М.Киселёв,
ПРИЛОЖЕНИЯ
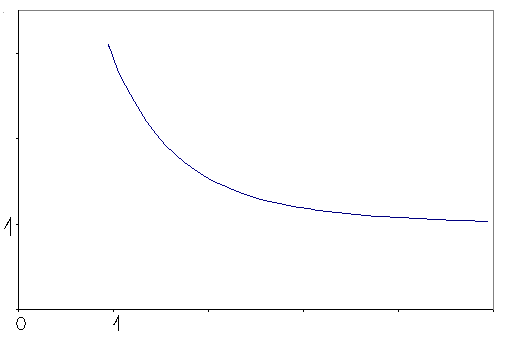
Приложение 1 - График гамма-функции действительного переменного
Приложение 2 – График Гамма-функции
Таблица – таблица значений гамма-функции при некоторых значениях аргумента.
Приложение 3 – листинг программы, рисующий таблицу значений гамма-функции при некоторых значениях аргумента.
Приложение 4 – листинг программы, рисующей график гамма-функции
СОДЕРЖАНИЕ
Реферат............................................................. ...................................3
Введение........................................................... ...................................4
Теоретическая часть…………………………………………………….5
Бета функция Эйлера…………………………………………….5
Гамма функция................................................. ...................................8
2.1. Определение………………………………………………...8
2.2. Интегральное представление………………………………8
2.3. Область определения и полюсы…………………………..10
2.4. Представление Ганкеля через интеграл по петле………..10
2.5. Предельная форма Эйлера………………………………...12
2.6. Формула для произведения………………………………..13
Производная гамма функции ........................ ..................................15
Вычисление интегралов. Формула Стирлинга...........................18
Примеры вычислений интегралов................... ..................................23
Практическая часть…………………………………………………….24
Заключение....................................................... ..................................25
Список литературы……………………………………………..............26
Приложения……………………………………………………………..27
ПРИЛОЖЕНИЕ 1
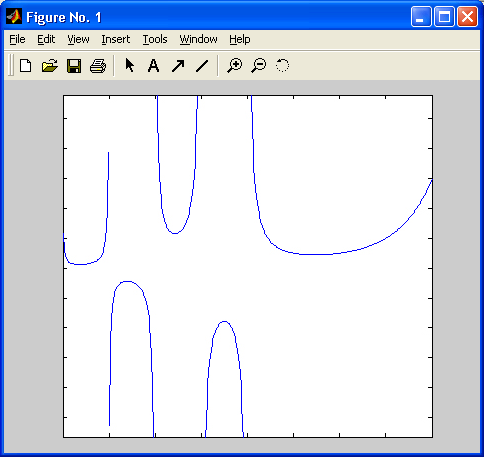
График гамма-функции действительного переменного
ПРИЛОЖЕНИЕ 2
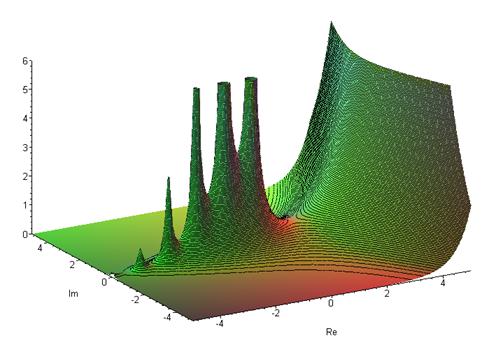
График Гамма-функции
ТАБЛИЦА
| х | g(x) |
| 1.450 1.452 1.454 1.458 1.460 1.462 1.464 1.466 1.468 1.470 1.472 1.474 1.476 1.478 1.480 | 0.8856616058 0.8856432994 0.8856284520 0.8856170571 0.8856091082 0.8856045988 0.8856035228 0.8856058736 0.8856116452 0.8856208314 0.8856334260 0.8856494230 0.8856688165 0.8856916004 0.8857177690 |
ПРИЛОЖЕНИЕ 3
#include<stdio.h>
#include<stdlib.h>
#include<iostream.h>
#include<math.h>
#include<conio.h>
#define CN 8
static double cof[CN]={
2.5066282746310005,
1.0000000000190015,
76.18009172947146,
-86.50532032941677,
24.01409824083091,
-1.231739572450155,
0.1208650973866179e-2,
-0.5395239384953e-5,
};
double GammLn(double x) {
double lg,lg1;
lg1=log(cof[0]*(cof[1]+cof[2]/(x+1)+cof[3]/(x+2)+cof[4]/(x+3)+cof[5]/(x+4)+cof[6]/(x+5)+cof[7]/(x+6))/x);
lg=(x+0.5)*log(x+5.5)-(x+5.5)+lg1;
return lg;
}
double Gamma(double x) {
return(exp(GammLn(x)));
}
void main()
{
double x[8],g[8];
int i,j;
clrscr();
cout<<"vvedite x[1]";
cin>>x[1];
printf("\n\t\t\t_________________________________________");
printf("\n\t\t\t| x |Gamma(x) |");
printf("\n\t\t\t_________________________________________");
for(i=1;i<=8;i++)
{
x[i+1]=x[i]+0.5;
g[i]=Gamma(x[i]);
printf("\n\t\t\t| %f | %f |",x[i],g[i]);
}
printf("\n\t\t\t_________________________________________");
printf("\n Dlia vuhoda iz programmu najmite lybyiy klavishy");
getch();
}
ПРИЛОЖЕНИЕ 4
#include<stdio.h>
#include<graphics.h>
#include<math.h>
#include<conio.h>
Double gam(double x, double eps)
{
Int I, j, n, nb;
Double dze[5]={1.6449340668422643647,
1.20205690315959428540,
1.08232323371113819152,
1.03692775514336992633,
1.01734306198444913971};
Double a=x, y, fc=1.0, s, s1, b;
If(x<=0)
{
Printf (“вы ввели неправильные данные, попробуйте снова\n”); return -1.0;
}
If(x<i)
{
A=x+1.0;
Fc=1.0/x;
}
While (a>=2)
{
A=a-1.0;
Fc=fc*a;
}
A=a-1.0;
If(a==0) return fc;
B=a*a;
S=0;
For (i=0;i<5;i++)
{
S=s+b*dze[i]/(i+2.0);
B=-b*a;
}
Nb=exp((i.0/6.0)*(7.0*log(a)-log(42/0)-log(eps)))+I;
For (n=1;n<=nb;n++)
{
B=a/n;
Si=0;
For(j=0; j<5; j++)
{
Si=si+b/(j+1.0);
B=-b*a/n;
}
S=s+si-log(1.0+a/n);
}
Y=exp(-ce*a+s);
Return y*fc;
}
Main()
}
Double dx,dy, xfrom=0,xto=4, yto=5, h, maxy, miny;
Int n=100, I, gdriver=DETECT, gmode, X0, YN0, X, Y, Y0,pr=0;
Initgraph(&gdriver,&gmode, “ ”);
X0=30;
YN0=getmaxy()-20;
Line(30, getmaxy ()-10,30,30);
Line(20, getmaxy ()-30, getmaxx ()-20, getmaxy ()-30);
X=170;
Y=450;
Do{
Moveto(X,Y);
DO{
Y=Y-1;
Lineto(X,Y);
Y=Y-10;
Moveto(X,Y);
}while (Y>30);
X=X+150;
Y=450;
}while (X<700);
X=30;
Y=366;
Do{
Moveto(X,Y);
Do{
X=X+1;
Lineto(X,Y);
X=X+10;
Moveto(X,Y);
}while (X<=620);
Y=Y-84;
X=30;
}while (y>=30);
X=30+150.0*0,1845;
Moveto(X,30);
For9i=1;i<n,i++)
{
Dx=(4.0*i)/n;
Dy=gam(dx,1e-3);
X=30+(600/0*i)/n;
Y=450-84*dy;
If(Y<30) continue;
Lineto (X,Y);
}
X=30+150.0*308523;
Lineto(X,30);
Line (30,30,30,10);
Line(620,450,640,450);
Line(30,10,25,15);
Line(30,10,25,15);
Line(640,450,635,445);
Line(640,450,635,455);
Line(170,445,170,455);
Line(320,445,320,455);
Line(470,445,470,455);
Line(620,445,620,455);
Line(25,366,35,366);
Line(25,282,35,282);
Line(25,114,35,114);
Line(25,30,35,30);
Outtexty(20,465,"0");
Outtexty(165,465, "1";
Outtexty(315,465, "2";
Outtexty(465,465, "3";
Outtexty(615,465, "4";
Outtexty(630,465, "x";
Outtexty(15,364, "1";
Outtexty(15,280, "2";
Outtexty(15,196, "3";
Outtexty(15,112, "4";
Outtexty(15,30, "5";
Outtexty(15,10, "y";
Getch()
}
Похожие работы
... больших монографий. В 40-50-е гг. он участвовал в нескольких научных и философских дискуссиях. С позиции картезинского механического материализма, который сочетался у него с глубокой личной религиозностью, Эйлер выступал против учения о монодах и предустановленной гармонии Г.Лейбница и Х.Вольфа. С Ж.Д.Аламбером он вёл спор о свойствах логарифмов отрицательных и мнимых чисел, с Ж.Д.Аламбером и Д. ...
... -функция непрерывна. Ввиду произвольности s0 ζ(s) непрерывна на всей области определения. Теперь почленным дифференцированием ряда (1), пока формально, найдём производную дзета-функции Римана: (2). Чтобы оправдать этот результат, достаточно удостовериться в том, что ряд (2) равномерно сходится на промежутке и воспользоваться теоремой о ...
... - в группе переменных, «зажатых в кулак», но этот «кулак», как мы уже отмечали, легко разжать, выводя на дисплей найденные значения с «первородной» размерностью массы (kg), длины (m) и времени (sec): пакет MathCAD «разжимает» и сам вектор, м составные размерности, приписывая к числам комбинации основных физических единиц. Но не только этим хороша размерность в задачах. Главное то , что она ...
... сигналов. Результаты изучения связи между фрактонным спектром и фрактальными характеристиками упругих сред могут быть использованы для развития методов исследования геодинамики нефтегазоносных систем, геологоразведки и геофизического мониторинга месторождений нефти и газа. Разрабатываемые в настоящее время на основе современных достижений физики фракталов, геофизики и математическ

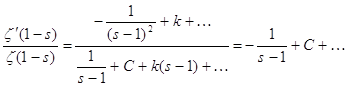
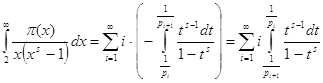
0 комментариев