Навигация
Вычисление некоторых интегралов
20976
знаков
1
таблица
9
изображений
4. Вычисление некоторых интегралов.
Формула Стирлинга
Применим гамма функцию к вычислению интеграла: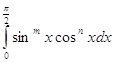
где m > -1,n > -1.Полагая , что 
,имеем
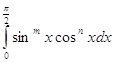
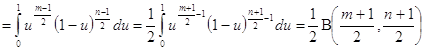
и на основании (2.8) имеем
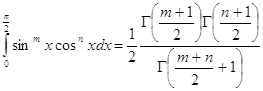
(4.1)
В интеграле
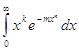
Где k > -1,n > 0,достаточно положить 
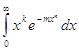
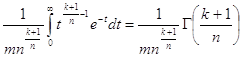
Интеграл
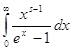
Где s > 0,разложить в ряд
=
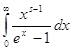
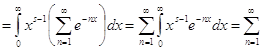
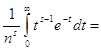
где 
дзетта функция Римана
Рассмотрим неполные гамма функции (функции Прима)
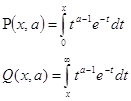
связанные неравенством
Разлагая,
в ряд имеем
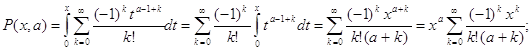
Переходя к выводу формулы Стирлинга , дающей в частности приближенное значение n! при больших значениях n ,рассмотрим предварительно вспомогательную функцию
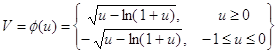(4.2)
Непрерывна на интервале (-1,
) монотонно возрастает от 
до
при изменении 
от 
до и обращаются в 0 при u = 0.Так как
то 
при u > 0 и при u < 0 , далее имеем
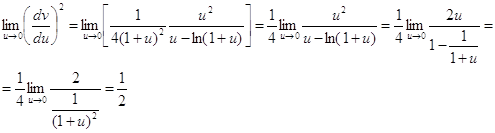
И так производная непрерывна и положительна во всем интервале 
,удовлетворяет условию
Из предыдущего следует, что существует обратная функция, 
определенная на интервале 
непрерывная и монотонно возрастающая в этом интервале,
Обращающаяся в 0 при v=0 и удовлетворяющая условие
(4.3)
Формулу Стирлинга выведем из равенства
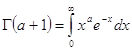
полагая 
,имеем
Положим далее 
введенная выше обратная функция, удовлетворяющая условиям u = -1при 
,и 
при 
.Замечая что(см.4.2)
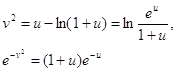
имеем
,
полагая на конец ,
,получим
или
в пределе при 
т.е. при 
(см 4.3)
откуда вытекает формула Стирлинга
которую можно взять в виде
(4.4)
где 
,при
для достаточно больших 
полагают
(4.5)
вычисление же производится при помощи логарифмов
если 
целое положительное число, то 
и (4.5) превращается в приближенную формулу вычисления факториалов при больших значениях n
приведем без вывода более точную формулу
где в скобках стоит не сходящийся ряд.
Похожие работы
... больших монографий. В 40-50-е гг. он участвовал в нескольких научных и философских дискуссиях. С позиции картезинского механического материализма, который сочетался у него с глубокой личной религиозностью, Эйлер выступал против учения о монодах и предустановленной гармонии Г.Лейбница и Х.Вольфа. С Ж.Д.Аламбером он вёл спор о свойствах логарифмов отрицательных и мнимых чисел, с Ж.Д.Аламбером и Д. ...
... -функция непрерывна. Ввиду произвольности s0 ζ(s) непрерывна на всей области определения. Теперь почленным дифференцированием ряда (1), пока формально, найдём производную дзета-функции Римана: (2). Чтобы оправдать этот результат, достаточно удостовериться в том, что ряд (2) равномерно сходится на промежутке и воспользоваться теоремой о ...
... - в группе переменных, «зажатых в кулак», но этот «кулак», как мы уже отмечали, легко разжать, выводя на дисплей найденные значения с «первородной» размерностью массы (kg), длины (m) и времени (sec): пакет MathCAD «разжимает» и сам вектор, м составные размерности, приписывая к числам комбинации основных физических единиц. Но не только этим хороша размерность в задачах. Главное то , что она ...
... сигналов. Результаты изучения связи между фрактонным спектром и фрактальными характеристиками упругих сред могут быть использованы для развития методов исследования геодинамики нефтегазоносных систем, геологоразведки и геофизического мониторинга месторождений нефти и газа. Разрабатываемые в настоящее время на основе современных достижений физики фракталов, геофизики и математическ
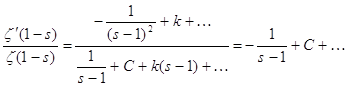
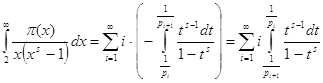
0 комментариев