Навигация
Рассчитать индивидуальные индексы цен и физического объема. Рассчитать общий индекс цен в агрегатной форме по методу Паше, Ласпейреса
31989
знаков
20
таблиц
9
изображений
1. Рассчитать индивидуальные индексы цен и физического объема. Рассчитать общий индекс цен в агрегатной форме по методу Паше, Ласпейреса.
Модель расчета общих индексов методом агрегатного индекса
| Вид продукции | 2003 г | 2004 г | Стоимость продукции | |||||
| В текущих ценах | Текущего периода в сопоставимых ценах | Базового периода в текущих ценах | ||||||
| Цена, руб. | Физический объем, тыс. ед. | Цена, руб. | Физический объем, тыс. ед. | 2003 | 2004 | |||
| Символ | p0 | q0 | p1 | q1 | p0q0 | p1q1 | p 0q1 | p 1q0 |
| А | 8,4 | 1310 | 10,5 | 1215 | 11004 | 12757,5 | 13755 | 10206 |
| Б | 15,5 | 800 | 17,6 | 833 | 12400 | 14660,8 | 14080 | 12911,5 |
| В | 103 | 250 | 106,0 | 207 | 25750 | 21942 | 26500 | 57015 |
| Г | 31,5 | 1845 | 35,9 | 1810 | 58117,5 | 64979 | 66235,5 | 70875 |
| Итого | 158,4 | 2360 | 134,1 | 2250 | 107271,5 | 114339,3 | 120570,5 | 151007,5 |
2. Рассчитать общий индекс физического объема в агрегатной форме.
1.1. Агрегатный индекс физического объема
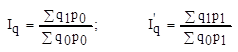
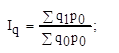= 120570,5/107271,5 = 1.12
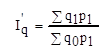= 114339,3/151007,5 = 0.75
3. Рассчитать общий индекс стоимости. Показать взаимосвязь индексов цены, физического объема и стоимости.
Общий индекс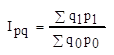 
= 114339,3/107271,5 = 1.065
Система индексов имеет вид:
114339,3 2360 114339,3 120570,5 2250
107271,5 2360 120570,5 107271,5 2250
1,065 = 0,948*1,12
Если бы произошедшие изменения цен не сопровождались структурным перераспределением продаж, то средняя цена товара выросла бы в 0,948 раз, а только изменение структуры продаж вызвало бы рост средней цены на 12%. Одновременное воздействие двух факторов увеличило среднюю цену продаж на 6,5%.
| Вид продукции | 2003 г | 2004 г | ip | iq | ip p0 | iq*q0 | ||
| Цена, руб. | Физический объем, тыс. ед. | Цена, руб. | Физический объем, тыс. ед. | |||||
| Символ | p0 | q0 | p1 | q1 | ||||
| А | 8,4 | 1310 | 10,5 | 1215 | 1,25 | 0.93 | 9,45 | 1218.3 |
| Б | 15,5 | 800 | 17,6 | 833 | 1,135 | 1.041 | 17,59 | 832.8 |
| В | 103 | 250 | 106,0 | 207 | 1,03 | 0.828 | 106,09 | 207 |
| Г | 31,5 | 1845 | 35,9 | 1810 | 1,139 | 0.98 | 35,88 | 1808.1 |
| Итого | 158,4 | 2360 | 134,1 | 2250 | 4.55 | 3.78 | 169,01 | 4066.2 |
Похожие работы
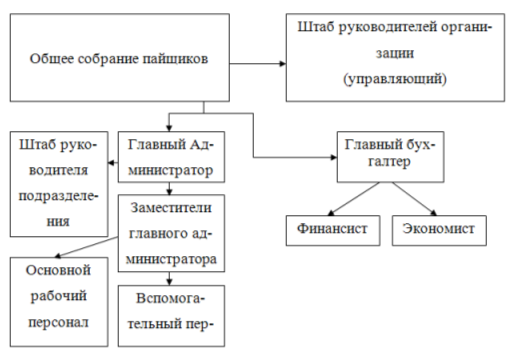
... или = Средний темп роста = Средний темп прироста - 1) или - 100 Средняя величина абсолютного значения на 1 единицу % прироста = Глава II. Статистический анализ по рядам динамики на примере предприятия «Салон красоты Goddess 2.1 История деятельности и структура предприятия «Салон красоты Goddess» «Салон красоты Goddess» осуществляет свою деятельность в ...
... , взаимозависимостью состояний отдельных единиц и наличием вариации. Изменение социально-экономических явлений во времени изучается статистикой методом построения и анализа динамических рядов. Ряды динамики - это значения статистических показателей, которые представлены в определенной хронологической последовательности. Каждый динамический ряд содержит две составляющие: 1) показатели периодов ...
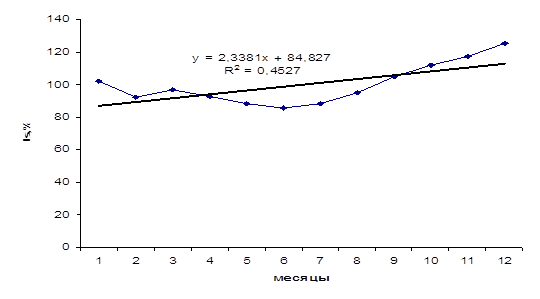
... сезонного характера производства или обращения служит среднее квадратическое отклонение индексов сезонности, то есть: . Сравнение показателей , вычисленных за разные периоды, показывает сдвиги в сезонности. 2. Методы анализа основной тенденции (тренда) в рядах динамики. Одна из важнейших задач статистики- определение в рядах динамики общей тенденции развития. Основной тенденцией развития ...
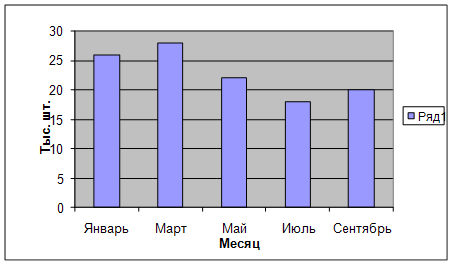
... показатели времени, а по оси ординат – уровни ряда (либо базисные темпы роста). Рис. 1.1. Выпуск продукции по месяцам 1.2 Система статистических показателей, характеризующих аналитические показатели рядов динамики Аналитические показатели рядов динамики строятся на основе сравнения (сопоставления) двух уровней ряда. В каждом ряде динамики, представленном не двумя, а большим числом ...
0 комментариев