Статистика

Содержание

Задача 1 Задача 2 Задача 3 Задача 4 Задача 5 Задача 6 Задача 7 Задача 8 Задача 9 Список литературы
Задача 1

 

Сформируйте массив случайных чисел и произведите 30-процентную простую случайную выборку.

По выборочным данным:

1.         Постройте интервальный ряд распределения, образовав пять групп с равными интервалами.

2.         Исчислите средний объем выпуска товаров и услуг, приходящийся на одно предприятие, а также долю предприятий с объемом выпуска товаров и услуг, более 40 млн. руб.

3.         С вероятностью 0,954 определите доверительные интервалы, в которых можно ожидать генеральные параметры : а)средний размер выпуска товаров и услуг одного предприятия; б) долю малых предприятий с объемом выпуска товаров и услуг малыми предприятиями; г) число предприятий с объемом выпуска товаров и услуг более 40 млн. руб.

Подтвердите достоверность полученных оценок расчетом генеральных характеристик. Сделайте выводы.

Решение:

Выберем 30 случайных двузначных чисел:

77, 26, 33, 72, 95, 29, 03, 04, 19, 14, 22, 57, 08, 17, 69, 65 , 68, 70, 02, 30, 23, 58, 52, 85, 73, 93, 34, 98, 62, 45,

В соответствии с этими числами осуществим 30%-ную выборку.

Сл. число (№ предприятия)	Выпуск товаров и услуг, млн. руб.
77	6
26	30
33	3
72	5
95	7
29	19
3	5
4	3
19	24
14	11
22	41
57	25
08	10
17	5
69	5
65	8
68	4
70	10
2	7
30	17
23	35
58	55
52	35
85	34
73	39
93	8
34	2
98	8
62	20
45	40
Сумма	521 713

Величина интервала

h = (x_max – x_min) / m = (55 – 2) / 5 = 10,6

Границы интервалов:

2 + 10,6 = 12,6

12,6 + 10,6 = 23,2

23,2 + 10,6 = 33,8

33,8 +10,6 = 44,4

44,4 + 10,6 = 55

Интервальный ряд распределения:

Интервал	Частота ni
(2; 12,6)	17
(12,6;23,2)	3
(23,2; 33,8)	3
(33,8; 44,4)	6
(44,4;55)	1

Средний объем товаров и услуг

= ∑ x_i / n = 521 / 30 = 17,4 млн. руб.

Число предприятий с объемом товаров и услуг более 40 млн. руб. равно n₀=2.

Доля предприятий с объемом товаров и услуг более 40 млн. руб.

n₀ / n = 2 / 30 = 0,06

Расчетная таблица:

xi	Xi -	(Xi - )2
6	-11,4	129,2
30	12,6	159,6
3	-14,4	206,4
5	-12,4	152,9
7	-10,4	107,5
19	1,6	2,7
5	-12,4	152,9
3	-14,4	206,4
24	6,6	44,0
11	-6,4	40,5
41	23,6	558,5
25	7,6	58,3
10	-7,4	54,3
5	-12,4	152,9
5	-12,4	152,9
8	-9,4	87,7
4	-13,4	178,7
10	-7,4	54,3
7	-10,4	107,5
17	-0,4	0,1
35	17,6	310,9
55	37,6	1416,3
35	17,6	310,9
34	16,6	276,7
39	21,6	468,0
8	-9,4	87,7
2	-15,4	236,1
8	-9,4	87,7
20	2,6	6,9
40	22,6	512,3
521		6321,0

Среднее квадратическое отклонение

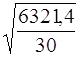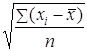σ = =  = 14,5 млн. руб.

Предельная ошибка выборочного среднего (при вероятности 0,954 – t = 2):

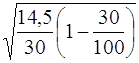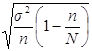Δ = t = 2 * = 1,2

Доверительный интервал для среднего объема товаров и услуг

 - Δ < a < + Δ

17,4 –1,2 < a < 17,4 + 1,2

16,2 < a < 18,6

Предельная ошибка выборочной доли

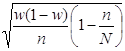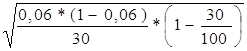Δ = t = 2 *  = 0,07

Доверительный интервал для выборочной доли

0,06 – 0,07 < w < 0,06 + 0,07