Средняя численность внешних совместителей

1.         Средняя численность внешних совместителей

ВС = (70 * 7 / 31) + (85*3/31) = 15,8 + 8,23 = 24,03,

где 70 и 85 – их ежедневная численность, 7 и 3 – число дней работы, 31 – число дней в октябре.

Средняя численность работников, выполнявших работу по договорам гражданско-правового характера

ГП = (15 * 3 / 31) + (10 * 3 / 31) = 1,45 + 0,97 = 2,42,

где 15 и 10 – их ежедневная численность, 3 – число дней работы, 31 – число дней в октябре.

2.         Среднесписочная численность за октябрь

СЧ₁₀ = (315 + 305 + 317 + 320 + 335 + 335 + 334 + 330 + 325 + 310 + 307) / 31 = 114 чел.

Численность работников в выходные дни принимается равной их численности в последний рабочий день недели.

Среднесписочная численность за ноябрь

СЧ₁₁ = (5859 + 3891) / 30 = 325 чел.

Среднесписочная численность за декабрь

СЧ₁₂ = 320 чел.,

Среднесписочная численность за год

СЧ = (31 * СЧ₁₀ + 30 * СЧ₁₁ + 31 * СЧ₁₂) / 365 = (31 * 114 + 30 * 325 + 31 * 320) / 365 = 63,6 чел.,

где 31, 30, 31 – число дней в октябре, ноябре и декабре, 365 – число дней в году.

Выводы: основная часть персона – постоянные работники, первые месяцы численность персонала изменилась почти в 3 раза, затем сократилась на 5 человек.

Задача 8

По субъекту Федерации имеются следующие данные, млрд. руб.:

Основные фонды по полной стоимости на начало года 300

Степень износа основных фондов на начало года, %30

Введено новых основных фондов за год50

Выбыло основных фондов по полной стоимости30

Остаточная стоимость выбывших основных фондов, %45

Сумма начисленного износа за год25

Затраты на капитальный ремонт за год18

Определите:

1)         полную восстановительную стоимость на конец года;

2)         восстановительную стоимость за вычетом износа на начало и конец года;

3)         коэффициенты годности основных фондов на начало и конец года;

4)         коэффициент износа основных фондов на конец года;

5)         коэффициенты обновления и выбытия основных фондов.

6)         Постройте балансы основных фондов по полной восстановительной стоимости за вычетом износа. Сделайте выводы.

Решение

Полная восстановительная стоимость на конец года = 581 + 50 = 631 млн. руб.

Восстановительная стоимость основных фондов с учетом износа на начало года

ВС₀ = ОФ₀ * (1 – И / 100) = 830 * (1 – 30 / 100) = 581 млн. руб.,

где ОФ – полная восстановительная стоимость основных фондов, И – износ.

Полная восстановительная стоимость на конец года

ОФ₁ = 830 – 24 – 35 + 60 + 120 = 951 млн. руб.

Восстановительная стоимость с учетом износа на конец года

ВС₁ = 581 – 24 * 75 / 100 – 35 * 92 / 100 + 52 + 120 = 702,8 млн. руб.

Коэффициент обновления основных фондов

К_о = ОФ_вв / ОФ₁ = (60 + 120) / 951 = 0,189,

где ОФ_вв – стоимость введенных основных фондов.

Коэффициент выбытия

К_в = ОФ_выб / ОФ₀ = (24 + 35) / 830 = 0,071,

где ОФ_выб – стоимость выбывших основных фондов.

Среднегодовая стоимость основных фондов

ОФ = (830 * 2 + 890 * 1 + 866 * 2 + 986 * 3 + 951 * 4) / 12 = 920,3 млн. руб.

Фондовооруженность

ФВ = ОФ / ЧР = 920,3 / 900 = 1,023,

где ЧР – среднегодовая численность рабочих.

Фондоотдача

ФО = В / ОФ = 6 / 920,3 = 0,00652,

где В – выпуск товаров и услуг.

Выводы. Восстановительная стоимость основных фондов (как полная, так и с учетом износа) в течение года увеличилась. Основные фонды обновились на 18,9%. Выбыло 7,1% основных фондов. Фондовооруженность составила 1,023, фондоотдача – 0,00652.

  Задача 9

За отчетный период имеются данные о распределении домохозяйств региона по размеру среднедушевых денежных доходов:

Среднедушевой денежный доход, руб.	Число домохозяйств, %	Численность населения, %
До 800	6,5	7,5
800-1200	29,3	23,4
1200-1600	21,6	21,7
1600-2000	11,4	13,5
2000-2400	9,1	8,4
2400-2800	8,3	7,3
2800-3200	7,0	6,7
3200-3600	3,1	2,5
3600 и более	3,7	9,0
Итого	100,00	100,0

Справочно: Общее число домохозяйств в регионе составляет 806,5 тыс. Одно домохозяйство в среднем состоит из 3,2 лица.

Определите:

1)        среднедушевой месячный доход населения региона;

2)        модальные и медианные размеры среднедушевых месячных доходов населения региона;

3)        показатели дифференциации и концентрации доходов населения региона: а) децильный коэффициент; б) коэффициент К. Джинни; в) коэффициент Херфиндаля-Хиршмана.

4)        численность населения региона, имеющего доход ниже прожиточного минимума, установленного в отчетном периоде в размере 1530 руб.

5)        уровень бедности в регионе. Постройте кривую М. Лоренса.

6)        Сделайте выводы об уровне доходов населения региона и их концентрации.

Решение:

Найдем середины интервалов денежных доходов:

800 – (1200 – 800) / 2 = 600 руб.

(800 + 1200) / 2 = 1000 руб. и т.д.

3600 + (3600-3200)/2 = 3800

Интервалы	Середины интервалов xi	Численность населения mi	Число домохозяйств ni	ximi	xini	Доля насел.	Доля домохозяйств	Доля доходов населения	Доля доходов домохозяйств
До 800	600	194	52,4	116160	31440	0,08	0,06	0,025	0,023
800 – 1200	1000	604	236,3	603900	236300	0,23	0,29	0,128	0,171
1200 – 1600	1400	560	174,2	784000	243880	0,22	0,22	0,166	0,177
1600 – 2000	1800	348	91,9	627120	165420	0,13	0,11	0,133	0,120
2000 – 2400	2200	217	73,4	476960	161480	0,08	0,09	0,101	0,117
2400 – 2800	2600	188	66,9	489840	173940	0,07	0,08	0,104	0,126
2800 - 3200	3000	173	56,5	518700	169500	0,07	0,07	0,110	0,123
3200 – 3600	3400	65	25,0	219300	85000	0,02	0,03	0,046	0,062
3600 и более	3800	232	29,8	882740	113240	0,09	0,04	0,187	0,082
Итого	-	2581	806,5	4718720	1380200

1)        Среднедушевой денежный доход населения региона:

 = ∑ x_im_i/ ∑m_i = 4718734,7 / 2581 = 1828,4 руб.

2)      Модальный интервал для численности населения (800; 1200), так как

max (194; 604; 560; 348; 217; 188; 173; 65; 232) = 604

Мода

Мо₀ = x_o + h (n_mo – n_{mo – 1}) / (2n_mo – n_{mo – 1} – n_{mo + 1}) = 800 + 400 * (604 – 194) / (2 * 604 – 194 – 560) = 1161,2 руб.,

где h = 1200 – 800 = 400 – длина модального интервала, n_mo, n_{mo – 1}, n_{mo + 1} – частоты модального, предмодального и послемодального интервалов.

Номер медианы для численности населения

(N + 1) / 2 = (2581 + 1) / 2 = 1291

Медианный интервал (1200; 1600), так как

194 + 604 = 798 < 1291

194 + 604 + 560 = 1358 > 1291

Медиана

Ме₀ = x_e + h ((N + 1) / 2 – S_{me – 1}) / n_me = 1200 + 400 * (1297 – 798) / 560 = 1556,4 руб.,

где x_e – начало медианного интервала, S_{me – 1} – накопленная частота предмедианных интервалов, n_me – частота медианного интервала.

1) А) Децильный коэффициент

194 < 2581 * 0,1 = 258,1

194 + 604 =798 > 258,1

Нижний децильный интервал (800, 1200).

Нижняя дециль

Д_н = 800 + 400 * (258,1 – 194) / 604 = 842,5 руб.

2581 – 232 = 2349 > 2581 * 0,9 = 2323

2581 – 232 – 65 = 2284 < 2323

Верхний децильный интервал (3200, 3600)

Верхняя дециль

Д_в = 3600 – 400 * (2349 – 2323) / 65 = 3760 руб.

Децильный коэффициент

К_д0 = Д_в / Д_н = 3760 / 842,5 = 4,463

Б) Коэффициент Джини:

G = ,

где cum у_i — кумулятивная доля дохода.

Интервалы	Доля насел. xi	Доля доходов yi	Кумул. доля доходов cum yi
До 800	0,08	0,025	0,025
800 – 1200	0,23	0,128	0,153
1200 – 1600	0,22	0,166	0,319
1600 – 2000	0,13	0,133	0,452
2000 – 2400	0,08	0,101	0,553
2400 – 2800	0,07	0,104	0,657
2800 - 3200	0,07	0,110	0,766
3200 – 3600	0,02	0,046	0,813
3600 - 4000	0,09	0,187	1,000

Население:

G₀ = 1 – 2 * (0,08 * 0,025 + 0,23 * 0,153 + 0,22 * 0,319 + 0,13 * 0,452 + 0,08 * 0,553 + 0,07 * 0,657 + 0,07 * 0,766 + 0,02 * 0,813 + 0,09 * 1,000) + 0,08 * 0,025 + 0,23 * 0,128 + 0,22 * 0,166 + 0,13 * 0,133 + 0,08 * 0,101 + 0,07 * 0,104 + 0,07 * 0,110 + 0,02 * 0,046 + 0,09 * 0,187 = 0,280

в) коэффициент Херфиндаля-Хиршмана

К=0,08*0,08+0,23*0,23+0,22*0,22+0,13*0,13+0,08*0,08 +0,07*0,07+0,07*0,07+0,02*0,02+0,09*0,09 = 1

2)        Численность населения, имеющего доход ниже прожиточного минимума (1530 руб):

Б₀ = 194 + 604 + 560 * (1530 – 1200) / 400 = 1260 тыс. чел.

3)        Уровень бедности

УБ = Б / ЧН * 100

УБ₀ = 1260 / 2581 * 100 = 48,8%

Кривая Лоренца:

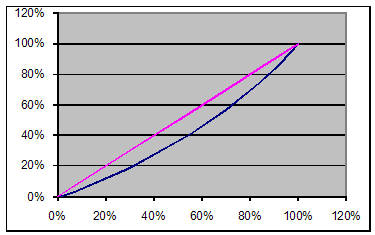
Выводы. Децильный коэффициент увеличился. Коэффициент Джини увеличился, т.е. дифференциация населения по уровню доходов возросла. Уровень бедности увеличился в 2 раза.

Список литературы

1)    Громыко Г.Л. Статистика. – М.: МГУ, 2001.

2)    Гусарев В.М. Теория статистики. – М.: ЮНИТИ, 2002.

3)    Елисеева И.И., Юзбашев М.М. Общая теория статистики / Под ред. чл.-корр. РАН И.И. Елисеевой. - М., 1998.

4)    Ефимова М.Р. и др. Общая теория статистики: Учебник. – М.: ИНФРА-М, 2003.

5)    Ефимова М.Р., Киперман Г.Я. Сборник задач по теории статистики. – М.: Финансы и статистика, 2002.

6)    Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики. М, 2000.

7)    Экономическая статистика: Учебник / Под ред. Е.Н. Фреймундт, М.Р. Эйдельмана. – М.: Статистика, 2003.