Наибольшие затруднения учащиеся испытывают при составлении схемы к задаче (“одевание” схемы) и составлении выражения

2. Наибольшие затруднения учащиеся испытывают при составлении схемы к задаче (“одевание” схемы) и составлении выражения.

3.2. Обучающий эксперимент

Цель эксперимента: продолжить работу по решению задач с использованием деятельностного метода с учениками из гимназии № 5, обучающихся по программе “Школа 2100”. Для формирования более прочных знаний, умений и навыков при решении задач особое внимание было уделено составлению схемы (“одевание” схемы) и составлению выражения по схеме.

Предлагались следующие задания.

1. Игра “Часть или целое?”

c

b

Учитель в быстром темпе движением указки показывает часть или целое на отрезке, учащиеся называют. С целью активации деятельности учащихся следует использовать средства обратной связи. С учетом того, что на письме условились часть и целое обозначать специальными знаками, учащиеся вместо ответа “целое” изображают “кружок”, соединяя большой и указательный пальцы правой руки, а “часть” — располагая указательный палец правой руки горизонтально. Игра позволяет за одну минуту выполнить до 15 заданий с указанной целью.

В другом варианте предложенной игры ситуация более приближена к той, в которой ученики окажутся при моделировании задачи. На доске заранее строятся схемы. Учитель спрашивает, что известно в каждом случае: часть или целое? Отвечая. Учащиеся могут использовать отмеченный выше прием или давать ответ в письменном виде, используя при этом условные обозначения:

¡ — целое

¾ — целое

Могут быть использованы прием взаимопроверки и прием сверки с правильным выполнением на доске заданием.

2. Игра “Что изменилось?”

Перед учащимися схема:

Выясняется, что известно: часть или целое. Затем ученики закрывают глаза, схема принимает вид 2), ученики отвечают на тот же самый вопрос, вновь закрывают глаза, схема преобразовывается и т.д. — столько раз, сколько считает нужным учитель.

Аналогичные задания в игровой форме могут быть предложены учащимся со знаком вопроса. Только задание уже будет формулироваться несколько иначе: “Что неизвестно: часть или целое?”

В предыдущих заданиях учащиеся “читали” схему; не менее важно уметь “одевать”схему.

3. Игра “Одень схему”

До начала урока каждый ученик получает небольшой листочек со схемами, которые “одеваются” по заданию учителя. Задания могут быть такими:

-   а – часть;

-   b – целое;

-   неизвестное целое;

-   неизвестная часть.

4. Игра “Выбери схему”

Учитель читает задачу, а ученики должны назвать номер схемы, на которой знак вопроса поставили в соответствии с текстом задачи. Например: в группе “а” мальчиков и “в” девочек, сколько детей в группе?

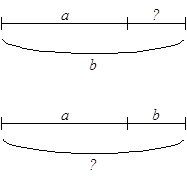
Обоснование ответа может быть следующим. Все дети группы (целое) состоят из мальчиков (часть) и девочек (другая часть). Значит, верно знак вопроса поставлен во второй схеме.

Моделируя текст задачи, ученик должен четко представлять себе, что надо найти в задаче: часть или целое. С этой целью может быть проведена следующая работа.

5. Игра “Что неизвестно?”

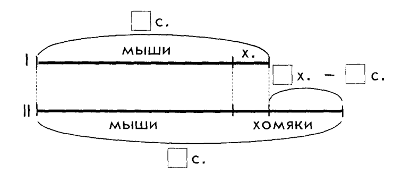
Учитель читает текст задачи, а учащиеся дают ответ на вопрос о том, что неизвестно в задаче: часть или целое. В качестве средства обратной связи может быть использована карточка, имеющая вид:

с одной стороны , с другой: .

Например: в одном пучке 3 морковки, а в другом 5 морковок. Сколько морковок в двух пучках? (неизвестно целое).

Работа может выполняться в форме математического диктанта.

На следующем этапе наряду с вопросом о том, что надо найти в задаче: часть или целое, задается вопрос о том, как это сделать (каким действием). Ученики подготовлены к обоснованному выбору арифметического действия на основе связи между целым и его частями.

Задания:

§  Покажи целое, покажи части. Что известно, что неизвестно?

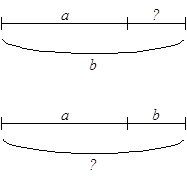
§  Я показываю — вы называете, что это: целое или часть, известно оно или нет?

§  Что больше часть или целое?

§  Как найти целое?

§  Как найти часть?

§  Что можно найти, зная целое и часть? Как? (Каким действием?).

§  Что можно найти, зная части целого? Как? (Каким действием?).

§  Что и что нужно знать, чтобы найти целое? Как? (Каким действием?).

§  Что и что нужно знать, чтобы найти часть? Как? (Каким действием?).

§  Составьте выражение к каждой схеме?

Опорные схемы, используемые на данном этапе работы над задачей, могут иметь следующий вид:

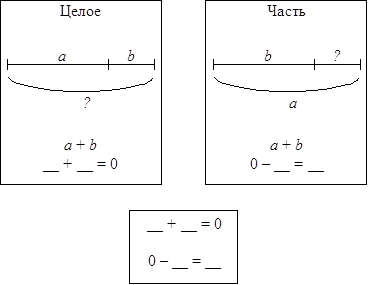
Во время эксперимента ученики придумывали свои задачи, иллюстрировали их, “одевали” схемы, использовалось комментирование, самостоятельная работа с различными видами проверки.

3.3. Контрольный эксперимент

Цель: проверить эффективность подхода при решении простых задач, предложенного образовательной программой “Школа 2100”.

Были предложены задачи:

§     На одной полке стояло 3 книги, а на другой – 4 книги. Сколько книг стояло на двух полках?

§     Во дворе играли 9 детей, из них 5 мальчиков. Сколько было девочек?

§     На березе сидели 6 птиц. Несколько птиц улетело, осталось 4 птицы. Сколько птиц улетело?

§     У Тани было 3 красных карандаша, 2 синих и 4 зеленых. Сколько карандашей было у Тани?

§     Дима за три дня прочитал 8 страниц. В первый день он прочитал 2 страницы, во второй – 4 страницы. Сколько страниц прочитал Дима в третий день?

Вывод. Результат контрольного эксперимента отражен в графике.

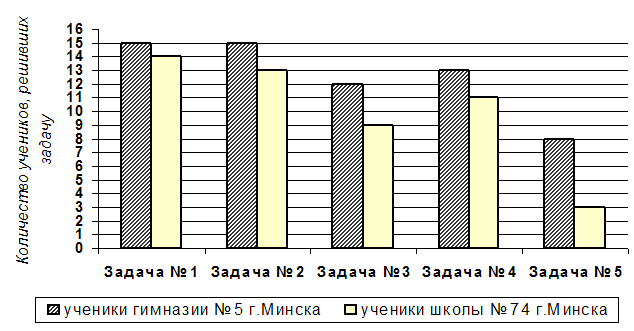
Решили: 63 задачи – ученики гимназии № 5