Навигация
Постановка учебной задачи
2.2. Постановка учебной задачи.
Каждая команда получает по 4 задачи “Блиц-турнира”, табличку и схему.
“Блиц-турнир”а) Одна зайчиха нацепила а колец, а другая — на 2 кольца больше, чем первая. Сколько колец у обеих?
б) У мамы-зайчихи было а колец. Она дала трем дочкам по b колец. Сколько колец у нее осталось?
в) Было а колец красных, b колец белых и с колец розовых. Их раздали 4 зайчихам поровну. По скольку колец получила каждая зайчиха?
г) У мамы-зайчихи было а колец. Она раздала их двум дочкам так, что у одной из них получилось на n колец больше, чем у другой. По скольку колец получила каждая дочка?
![]()
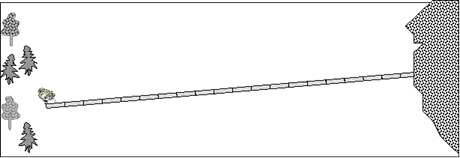
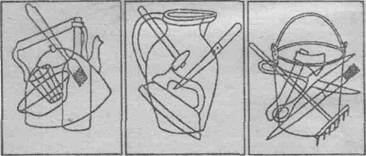
У I команды:
![]()
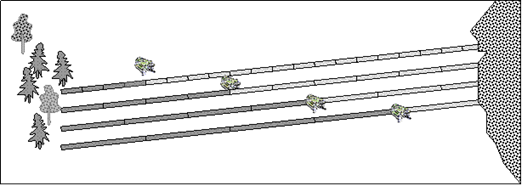
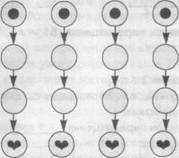
У II команды:
![]()
У III команды:
— Среди зайчих стало модно носить в ушах кольца. Прочитайте задачи на своих листочках и определите, к какой задаче подходит ваша схема и ваше выражение?
Учащиеся обсуждают задачи в группах, совместно находят ответ. По одному человеку от группы “защищает”мнение команды.
— К какой задаче я не подобрала схему и выражение?
— Какая из данных схем подойдет к четвертой задаче?

— Составьте выражение к этой задаче. (Дети предлагают различные варианты решения, одно из них — а: 2.)
— Верно ли это решение? Почему нет? При каком условии мы могли бы считать его правильным? (Если бы количество колец у обеих зайчих было равным.)
— Мы встретились с новым типом задач: в них известна сумма и разность чисел, а сами числа — неизвестны. Наша задача сегодня -научиться решать задачи по сумме и разности.
3. “Открытие” нового знания.
Рассуждения детей обязательно сопровождаются предметными действиями детей с полосками.
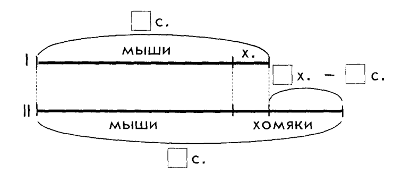
— Положите перед собой полоски цветной бумаги, как это показано на схеме:
![]()
Объясните, какой буквой обозначена на схеме сумма колец? (Буквой а.) Разность колец? (Буквой n.)
— Нельзя ли уравнять количество колец у обеих зайчих? Как это сделать? (Дети отгибают или отрывают часть длинной полоски так, чтобы оба отрезка стали равными.)
— Как записать выражением, сколько стало колец? (а-n)
— Это удвоенное меньшее или большее число? (Меньшее.)
— Как же найти меньшее число? ((а-n): 2.)
— Мы ответили на вопрос задачи? (Нет.)
— Что еще должны узнать? (Большее число.)
— Как найти большее число? (Добавить разницу: (а-n): 2 + n)
Таблички с полученными выражениями фиксируются на доске:
(а-n): 2 — меньшее число,
(а-n): 2 + n — большее число.
— Мы сначала нашли удвоенное меньшее число. А как иначе можно было рассуждать? (Найти удвоенное большее число.)
— Как это сделать? (а + n)
— Как потом ответить на вопросы задачи? ((а + n): 2 — большее число, (а + n): 2-n — меньшее число.)
Вывод: Итак, мы нашли два пути решения таких задач по сумме и разности: найти сначала удвоенное меньшее число — вычитанием, либо найти сначала удвоенное большее число-сложением. На доске сопоставлены оба пути решения:
1 способ 2 способ
(а-n):2 (а + n):2
(a-n):2 + n (а + n):2 – n
4. Физкультминутка.
5. Первичное закрепление.
Учащиеся работают с учебником-тетрадью. Задания решаются с комментированием, решение записывается на печатной основе.
а) — Прочитайте про себя задачу № 6 (а), стр. 7.
— Что нам известно в задаче и что нужно найти? (Нам известно, что в двух классах 56 человек, причем в 1 классе на 2 человека больше, чем во втором. Нам надо найти количество учащихся в каждом классе.)
— “Оденьте” схему и проанализируйте задачу. (Нам известна сумма — 56 человек, и разность — 2 ученика. Сначала мы найдем удвоенное меньшее число: 56 – 2 = 54 человека. Затем узнаем, сколько учащихся во втором классе: 54: 2 = 27 человек. Теперь узнаем, сколько учащихся в первом классе — 27 + 2 = 29 человек.)
— Как по-другому найти, сколько учащихся в первом классе? (56 – 27 = 29 человек.)
— Как проверить, правильно ли решена задача? (Сосчитать сумму и разность: 27 + 29 = 56, 29 – 27 = 2.)
— Как по-другому можно было решить задачу? (Найти сначала число учеников в первом классе, и из него вычесть 2.)
б) — Прочитайте про себя задачу № 6 (б), стр. 7. Проанализируйте, какие величины известны, а какие — нет и придумайте план решения.
После минутного рассуждения в командах выступает представитель той команды, которая раньше готова. Устно разбираются оба способа решения задачи. После обсуждения каждого способа открывается готовый образец записи решения и сравнивается с ответом ученика:
I способ II способ
1) 18 – 4= 14 (кг) 1) 18 + 4 = 22(кг)
2) 14:2 = 7 (кг) 2) 22: 2 = 11 (кг)
3) 18 – 7 = 11 (кг) 3) 11 – 4 = 7 (кг)
6. Самостоятельная работа с проверкой в классе.
Учащиеся по вариантам решают на печатной основе задание № 7, стр. 7 (I вариант — № 7 (а), II вариант — № 7 (б)).
№ 7 (а), стр. 7.
I способ II способ
1) 248-8 = 240(м.) 1) 248 +8 = 256(м.)
2) 240:2=120(м.) 2) 256:2= 128 (м.)
3) 120 + 8= 128 (м.) 3) 128-8= 120(м.)
Ответ: 120 марок; 128 марок.
№ 7(6), стр. 7.
I способ II способ
1) 372+ 12 = 384 (отк.) 1) 372-12 = 360 (отк.)
2) 384:2= 192 (отк.) 2) 360:2= 180 (отк.)
3) 192 – 12 =180 (отк.) 3)180+12 = 192 (отк.)
Ответ: 180 открыток; 192 открытки.
Проверка — по готовому образцу на доске.
7. Решение задач на повторение.
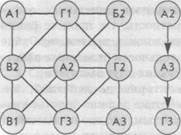
Каждая команда получает табличку с заданием: “Найти закономерность и вписать вместо знаков вопроса нужные числа”.
1 команда:
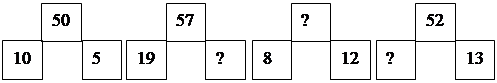
2 команда:
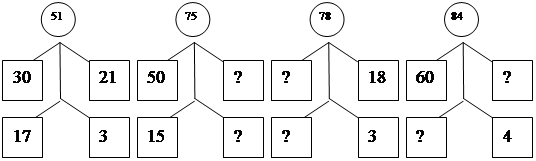
3 команда:
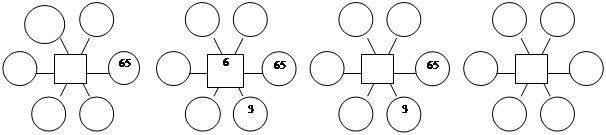
Капитаны команд отчитываются о результатах работы команд.
8. Итог урока.
— Объясните, как вы рассуждаете при решении задач, если выполняются следующие операции:
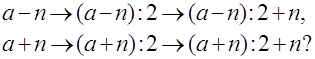
9. Домашнее задание.
Придумайте свою задачу нового типа и решите ее двумя способами.
Тема: СРАВНЕНИЕ УГЛОВ.
4 класс, 3 ч. (1-4)
Цель: 1) Повторить понятия: точка, луч, угол, вершина угла (точка), стороны угла (лучи).
2) Познакомить учащихся со способом сравнения углов с помощью непосредственного наложения.
3) Повторить задачи на части, отрабатывать решение задач на нахождение части от числа.
4) Развивать память, мыслительные операции, речь, познавательный интерес, исследовательские способности.
Ход урока:
Похожие работы
... задания и методические рекомендации по их использованию. Практическая значимость методических рекомендаций - в использовании их начинающими учителями школы первой ступени обучения для формирования учебно-исследовательской деятельности младших школьников. СПИСОК ЛИТЕРАТУРЫ 1. Антоненко, Т. Е. Приемы занимательности на уроках математики [Текст] / Т. Е. Антоненко // Начальная школа. 2008. №4 ...
... Компьютер в жизни младшего школьника. Результаты констатирующего этапа эксперимента. Мышление младшего школьника отличается от мышления дошкольника Во-первых, более высокими темпами развития, во-вторых, существенными структурными и качественными преобразованиями, происходящими в самих интеллектуальных процессах. В младшем школьном возрасте под влиянием учения как ведущей деятельности активно ...
... научного знания, с принципами построения научных теорий в единстве и противоположности математики и естественных и гуманитарных наук, с критериями истинности в разных формах человеческой деятельности. Заключение В исследовании внимание уделяется поиску конкретных новых событий и явлений и последовательному изложению выверенных фактов истории развития методики преподавания математики в России
... «Сравни свой ответ с текстом», «Найди ошибки» и др.). Обновление начальной школы означает переход с приоритета репродуктивной и инструктивной деятельности на приоритет поисков-исследовательский. В учебно-методическом комплекте «Начальная школа XXI века» это достигается методикой, при которой школьник осваивает принципиально другую роль – не просто «зритель», «слушатель», «репродуктор», а « ...



0 комментариев