Решение примеров на вычитание двузначных чисел без пере­хода через разряд

2.2. Решение примеров на вычитание двузначных чисел без пере­хода через разряд.

Посмотрим, кто лучше умеет решать эти примеры! Что интерес­ного в разностях: *9-64, 7*-54, *5-44,

 3*-34, *1-24?

Примеры лучше расположить один под другим. Дети должны заметить, что в уменьшаемом одна цифра неизвестна; неизвестные десятки и единицы чередуются; все известные цифры в уменьшаемом — нечетные, идут в порядке убывания: в вычитаемом количество десят­ков уменьшается на 1, а количество единиц не изменяется.

— Разгадайте уменьшаемое, если известно, что разность между цифрами, обозначающими десятки и единицы, равна 3. (В 1-м примере — 6 д., 12 д. взять нельзя, так как в разряд можно поставить только одну цифру; во 2-м — 4 ед., так как 10 ед. не подходят; в 3-м — 6 д., 3 д. взять нельзя, так как уменьшаемое должно быть больше вычитаемого; аналогично в 4-м — 6 ед., а в5-м — 4 д.)

Учитель раскрывает закрытые цифры и просит детей решить примеры:

69 — 64. 74 — 54, 85 — 44. 36 — 34, 41 — 24.

Для 2-3 примеров алгоритм вычитания двузначных чисел про­говаривается вслух: 69 — 64 =. Из 9 ед. вычитаем 4 ед., получаем 5 ед. Из 6 д. вычитаем 6 д., получаем О д. Ответ: 5.

2.3. Постановка проблемы. Целеполагание.

При решении последнего примера дети испытывают затруднение (возможны различные ответы, некоторые вообще не смогут решить): 41-24 = ?

Цель нашего урока — изобрести прием вычитания, который по­может нам решить этот пример и подобные ему примеры.

3. “Открытие” детьми нового знания.

Дети выкладывают модель примера на парте, и на демонстраци­онном полотне:

Как вычесть двузначные числа? (Из десятков вычесть десятки, а из единиц — единицы.)

Почему же здесь возникла трудность? (В уменьшаемом не хвата­ет единиц.)

Разве у нас уменьшаемое меньше вычитаемого? (Нет, уменьшае­мое больше.)

Где же спрятались единицы? (В десятке.)

Что надо сделать? (1 десяток заменить 10 единицами. — Открытие!)

 Молодцы! Решите пример.

Дети заменяют в уменьшаемом треугольник-десяток треугольни­ком, на котором нарисовано 10 единиц:

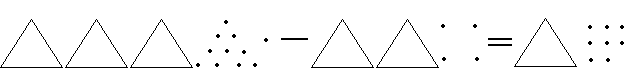
- 11е -4е = 7е, Зд-2д=1д. Всего получилось 1 д. и 7 е. или 17.

Итак. “Саша” предложил нам новый прием вычислений. Он заключается в следующем: раздробить десяток и взять из него недостающие единицы. Поэтому наш пример мы могли бы запи­сать и решить так (запись комментируется):

 _*10

_ 41

 24

 17

А как выдумаете, о чем всегда надо помнить при использовании это­го приема, где возможна ошибка? (Число десятков уменьшается на 1.)

4. Физкультминутка.

5. Первичное закрепление.

1) № 1, стр. 16.

— Прокомментируйте первый пример по образцу:

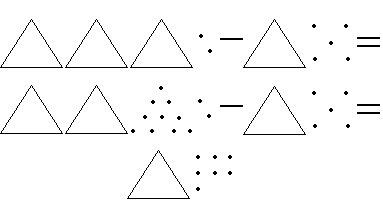
— 32 — 15. Из 2 ед. нельзя вычесть 5 ед. Дробим десяток. Из 12 ед. вычитаем 5 ед., а из оставшихся 2 дес. вычитаем 1 дес. Получаем 1 дес. и 7 ед., то есть 17.

— Решите следующие примеры с объяснением.

Дети дорисовывают графические модели примеров и одновремен­но комментируют решение вслух. Линиями соединяют рисунки с ра­венствами.

2) № 2, стр. 16

Еще раз четко проговаривается решение и комментирование примера в столбик:

 _81 _82 _83 _84 _85 _86

29 29 29 29 29 29

Пишу: единицы под единицами, десятки под десятками.

Вычитаю единицы: из 1 ед. нельзя вычесть 9 ед. Занимаю 1 д. и ставлю точку. 11-9 = 2 ед. Пишу под единицами.

Вычитаю десятки: 7-2 = 5 дес.

Ответ: 52.

Дети решают и комментируют примеры до тех пор, пока не заме­тят закономерность (обычно 2-3 примера). На основании установ­ленной закономерности в оставшихся примерах они записывают ответ, не решая их.

3) № 3, стр. 16.

— Сыграем в игру “Угадай-ка”:

82 — 6 41 -17 74-39 93-45

82-16 51-17 74-9 63-45

Дети записывают и решают примеры в тетради в клетку. Сравни­вая их. они видят, что примеры взаимосвязаны. Поэтому в каждом столбике решается только первый пример, а в остальных ответ угадывается при условии, что дано верное обоснование и все с ним согласились.

6. Самостоятельная работа с проверкой в классе.

Учитель предлагает детям списать с доски в столбик примеры на новый вычислительный прием

98-19, 64-12, 76 — 18, 89 — 14, 54 — 17.

Дети записывают в тетради в клетку нужные примеры, а затем проверяют правильность своих записей по готовому образцу:

_98 _76 _54

19 18 17

Затем они самостоятельно решают записанные примеры. Через 2-3 мин учитель показывает правильные ответы. Дети их сами проверяют, отмечают правильно решенные примеры плюсом, исправ­ляют допущенные ошибки.

— Найдите закономерность. (Цифры в уменьшаемых записаны по порядку от 9 до 4, вычитаемые сами идут в порядке уменьшения и т.д.)

— Напишите свой пример, который продолжал бы эту закономер­ность.

7. Задачи на повторение.

Дети, которые справились с самостоятельной работой, придумы­вают и решают задачи в тетрадях, А те, кто допустил ошибки, дорабатывают ошибки индивидуально вместе с учителем или консуль­тантами. затем решают самостоятельно еще 1-2 примера по новой теме.

— Придумайте задачу и решите по вариантам:

1вариант 2вариант

— Выполните взаимопроверку. Что заметили? (Ответы в задачах одинаковые. Это взаимообратные задачи.)

8. Итог урока.

Какие примеры учились решать?

Можете ли теперь решать пример, который вызвал трудности в начале урока?

Придумайте и решите такой пример на новый прием!

Дети предлагают несколько вариантов. Выбирается один. Дети. записывают и решают его в тетрадь, а кто-нибудь один из детей — на доске.

9. Домашнее задание.

№ 5, стр. 16. (Разгадать название сказки и автора.)

Составить свой пример на новый вычислительный прием и решить его графически и в столбик.

Тема: УМНОЖЕНИЕ НА 0 И НА 1.

2кл., 2ч. (1-4)

Цель: 1) Ввести частные случаи умножения с 0 и 1.

2) Закрепить смысл умножения и переместительное свой­ство умножения, отрабатывать вычислительные навыки,

умение “читать”блок-схемы.

3) Развивать внимание, память, мыслительные операции, речь, творческие способности, интерес к математике.

Ход урока:

1. Организационный момент.

2. Постановка учебной задачи.

2.1. Задания на развитие внимания.

На доске и на столе у детей двуцветная картинка с числами:

 

	2	5		8
10			4
(синий)   (красный)	3			5
1		9	6

 

— Что интересного в записанных числах? (Записаны разными цве­тами; все “красные” числа — четные, а “синие” — нечетные.)

— Какое число лишнее? (10 — круглое, а остальные нет; 10 — дву­значное, а остальные однозначные; 5 — повторяется два раза, а осталь­ные — по одному.)

— Закрою число 10. Есть ли лишнее среди остальных чисел? (3 — у него нет пары до 10, а у остальных есть.)

— Найдите сумму всех “красных” чисел и запишите ее в красном квадрате. (30.)

— Найдите сумму всех “синих” чисел и запишите ее в синем квад­рате. (23.)

— На сколько 30 больше, чем 23? (На 7.)

— На сколько 23 меньше, чем 30? (Тоже на 7.)

— Каким действием искали? (Вычитанием.)

2.2. Задания на развитие памяти и речи. Актуализация знаний.

а) —Повторите по порядку слова, которые я назову: слагаемое, сла­гаемое, сумма, уменьшаемое, вычитаемое, разность. (Дети пытаются воспроизвести порядок слов.)

— Компоненты каких действий назвали? (Сложение и вычитание.)

— С каким новым действием мы познакомились? (Умножение.)

— Назовите компоненты умножения. (Множитель, множитель, про­изведение.)

— Что обозначает первый множитель? (Равные слагаемые в сумме.)

— Что обозначает второй множитель? (Число таких слагаемых.)

Запишите определение умножения.

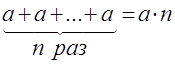
б) —Рассмотрите записи. Какое задание будете выполнять?

12 + 12 + 12 + 12 + 12

33 + 33 + 33 + 33

а + а + а

(Заменить сумму произведением.)

Что получится? (В первом выражении 5 слагаемых, каждый из которых равен 12, поэтому оно равно

 12 • 5. Аналогично — 33 • 4, а • 3)

в) — Назовите обратную операцию. (Заменить произведение суммой.)

— Замените произведение суммой в выражениях: 99 — 2. 8 • 4. Ь • 3. (99 + 99, 8 + 8 + 8 + 8, b+b+b).

г) На доске записаны равенства:

81+81=81–2

21• 3 = 21+22 + 23

44 + 44 + 44 + 44 = 44 + 4

17 + 17-17 + 17-17 = 17 • 5

Учитель рядом с каждым равенством помещает картинки соот­ветственно цыпленка, слоненка, лягушонка и мышонка.

— Зверюшки лесной школы выполняли задание. Правильно ли они его выполнили?

Дети устанавливают, что слоненок, лягушонок и мышонок ошиб­лись, объясняют, в чем их ошибки.

д) — Сравните выражения:

8 – 5... 5 – 8 34 – 9… 31 • 2

5 • 6... 3 • 6 а – 3... а • 2 + а

(8 • 5 = 5 • 8, так как от перестановки слагаемых сумма не изменя­ется; 5 • 6 > 3 • 6, так как слева и справа по 6 слагаемых, но слева слага­емые больше; 34 • 9 > 31 — 2. так как слева слагаемых больше и сами слагаемые больше; а • 3 = а • 2 + а, так как слева и справа по 3 слагае­мых, равных а.)

— Какое свойство умножения использовали в первом примере? (Переместительное.)

2.3. Постановка проблемы. Целеполагание.

Рассмотрите картинку. Верны ли равенства? Почему? (Верны, так как сумма 5 + 5 + 5= 15. потом в сумме становится на одно слагае­мое 5 больше, и сумма увеличивается на 5.)

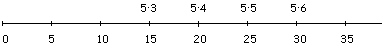
5 • 3 = 15 5 • 5 = 25

5 • 4 = 20 5 • 6 = 30

— Продолжите эту закономерность направо. (5 • 7 = 35; 5 • 8 = 40...)

— Продолжите ее теперь налево. (5 • 2 = 10; 5 • 1=5; 5 • 0 = 0.)

— А что означает выражение 5 • 1? 5 • 0? (? Проблема!) Итог обсуждения:

— В нашем примере было бы удобно считать, что 5 • 1 = 5, а 5 • 0 = 0. Однако выражения 5 • 1 и 5 • 0 не имеют смысла. Мы можем условиться считать эти равенства верными. Но для этого надо проверить, не нарушим ли мы переместительное свойство умножения. Итак, цель нашего урока — установить, сможем ли мы считать равенства 5 • 1 = 5 и 5 • 0 = 0 верными? — Проблема урока!

3. “Открытие” детьми нового знания.

1) № 1, стр. 80.

а) — Выполните действия: 1 • 7, 1 • 4, 1 • 5.

Дети решают примеры с комментированием в учебнике-тетради:

1 • 7 = 1 + 1 + 1 + 1 + 1 + 1 + 1 = 7

1 • 4 = 1 + 1 + 1 + 1 = 4

1 • 5 = 1 + 1 + 1 + 1 +1 = 5

— Сделайте вывод: 1 • а — ? (1 • а = а.) Учитель выставляет карточку: 1 • а = а

б) — Имеют ли смысл выражения 7 • 1, 4 • 1, 5 • 1? Почему? (Нет, так как в сумме не может быть одно слагаемое.)

— Чему они должны быть равны, чтобы не нарушалось переместительное свойство умножения? (7 • 1 тоже должно быть равно 7, поэтому 7 • 1 = 7.)

Аналогично рассматриваются 4 • 1 = 4; 5 • 1 = 5.

— Сделайте вывод: а • 1 = ? (а • 1 = а.)

Выставляется карточка: а • 1 = а. Учитель накладывает первую карточку на вторую: а • 1 = 1 • а = а.

— Совпадает наш вывод с тем, что у нас получилось на числовом луче? (Да.)

— Переведите это равенство на русский язык. (При умножении числа на 1 или 1 на число получается то же самое число.)

— Молодцы! Итак, будем считать:

а • 1 = 1 • а = а.

2) Аналогично исследуется случай умножения с 0 в № 4, стр. 80. Вывод — приумножении числа на 0 или 0 на число получается нуль:

а • 0 = 0 • а = 0.

— Сравните оба равенства: что вам напоминают 0 и 1?

Дети высказывают свои версии. Можно обратить их внимание на те образы, которые приведены в учебнике: 1 — “зеркальце”, 0 — “страш­ный зверь” или “шапка-невидимка”.

Молодцы! Итак, при умножении на 1 получается то же самое число (1 — “зеркальце”), а при умножении на 0 получается 0 (0 — “шапка-невидимка”).

4. Физкультминутка.

5. Первичное закрепление.

На доске записаны примеры:

23 • 1 = 0 • 925 = 364 • 1 =

1 • 89= 156 • 0 = 0 • 1 =

Дети решают их в тетради с проговариванием в громкой речи полученных правил, например:

3 • 1 = 3, так как при умножении числа на 1 получается то же самое число (1 — “зеркальце”), и т.д.

 2) № 1, стр. 80.

 а) 145 • х = 145; б) х • 437 = 437.

При умножении 145 на неизвестное число получилось 145. Значит, умножали на 1• х= 1. И т.д.

3) № 6, стр. 81.

 a) 8 • x = 0; б) х • 1= 0.

- При умножении 8 на неизвестное число получился 0. Значит, умножали на 0 • х = 0. И т.д.

6. Самостоятельная работа с проверкой в классе.

1) № 2, стр. 80.

1 • 729 = 956 • 1 = 1• 1 =

№5, стр. 81.

0 • 294 = 876 • 0 = 0 • 0 = 1 • 0 =

Дети самостоятельно решают записанные примеры. Затем по го­товому образцу проверяют свои ответы с проговариванием в громкой речи, отмечают правильно решенные примеры плюсом, исправляют допущенные ошибки. Те, кто допустил ошибки, получают аналогич­ное задание на карточке и дорабатывают индивидуально с учителем, пока класс решает задачи на повторение.