Навигация
8. Итог урока.
— Чему научились? Что повторили?
— Что понравилось? Что было трудно?
9. Домашнее задание: №№ 5, 12 (а), 16
Приложение 2Тренинг
Тема: “Решение уравнений”
Включает 5 заданий, в результате рассмотрения которых выстраивается весь алгоритм действий решения уравнений.
• В первом задании учащиеся, восстанавливая смысл действий сложения и вычитания, определяют, какой компонент выражает часть, а какой — целое.
• Во втором задании, определив, чем является неизвестное, дети выбирают правило для решения уравнения.
• В третьем задании учащимся предлагается три варианта решения одного и того же уравнения, причем ошибка кроется в одном случае в ходе решения, а в другом — в вычислении.
• В четвертом задании из трех уравнений нужно выбрать те, при решении которых используется одно и то же действие. Для этого ученик должен “пройти”весь алгоритм решения уравнений трижды.
• В последнем задании надо выбрать х в нестандартной ситуации, с которой дети еще не встречались. Таким образом, здесь проверяется глубина усвоения новой темы и способность ребенка применять изученный алгоритм действий в новых условиях.
Эпиграф урока: “Все тайное становится явным”. Приведем некоторые высказывания детей при подведении итогов в ресурсном круге:
— На этом уроке я запомнил, что целое находится сложением, а части — вычитанием.
— Все, что неизвестно, можно найти, если правильно выполнять действия.
— Я понял, что есть правила, которые нужно выполнять.
— Мы поняли, что не нужно ничего скрывать.
— Мы учимся, чтобы быть умными, чтобы неизвестное стало известным.
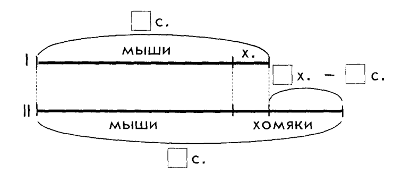
| Задание № 1 | Самост. выбор | Выбор в паре |
| Выбери уравнение, где х — целое: а) х+7=9 б) х–3 = 5 в) 9–х=4 | ||
| Задание № 2 | ||
| 5 + х = 7 Выбери правило: а) Чтобы найти часть, надо из целого вычесть другую часть. б) Чтобы найти часть, надо к целому прибавить другую часть. в) Чтобы найти целое, части надо сложить. | ||
| Задание № 3 | ||
| Выбери верное решение: а) х-2 = 6 б) х-2 = 6 в) х-2 = 6 х=6-2 х=2+6 х=6+2 х=4 х=9 х=8 | ||
| Задание № 4 | ||
| 5-х = 5 Чему равен х? а) 1 6) 0 в) 10 | ||
| Задание № 5 | ||
| Выбери уравнения с одинаковым решением: а)х+3 = 10 б) 10-х=3 в) х –3=10 |
| № задания | Верный выбор |
| 1 | б |
| 2 | а |
| 3 | в |
| 4 | а |
| 5 | а и б |
Приложение 3 Устные упражнения
Целью этого урока, является знакомство детей с понятием числового отрезка. В предложенных устных упражнениях не только идет работа по развитию мыслительных операций, внимания, памяти, конструктивных умений, не только отрабатываются навыки счета и ведется опережающая подготовка к изучению последующих тем курса, но и предлагается вариант создания проблемной ситуации, который может помочь учителю организовать при изучении данной темы этап постановки учебной задачи.
Тема: “Числовой отрезок”
Основная цель:
1) Познакомить с понятием числового отрезка, научить
одну единицу.
2) Закрепить навыки счета в пределах 4.
(К этому и последующим урокам дети должны иметь линейку длиной 20 см.) — Сегодня на уроке мы проверим ваши знания и смекалку.
[1] — “Потерялись”числа. Найдите их. Что можно сказать о месте каждого потерявшегося числа? (Например, 2 на 1 больше, чем 1, но на 1 меньше, чем 3.)
1... 3... 5... 7... 9
[2] — Установите закономерность в записи чисел. Продолжите вправо на одно число и влево на одно число:
... 3 5 7...
[3] — Восстановите порядок. Что вы можете сказать о числе 3?
1 2 3 4 5 6 7 8 9 10
[4]-Разбейте квадраты на части по цвету:
|
| |||||||
|
| |||||||
З+С=К 1+3=
+= +=
К-З=К 4-1=
-= -=
— Как обозначены все фигуры? Как обозначены части? Почему?
— Вставьте в “окошки”пропущенные буквы и цифры. Объясните свое решение.
— Что обозначают равенства 3 + С = К и К — 3 = С? Какие числовые равенства им соответствуют?
— Назовите целое и части в числовых равенствах.
— Как найти целое? Как найти часть?
— Сколько зеленых квадратов? Сколько синих?
— Каких квадратов больше — зеленых или синих — и на сколько? Каких квадратов меньше и на сколько? (Ответ можно пояснить на рисунке, составляя пары.)
— По какому еще признаку можно разбить на части эти квадраты? (По размеру — большие и маленькие.)
— На какие части тогда разобьется число 4? (2 и 2.)
[5] — Составьте два треугольника из 6 палочек.
— А теперь составьте два треугольника из 5 палочек.
— Уберите 1 палочку так, чтобы получился четырехугольник.
![]()
[6] — Назовите значения числовых выражений:
3 + 1 = 2-1 = 2 + 2 =
1 + 1 = 2 + 1 = 1 + 2 + 1 =
— Какое выражение “лишнее”? Почему? (“Лишним”может быть выражение 2—1, так как это разность, а остальные суммы; в выражении 1 + 2 + 1 три слагаемых, а в остальных — два.)
— Сравните выражения в первом столбике.
В случае затруднения можно задать наводящие вопросы:
— Что общего в этих числовых выражениях? (Одинаковый знак действия, второе слагаемое меньше первого и равно 1.)
— Чем они отличаются? (Разные первые слагаемые; во втором выражении оба слагаемых равны, а в первом — одно слагаемое на 2 больше другого.)
[7] — Задачи в стихах (решение задач обосновывается):
Два мяча у Ани, два мяча у Тани. (Ищем целое. Чтобы найти
Два мяча да два, малыш, целое, части надо сложить:
Сколько их, сообразишь? 2 + 2 = 4.)
Четыре сороки пришли на уроки. (Ищем часть. Чтобы найти
Одна из сорок не знала урок. часть, надо из целого вычесть
Сколько прилежно трудилось сорок? другую часть: 4 -1 = 3.)
[8] — Сегодня нас ждет встреча с нашими любимыми героями: Удавом, Мартышкой, Слоненком и Попугаем. Удав очень хотел измерить свою длину. Все попытки Мартышки и Слоненка ему помочь были напрасны. Беда их была в том, что они не умели считать, не умели складывать и вычитать числа. И вот сообразительный Попугай посоветовал измерить длину удава своими шагами. Он сделал первый шаг, и все хором закричали... (Один!)
Учитель выкладывает на фланелеграфе красный отрезок и выставляет в его конце цифру 1. Ученики рисуют в тетради красный отрезок длиной 3 клетки и записывают цифру 1. Аналогично достраиваются синий, желтый и зеленый отрезки, каждый по 3 клетки. На доске и в тетрадях учеников появляется цветной рисунок — числовой отрезок:
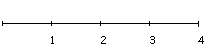
— Одинаковые ли шаги делал Попугай? (Да, все шаги равны.)
— Что показывает каждое число? (Сколько сделано шагов.)
— Как изменяются числа при движении вправо, влево? (При движении на 1 шаг вправо — увеличиваются на 1, а при движении на 1 шаг влево — уменьшаются на 1.)
Далее можно поработать с линейкой (5 + 1, 8 + 1, 12 + 1, 15 + 1, 18 + 1,…; 6 – 1, 8 – 1, 10 – 1, 14 – 1, 16 – 1...), а затем перейти к заданиям №№ 1—3, стр. 36 учебника (урок 24).
Материал устных упражнений не должен использоваться формально — “все подряд”, а должен соотноситься с конкретными условиями работы — уровнем подготовки детей, их количеством в классе, технической оснащенностью кабинета, уровнем педагогического мастерства учителя и т. д. Чтобы использовать этот материал правильно, в работе необходимо руководствоваться следующими принципами.
1. Обстановка на уроке должна, быть спокойной и доброжелательной. Нельзя допускать “гонки”, перегрузки детей — лучше разобрать с ними одно задание полноценно и качественно, чем семь, но поверхностно и сумбурно.
2. Формы работы необходимо разнообразить. Они должны меняться каждые 3-5 мин — коллективный диалог, работа с предметными моделями, карточками или кассой цифр, математический диктант, работа в парах, самостоятельный ответ у доски и т. д. Продуманная организация урока позволяет существенно увеличить объем материала, который может быть рассмотрен с детьми без перегрузки.
3. Введение нового материала должно начинаться не позже чем на 10-12-й минуте урока. Упражнения, предваряющие изучение нового, должны быть нацелены главным образом на актуализацию тех знаний, которые необходимы для его полноценного усвоения.
Похожие работы
... задания и методические рекомендации по их использованию. Практическая значимость методических рекомендаций - в использовании их начинающими учителями школы первой ступени обучения для формирования учебно-исследовательской деятельности младших школьников. СПИСОК ЛИТЕРАТУРЫ 1. Антоненко, Т. Е. Приемы занимательности на уроках математики [Текст] / Т. Е. Антоненко // Начальная школа. 2008. №4 ...
... Компьютер в жизни младшего школьника. Результаты констатирующего этапа эксперимента. Мышление младшего школьника отличается от мышления дошкольника Во-первых, более высокими темпами развития, во-вторых, существенными структурными и качественными преобразованиями, происходящими в самих интеллектуальных процессах. В младшем школьном возрасте под влиянием учения как ведущей деятельности активно ...
... научного знания, с принципами построения научных теорий в единстве и противоположности математики и естественных и гуманитарных наук, с критериями истинности в разных формах человеческой деятельности. Заключение В исследовании внимание уделяется поиску конкретных новых событий и явлений и последовательному изложению выверенных фактов истории развития методики преподавания математики в России
... «Сравни свой ответ с текстом», «Найди ошибки» и др.). Обновление начальной школы означает переход с приоритета репродуктивной и инструктивной деятельности на приоритет поисков-исследовательский. В учебно-методическом комплекте «Начальная школа XXI века» это достигается методикой, при которой школьник осваивает принципиально другую роль – не просто «зритель», «слушатель», «репродуктор», а « ...



0 комментариев