Навигация
1. Организационный момент.
2. Постановка учебной задачи.
а) — Продолжите ряд:
1) 3, 4, 6, 7, 9, 10,...; 2) 2, ½, 3, 1/3,...; 3) 824, 818, 812,...
б) — Вычислите и расположите в порядке убывания:
[И] 60-8 [Л] 84-28 [Ф] 240: 40 [А] 15 — 6
[Г] 49 + 6 [У] 7 • 9 [Р] 560: 8 [Н] 68: 4
Зачеркните 2 лишние буквы. Какое слово получилось? (ФИГУРА.)
в) — Назовите фигуры, которые вы видите на рисунке:

![]()
![]()
![]()
Какие фигуры можно неограниченно продолжить? (Прямую, луч, стороны угла.)
Я соединяю центр окружности с точкой, лежащей на окружности, Что получилось? (Отрезок, называется радиусом.)
Какая из ломаных является замкнутой, а какая — нет?
Какие еще плоские геометрические фигуры знаете? (Прямоугольник, квадрат, треугольник, пятиугольник, овал и т.д.) Пространственные фигуры? (Параллелепипед, куб. шар, цилиндр, конус, пирамида и т.д.)
Какие бывают виды углов? (Прямые, острые, тупые.)
Покажите карандашами модель острого угла, прямого, тупого.
Чем являются стороны угла — отрезками или лучами?
Если продолжить стороны угла, то получится тот же угол или другой?
г) № 1, стр. 1.
Дети должны определить, что у всех углов на рисунке сторона, образованная большой стрелкой, общая. Угол тем больше, чем больше “раздвинуты” стрелки.
д) № 2, стр. 1.
Мнения детей о соотношении между углами обычно бывает разным. Это служит основой создания проблемной ситуации.
3. “Открытие” детьми нового знания.
У учителя и детей модели углов, вырезанные из бумаги. Детям предлагается исследовать ситуацию и найти способ сравнения углов.
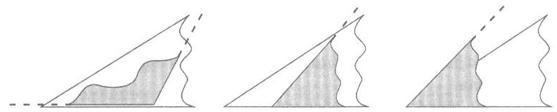
Они должны догадаться, что первые два способа не подходят, так как при продолжении сторон углов ни один из углов не оказывается внутри другого. Затем на основе третьего способа — “который подходит”, выводится правило сравнения углов: углы надо наложить один на другой так, чтобы одна сторона их совпадала. — Открытие!
Учитель подводит итог обсуждению:
Для сравнения двух углов можно наложить их так, чтобы одна сторона у них совпала. Тогда меньше тот угол, сторона которого оказалась внутри другого угла.
Полученный вывод сравнивается с текстом учебника на стр. 1.
4. Первичное закрепление.
Задание № 4, стр. 2 учебника решается с комментированием, вслух проговаривается правило сравнения углов.
В задании № 4, стр. 2 углы надо сравнить “на глаз” и расположить их в порядке возрастания. Имя фараона — ХЕОПС.
5. Самостоятельная работа с проверкой в классе.
Учащиеся самостоятельно выполняют практическую работу в № 3, стр. 2, затем в парах объясняют, как они наложили углы. После этого 2-3 пары объясняют решение всему классу.
6. Физкультминутка.
7. Решение задач на повторение.
1) — У меня есть трудное задание. Кто хочет попробовать его решить?
Два добровольца за время математического диктанта вместе должны придумать решение задачи: “Найти 35% от 4/7 числа х”.
2) Математический диктант записан на магнитофоне. Двое записывают задание на индивидуальных досках, остальные — в тетради “в столбик”:
- Найти 4/9 от числа а. (а: 9 • 4)
- Найти число, если его 3/8 составляют b. (b: 3 • 8)
- Найти 16% от с. (с: 100 •16)
- Найти число, 25 % которого составляют х. (х: 25 • 100)
- Какую часть число 7 составляет от числа у? (7/y)
- Какую часть високосного года составляет февраль? (29/366)
Проверка — по образцу решения на переносных досках. Ошибки, допущенные при выполнении задания, разбираются по схеме: устанавливается, что неизвестно — целое или часть.
3) Разбор решения дополнительного задания: (х: 7 • 4): 100 • 35.
Учащиеся проговаривают правило нахождения части от числа: чтобы найти часть от числа, выраженную дробью, можно это число разделить на знаменатель дроби и умножить на ее числитель.
4) № 9, стр. 3 — устно с обоснованием решения:
— а больше, чем 2/3, так как 2/3-правильная дробь;
— b меньше, чем 8/5, так как 8/5-неправильная дробь;
— 3/11 от с меньше, чем с, а 11/3 от с больше, чем с, поэтому первое число меньше второго.
5) №10, стр. 3. Первая строчка решается с комментированием:
— Чтобы найти 7/8 от 240, надо 240 разделить на знаменатель 8 и умножить на числитель 7. 240: 8 • 7 = 210
— Чтобы найти 9/7 от 56, надо 56 разделить на знаменатель 7 и умножить на числитель 9. 56: 7 • 9 = 72.
— 14% — это 14/100. Чтобы найти 14/100 от 4000, надо 4000 разделить на знаменатель 100 и умножить на числитель 14. 4000: 100 • 14 = 560.
Вторая строчка решается самостоятельно. Тот, кто заканчивает раньше, расшифровывает имя фараона, в честь которого была построена самая первая пирамида:
| 1072 | 560 | 210 | 102 | 75 | 72 |
| Д | Ж | О | С | Е | Р |
6) № 12(6), стр. 3
Масса верблюда 700 кг, а масса груза, который он несет на спине, составляет 40% массы верблюда. Какова масса верблюда вместе с грузом?
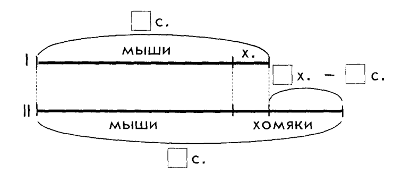
Учащиеся отмечают условие задачи на схеме и проводят ее самостоятельный анализ:
![]()
— Чтобы найти массу верблюда с грузом, надо к массе верблюда прибавить массу груза {ищем целое). Масса верблюда известна — 700 кг, а масса груза не известна, но сказано, что она составляет 40% от массы верблюда. Поэтому в первом действии находим 40% от 700 кг, а затем полученное число прибавляем к 700 кг.
Решение задачи с пояснениями записывается в тетрадь:
1) 700: 100 • 40 = 280 (кг) — масса груза.
2) 700 + 280 = 980 (кг)
Ответ: масса верблюда с грузом 980 кг.
Похожие работы
... задания и методические рекомендации по их использованию. Практическая значимость методических рекомендаций - в использовании их начинающими учителями школы первой ступени обучения для формирования учебно-исследовательской деятельности младших школьников. СПИСОК ЛИТЕРАТУРЫ 1. Антоненко, Т. Е. Приемы занимательности на уроках математики [Текст] / Т. Е. Антоненко // Начальная школа. 2008. №4 ...
... Компьютер в жизни младшего школьника. Результаты констатирующего этапа эксперимента. Мышление младшего школьника отличается от мышления дошкольника Во-первых, более высокими темпами развития, во-вторых, существенными структурными и качественными преобразованиями, происходящими в самих интеллектуальных процессах. В младшем школьном возрасте под влиянием учения как ведущей деятельности активно ...
... научного знания, с принципами построения научных теорий в единстве и противоположности математики и естественных и гуманитарных наук, с критериями истинности в разных формах человеческой деятельности. Заключение В исследовании внимание уделяется поиску конкретных новых событий и явлений и последовательному изложению выверенных фактов истории развития методики преподавания математики в России
... «Сравни свой ответ с текстом», «Найди ошибки» и др.). Обновление начальной школы означает переход с приоритета репродуктивной и инструктивной деятельности на приоритет поисков-исследовательский. В учебно-методическом комплекте «Начальная школа XXI века» это достигается методикой, при которой школьник осваивает принципиально другую роль – не просто «зритель», «слушатель», «репродуктор», а « ...



0 комментариев