Навигация
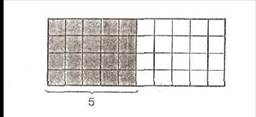
Сколько железнодорожных платформ потребуется для перевозки 183 контейнеров, если на одной платформе можно разместить не более 5 контейнеров
9. Сколько железнодорожных платформ потребуется для перевозки 183 контейнеров, если на одной платформе можно разместить не более 5 контейнеров.
10. Одна сторона треугольника равна 8 см., другая – 13см.
1) каким наименьшим целым числом сантиметров может быть длина третьей стороны?
2) каким наибольшим целым числом сантиметров может быть длина третьей стороны?
11.При каких значениях х точки графика функции у=3х+1.5 лежат выше точек графика функции у=-2х+1.
§3 Формирование алгоритма « Решение неравенств второй степени с одним неизвестным»
Цель:
· выработать умение решать неравенства второй степени с одним неизвестным и системы квадратных неравенств.
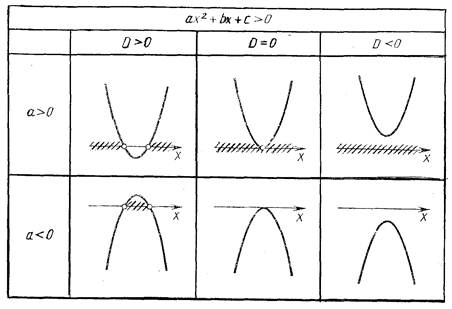
Решение квадратных неравенств – это традиционно обособленная часть исследования свойств квадратичной функции. Например, задача о решении неравенства х2-5х+6<0 может быть переформулирована в задачу о нахождении промежутков, на которых функция у =х2-5х+6 принимает отрицательные значения, а это легко решается с помощью эскиза графика. Этот способ фактически является строгим обоснованием графического способа.
Метод интервалов является логическим продолжением решения квадратных неравенств. Он позволяет решать более сложные неравенства, у которых левая часть – многочлен любой степень, представляемый в виде простых множителей, или дробь, у которой числитель и знаменатель также многочлены, разлагаемые на множители.
В результате изучения темы учащиеся должны уметь:
· решать квадратные неравенства с одной неизвестной графически и методом интервалов
Специфические действия:
1. Привидение неравенства к квадратному виду.
2. Решение квадратных уравнений.
3. Построение графиков функций (схематично).
4. Выполнение тождественных преобразований.
5. Определение знака выражения на соответствующих промежутках.
6. Алгоритм решения квадратных неравенств с одной переменной.
«Ядерным» материалом темы является:
1. Понятия «< » , « > » неравенство, решение неравенства решение системы неравенств, равносильных неравенств;
2. Свойства числовых неравенств, равносильных неравенств;
3. Алгоритм решения квадратных неравенств с одной переменной и решения системы неравенств.
4. Свойства графика квадратичной функции.
Рассмотрим работу с алгоритмом решения неравенств второй степени (графически) поэтапно. На первом этапе полезно актуализировать знания: нахождение корней квадратного трёхчлена, дискриминанта, изображение графиков квадратичных функций (схематично). После этого формулируем сам алгоритм. На втором этапе отрабатываем отдельные операции, входящие в алгоритм: изображение графиков функций, нахождение при каких значениях х функция принимает положительные, а при каких отрицательные значения. На третьем этапе применяем алгоритм при решении более сложных задач.
I. Введение алгоритма.
Рассмотрим введение алгоритма “решение неравенств второй степени с одним неизвестным” (графическим методом) с использованием обучающих самостоятельных работ.
1.Актуализация знаний
Обучающую самостоятельную работу проводим по новому материалу,
| |
| |
 но перед этим повторим ранее изученные понятия, которыми придётся воспользоваться.
но перед этим повторим ранее изученные понятия, которыми придётся воспользоваться. 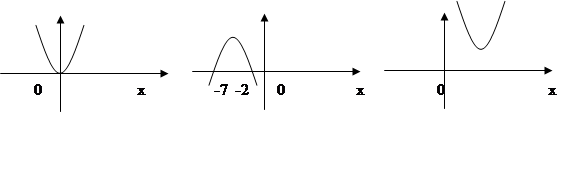 1. у у у
1. у у у
| |
а) Куда направлены ветви параболы?
b) Пересекает ли парабола ось ох, если да то сколько раз?
с) При каких х парабола принимает положительные значения?
d) При каких х парабола принимает отрицательные значения?
2. Изобразите схематично график функции.
· у=х2+5х-6
· у=-х2+4х-4
· у=3х2+4х+8
· у=0,1х2+3х-6
3. Изобразите схематично параболу, которая на
· промежутке (-∞;-3] убывает, а на промежутке [-3;+ ∞) возрастает;
· промежутке (-∞;6] возрастает, а на промежутке [6;+ ∞) убывает;
4. При каких значениях х , функция принимает положительные значения
· f(x)=-x2+4x-2;
· f(x)=3х2+2х-1;
5. При каких значениях х , функция принимает отрицательные значения
· f(x)=-х2+4х-1;
· f(x)=4x2+2x-1;
2. Открытие алгоритма учащимися под руководством учителя.
После этого начинается работа с объяснительным текстом. Каждый ученик самостоятельно изучает этот текст. Это предполагает активную работу мысли ученика. Текст составлен таким образом, чтобы учащиеся в меру возможностей самостоятельно выводили формулы, находили нужные приёмы решения задачи.
Если в левой части неравенства стоит квадратный трёхчлен, а в правой – нуль, то такое неравенство называют квадратным. Например, неравенства
2х2-3х+1≥0, -3х2+4х+5<0 являются квадратными.
Решением неравенства с одним неизвестным называется то значение неизвестного, при котором это неравенство обращается в верное числовое неравенство.
Решить неравенство – найти все его решения или установить, что их нет.
Решение неравенства второй степени с одной переменной можно рассматривать как нахождение промежутков, на которых соответствующая квадратичная функция принимает положительные и отрицательные значения.
Например, решим с помощью свойств графика квадратичной функции неравенство 2х2-х-1≤0
График квадратичной функции у=2х2-х-1 – парабола, ветви которой направлены вверх.
Найдём точки пересечения этой параболы с осью ох, для этого решим квадратное уравнение 2х2-х-1=0. Корни уравнения х1=1, х2=-0.5
Следовательно парабола пересекает ось ох в точках х1=1, х2=-0.5
Покажем схематично как расположена парабола в координатной плоскости.
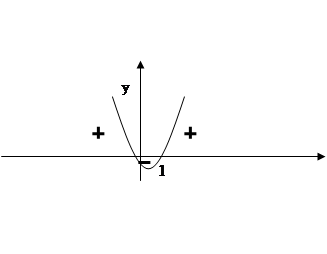
|
Из рисунка видно, что неравенству 2х2-х-1≤0 удовлетворяют те значения х, при которых значения функций равны нулю или отрицательны то есть те значения х при которых точки параболы лежат на оси ох или ниже этой оси. Из рисунка видно, что этими значениями являются все числа из отрезка
[-0.5;1].
Ответ: -0.5≤х≤1
График этой функции можно использовать и при решении других неравенств, которые отличаются от данного только знакомом неравенства, из рисунка видно, что:
1) решениями неравенства 2х2-х-1 < 0 являются числа интервала -0.5<х<1
2) решениями неравенства 2х2-х-1 > 0 являются все числа промежутков
х<-0.5 и х>1.
3) решениями неравенства 2х2-х-1 ≥ 0 являются все числа промежутков
х ≤-0.5 и х ≥ 1.
После работы с объяснительным текстом учащиеся получают «нулевые» задания. Они предназначены для самоконтроля и к ним предлагаются правильные ответы. Если ответы учеников не совпали с данными ответами, то придётся повторно прочитать объяснительный текст и снова выполнить «нулевые» задания, устранив ошибки.
10 Решите неравенства:
а) 4х2-5х+6х<0,2(10х2+15)
Похожие работы
... и содержательного обобщения свойств изучаемого предмета в форме учебного диалога. В процессе написания работы была проанализирована психолого- педагогическая и методическая литература по теме «Использование учебников математики при изучении табличного умножения и деления на 2 и 3», а также содержание учебных программ по математике, были сравнены учебники по математике Л.Г. Петерсон и М.И. Моро, ...
... на основе знания связи между результатом и компонентами арифметических действий (т.е. знания способов нахождения неизвестных компонентов). Эти требования программы определяют методику работы над уравнениями. 2. Методика изучения неравенств в старших классах 2.1 Содержание и роль линии уравнений и неравенств в современном школьном курсе математики Ввиду важности и обширности материала, ...
... и практическое использование различных форм уроков математики Для того чтобы доказать или опровергнуть, что использование различных форм уроков способствует улучшению качества знаний школьников по теме "Квадратные уравнения", были разработаны и проведены разнообразные формы уроков в 8 классе МОУ “Иштеряковская средняя общеобразовательная школа". При изучении темы были выбраны такие формы ...
... механизма для обеспечения эффективного перехода на различные способы транспортирования в зависимости от свойств материала и выполняемой технологической операции. Разработке методов кинематического анализа механизмов транспортирования ткани швейных машин и соответствующего этой задаче алгоритмического и программного обеспечения посвящены работы. [67],[71],[72]. В работе Ю.Ю.Щербаня и В.А.Горобца ...
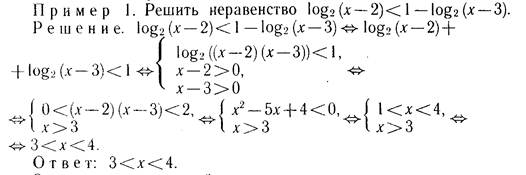

0 комментариев