Если Д<0, то уравнение не имеет корней;
Под алгоритмизацией обучения понимают алгоритмизацию деятельности учителя; составление и использование алгоритмов обучения
Избавьтесь от дробных чисел в неравенстве и где нужно раскройте скобки
Сколько железнодорожных платформ потребуется для перевозки 183 контейнеров, если на одной платформе можно разместить не более 5 контейнеров
Приведите неравенство к квадратному виду
Решите неравенства
Решите неравенство
Записать ответ
Неверно
Навигация
Решите неравенство
Применение алгоритмического метода при изучении неравенств
59195
знаков
4
таблицы
13
изображений
1. Решите неравенство.
1) 
2)
3)
4)
2. Найдите общее решение х2+6х-7 ≤ 0 и х2-2х-15 ≤ 0
3.Решите систему неравенств.
1)
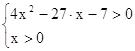
2)
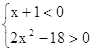
3)
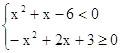
4.Катер должен не более чем за 4 часа пройти по течению реки 22,5км и вернуться обратно. С какой скоростью относительно воды должен идти катер, если скорость течения равна 3км/ч.
5.Решите неравенство методом интервалов.
1)
2)
3)
6.Решите неравенство.
1)
2)
3)
§4 Опытное преподавание.
Факультативное занятие в девятом классе (решение неравенств с параметром первой степени с одной неизвестной).
Цель:
применить алгоритмический метод при формировании умений и навыков в решении линейных неравенствах с параметрами.
Задачи:
· расширить кругозор учащихся;
· воспитание внимания, аккуратности, самостоятельности;
· осуществление взаимосвязи теории и практики;
· развитие памяти, логического мышления.
Решение задач с параметрами всегда вызывает большие трудности у учащихся. Причём часто учащиеся испытывают психологические трудности, «боятся» таких задач, так как не видят связи в их решении с решениями линейных неравенств с одной переменной.
Изучение линейных неравенств с параметром первой степени с одной неизвестной не возможно без умения решать линейные неравенства с одной переменной. Так как факультатив проводился в 9 классе, а линейные неравенства изучались в восьмом классе, то возникла необходимость актуализировать знания по решению линейных неравенств, вспомнить этапы их решения. Ученикам можно предложить следующее задание.
Решите неравенство 2(х+5)-3≥4+3х
Все решают у себя в тетрадях, а один ученик решает у доски. Запись ведёт в два столбика. Решение в одном столбика, а в другом записывают пояснения к своим действиям.
2х+7≥4+3х Раскрыли скобки в обеих частях неравенства
2х-3х≥4-2 Перенесли слагаемые, содержащие переменную в одну
часть, а не содержащую в другую.
-х≥2 Привели подобные члены в каждой части.
х≤-2 Разделили обе части неравенства на коэффициент при
переменной (учитывая его знак !).
Отметили соответствующие промежутки на
координатной прямой.
х
(-∞;-2] Записали числовой промежуток
После того как повторили этапы решения линейных неравенств с одной переменной, учитель предлагает на доске подробный разбор решения неравенства с параметром. Затем ученики вместе с учителем формулируют алгоритм решения линейных неравенств с параметром.
Пример 1. Рассмотрим решение неравенства (а-4)∙х<12
Чтобы найти х, обе части неравенства хочется разделить на (а-4). Однако теперь важно положительно, отрицательно или равно нулю выражение (а-4).
Определим знак выражения
|
|
|
Рассмотрим три случая:
a) а-4=0
b) а-4>0
c) а-4<0
1)если а-4=0
а=4, то неравенство примет вид 0х<12, которое справедливо для всех хR
2) a-4>0 a>4, то разделим обе части неравенства на положительное выражение (а-4), не меняя знак неравенства, получим х >
(используем свойство числового неравенства).
3) a-4<0a<4, то разделив обе части неравенства на отрицательное выражение и поменяв знак неравенства, получим х<.
Ответ:
если а=4, то х R;
если а>4, то х >;
если а<4, то х<.
Таким образом, после разобранного примера учитель формулирует алгоритм, опираясь на знания и умения, учащихся о решении линейных неравенств с одной переменной.
1. Раскрыть скобки в обеих частях неравенства (если есть дробные коэффициенты, то неравенство освободить от дробей).
2. Перенести слагаемые, содержащие переменную в одну часть, а не содержащие в другую.
3. Привести подобные члены в каждой части и получить один из 4 видов неравенств А(а)х<B(a) (**) , А(а)х≤B(a), А(а)х>B(a), А(а)х≥B(a), где х- переменная, А(а) и В(а) – функции параметра а.
4. Рассмотреть три случая:
1) Найти а, при которых А(а)=0, подставить в неравенство(**) вместо параметра а найденные решения и решить соответствующие неравенства.
2) Найти а, при которых А(а)>0, разделить неравенство(**) на А(а), не меняя его знак.
3) Найти а, при которых А(а)<0, разделить неравенство(**) на А(а), поменяв его знак.
Похожие работы
... и содержательного обобщения свойств изучаемого предмета в форме учебного диалога. В процессе написания работы была проанализирована психолого- педагогическая и методическая литература по теме «Использование учебников математики при изучении табличного умножения и деления на 2 и 3», а также содержание учебных программ по математике, были сравнены учебники по математике Л.Г. Петерсон и М.И. Моро, ...
... на основе знания связи между результатом и компонентами арифметических действий (т.е. знания способов нахождения неизвестных компонентов). Эти требования программы определяют методику работы над уравнениями. 2. Методика изучения неравенств в старших классах 2.1 Содержание и роль линии уравнений и неравенств в современном школьном курсе математики Ввиду важности и обширности материала, ...
... и практическое использование различных форм уроков математики Для того чтобы доказать или опровергнуть, что использование различных форм уроков способствует улучшению качества знаний школьников по теме "Квадратные уравнения", были разработаны и проведены разнообразные формы уроков в 8 классе МОУ “Иштеряковская средняя общеобразовательная школа". При изучении темы были выбраны такие формы ...
... механизма для обеспечения эффективного перехода на различные способы транспортирования в зависимости от свойств материала и выполняемой технологической операции. Разработке методов кинематического анализа механизмов транспортирования ткани швейных машин и соответствующего этой задаче алгоритмического и программного обеспечения посвящены работы. [67],[71],[72]. В работе Ю.Ю.Щербаня и В.А.Горобца ...
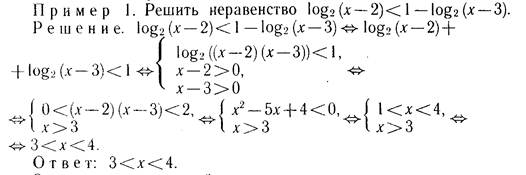
0 комментариев