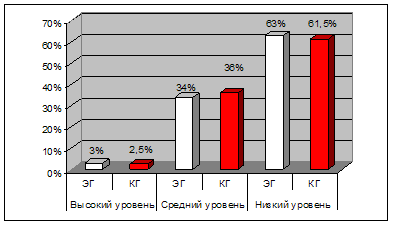
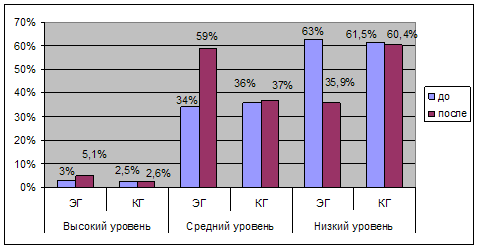
Все учащиеся без исключения не могут мысленно создать образ предмета и рассмотреть его с разных сторон «в воображении»

4.          Все учащиеся без исключения не могут мысленно создать образ предмета и рассмотреть его с разных сторон «в воображении».

5.         Как итогом всех этих фактов можно отметить то, что учащиеся больше предпочитают заниматься алгеброй, чем геометрией.

  2.2. Характеристика задач на построение.

В преподавании математики большое значение при­обретают вопросы, связанные с обучением учащихся геометрическим построениям (выполнение наиболее рас­пространенных геометрических построений и обучение решению задач на построение).

Решая задачи на построение, учащиеся приобретают первые теоретические и практические основы «графической грамотности», знакомятся с наиболее употребитель­ными приемами их решения, с инструментами, исполь­зуемыми в различных условиях работы (о чертежно-конструкторской практике, при разметке, при выполне­нии построений на местности). У них развиваются пространственное воображение, конструктивные способно­сти, сообразительность, изобретательность, т. е. такие качества, которые необходимы работникам многих про­фессий.

Доказательство правильности решения задачи и ее исследование способствуют лучшему усвоению учащими­ся теоретического материала, развитию их логического мышления.

Обучение геометрическим построениям в школе имело до последнего времени много недостатков. Так, уча­щиеся поздно знакомились с геометрическими построениями (в VI классе ими занимались лишь в конце учебного года). Приемы решения задач на построение часто не отвечали требованиям практики: как правило, изуча­лись построения, выполняемые только циркулем и линейкой, а другие чертежные инструменты практически не использовались; мало уделялось внимания распространенным построениям, хотя обоснование их соот­ветствовало программе по геометрии и целесообразность применения этих построений на уроках математики, чер­чения и других предметов не вызывала сомнения; при рассмотрении геометрических построений не уделялось должного внимания установлению связи между приема­ми построений (на бумаге, при разметке, на местности) и использованием соответствующих инструментов.

  2.2.1. Определение задачи на построение.

Задачей на построение называется предложение, ука­зывающее, по каким данным, какими средствами (инст­рументами) и какой геометрический образ (точку, пря­мую, окружность, треугольник, совокупность точек и т. д.) требуется найти (начертить, построить на плоскости, на­метить на местности и т. п.) так, чтобы этот образ удо­влетворял определенным условиям.

Будем считать средствами построения циркуль и одно­стороннюю линейку; вопрос о дополнении этих инстру­ментов чертежным прямоугольным треугольником будет рассмотрен далее.

Задача на построение может быть выражена с по­мощью чертежа-задания. Чертеж-задание включа­ет в себя данные элементы и требование задачи. Рассмот­рим примеры.

1. Построить треугольник по основанию а, углу при основании В=β и высоте на основание h_а (рис.6)

2. Построить окружность данного радиуса r, проходящую через две данные точки А и В (рис.7).

Чертеж-задание выделяет из элементов плоскости данные элементы. При этом возможны два случая: 1) дан­ные элементы являются уже построенными (пример 2, точки А и В), и в этом случае перемещение их по пло­скости невозможно (данные элементы определены по по­ложению); 2) данные элементы лишь могут быть постро­ены (пример 1 – отрезки а и h_а, угол В, пример 2 – от­резок r); в этом случае подразумевается, что элементы могут быть построены в «любом месте» плоскости (дан­ные элементы не определены по положению).

Решить задачу на построение при помощи циркуля и линейки – значит свести ее к конечной сово­купности пяти элементарных построений, которые заранее считаются выполнимыми:

1) построение прямой линии через две известные точки:

Дано: Дано:

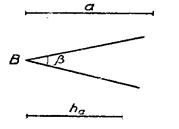
Построить треугольник Построить окружность

АВС радиуса r, проходящую

через точки А и В

Рис. 6 Рис. 7

2) построение точки пересечения двух известных пря­мых (если эта точка существует);

3) построение окружности известного радиуса с цент­ром в известной точке;

4) построение точек пересечения известной прямой и известной окружности (если эти точки существуют);

5) построение точек пересечения двух известных окружностей (если такие точки существуют).

Термин «известный элемент» означает, что этот элемент либо дан, либо получен в предыдущих построениях, либо выбран произвольно.

Сведения к каждой задаче к элементарным построениям практически неудобно, так как делает решение громоздким. Иногда удобнее сводить задачи к так называемым основным построениям. Выбор некоторых построений в качестве основных в известной мере произволен.

Характеристика чертежа-задания показывает, что за­дачи на построение делятся на два существенно различ­ных вида:

Задачи «метрические», в которых требуется построить геометрический образ по данным элементам, имеющим определенные размеры, но не определенными по положению на плоскости. Следовательно, и требуемый в задаче геометрический образ может занимать произволь­ное положение на плоскости (пример 1).

Задачи «положения», в которых построение требуемого геометрического образа выполняется на осно­ве данных элементов, из которых хотя бы один определен по положению на плоскости. Следовательно, и требуемый геометрический образ должен занимать определенное по­ложение на плоскости (относительно данных элементов, пример 2).

  2.2.2. Некоторые вопросы теории геометрических построений.

В теории геометрических построений каждый инстру­мент выполняет свойственную только ему операцию. Описание этой операции является его абстрактной характеристикой и дает возможность указать на те эле­менты чертежа, которые могут быть построены при од­нократном использовании того или иного инструмента.

Обычно на практике несколько «абстрактных» инст­рументов объединяются в один (например, чертежный треугольник является комбинацией односторонней ли­нейки, прямого и двух острых углов). Часто также один инструмент используется для выполнения двух (или не­скольких) совершенно различных операций (например, линейка используется для построения прямой, проходя­щей через две заданные точки, и общих касательных к двум данным окружностям). Это дает возможность зна­чительно сократить число используемых инструментов.

Укажем характерные операции для наиболее распро­страненных в школьной практике чертежных приборов и на те элементы чертежа, которые могут быть получены при однократном их использовании.

 Циркуль. Характерная для циркуля операция – проведение окружности данным (или произвольным) ра­диусом с центром в данной (или произвольной) точке.

Таким образом, циркулем могут быть построены:

а) окружность данного радиуса с центром в данной точке (радиус может быть задан двумя точками);

б) дуга окружности данного радиуса с центром в данной точке.

Линейка. Характерная операция для чертежной линейки – проведение прямой через две дан­ные точки.

На практике линей­кой пользуются также для построения к дан­ной окружности каса­тельной (рис. 8), проходящей через за­данную вне ее точку, и для построения общих внешних и внутренних касательных к двум окружностям.

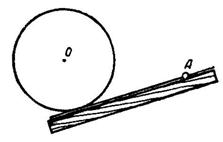
Рис. 8

Теоретически эти опе­рации так же строги, как и проведение прямой через две данные точки. Практическая точность в большинстве случаев вполне удовлетворительна. Этот прием часто используется в чертежных работах и при разметке. Итак, при помощи линейки могут быть построены:

а) прямая, проходящая через две данные точки;

б) отрезок прямой, ограниченный двумя данными точками;

в) луч, проходящий через данную точку и имеющий начало в другой данной точке;

г) касательная к данной окружности, проходящая через данную вне окружности точку;

д) внешние и внутренние касательные к двум данным окружностям.

Чертежный треугольник обладает всеми свойствами односторонней линейки. Следовательно, с помощью чертежного треугольника могут быть получены те же элементы, что и с помощью линейки, а также прямая, проходящая через данную точку и образующая с данной прямой угол, равный одному из углов чертежного треугольника.

Транспортир. Характерной операцией для тран­спортира является построение точки, лежащей на луче, проходящем через данную на прямой точку и образующем заданный угол с этой прямой (рис. 9).

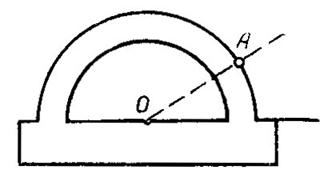
Рис. 9

Абстрактная характеристика каждого инструмента может быть использованы для выяснения вопроса о разрешимости задач на построение теми или ины­ми инструментами.

С этой целью в теорию геометрических построе­ний вводится понятие класса конструктивных элементов. К этому клас­су относятся все заданные элементы, а также: прямая, если она определяется двумя конструктивными точками; окружность, если она определяется конструктивным цен­тром и конструктивным радиусом (пара конструктивных точек); точка, лежащая на луче, проходящем через за­данную на конструктивной прямой точку и образующем с этой прямой заданный угол, и, наконец, точки, являю­щиеся пересечением конструктивных линий (прямых и окружностей).

Очевидно, что каждый набор инструментов имеет свой класс К конструктивных элементов.

На основании этого может быть установлен следую­щий критерий разрешимости задачи на построение.

Если искомый элемент (или элементы) принадлежит классу К, определяемому выбранным набором инстру­ментов, то задача является разрешимой при выполнении этими инструментами конечного числа операций.

Отсюда, естественно, следует, что возможность ис­пользования большого числа различных инструментов расширяет, вообще говоря, класс конструктивных эле­ментов и тем самым увеличивает число задач, допускающих точное решение.

В теории геометрических построений вопрос о необ­ходимости привлечения произвольных элементов для ре­шения (точного или приближенного) задач на построе­ние рассматривается в ряде работ; на основании тео­ремы, утверждающей, что при наличии среди заданных элементов двух различных точек класс конструктивных элементов, полученный при использовании циркуля и ли­нейки, образует счетное, всюду плотное множество, до­казывается, что любая задача на построение может быть решена при помощи циркуля и линейки без при­влечения произвольных элементов либо точно, либо при­ближенно с любой степенью точности, если среди задан­ных элементов имеются по крайней мере две различные точки.

  2.2.3. Выполнение геометрических построений.

Обучение учащихся геометрическим построениям преследует две цели: обучение выполнению собственно геометрических построений и обучение решению задач на построение.

Естественно, что каждому из этих вопросов в различ­ных классах должно быть уделено различное внимание. Рассмотрим первый из них.

В VI классе основное внимание обращается на обуче­ние учащихся выполнению простейших геометрических построений и их систематическому использованию при формировании и закреплении важнейших понятий: перпендикулярность и параллельность прямых, главнейшие линии в треугольнике, симметрия относительно прямой и т. д.

К концу VI класса учащиеся должны получить уже довольно прочные навыки в решении ряда конструктив­ных задач, включенных в программу VI класса, цен­ных с практической точки зрения и необходимых для дальнейшего изучения материала.

К этим построениям относятся различные приемы построения отрезка, равного данному, масштабной линейкой или циркулем и линейкой (немасштабной); действия над отрезками (в том числе деление отрезка пополам) при помощи масштабной линейки или циркуля и линейки (немасштабной); приближенное деление угла пополам циркулем; построение угла, равному данному, транспортиром или циркулем и линейкой; построение прямого угла чертежным треугольником; действия, производимые над углами малкой, транспортиром, цирку­лем и линейкой (немасштабной); построение парал­лельных и перпендикулярных прямых различными при­емами.

Умение фактически выполнять указанные выше по­строения является совершенно необходимым условием для дальнейшего успешного обучения решению кон­структивных задач, так как только при этом условии учащиеся, решая задачи, смогут уделить внимание со­держанию и методам их решения, а не только технике выполнения самого построения.

Кроме того, овладение рядом построений способствует лучшему усвоению новых понятий. Так, например, для усвоения таких важных понятий, как высота треугольника, симметрия относительно прямой и т.д., необходимо, чтобы учащиеся умели строить прямые углы, перпендикулярные прямые и т. д.

Правильно выполненный чертеж имеет большое зна­чение для отыскания плана решения задач на вычисление и доказательство, и наоборот, неверно выполненный чертеж часто не позволяет «увидеть» нужные соотноше­ния. Более того, неверный чертеж часто направляет мысль учащихся по неверному пути.

В VII классе перед учителем стоят более широкие задачи по изучению и использованию геометрических построений, в том числе решению задач на построение. Продолжается обучение выполнению некоторых новых построений и проводится систематическое закрепление приобретенных в VI классе умений; как и ранее, геомет­рические построения используются при формировании и закреплении геометрических понятий, а также для дока­зательства существования некоторых геометрических фигур. (Начало этой работы, доказательство существова­ния определяемых объектов, проводилось в VI классе; понятия медианы, биссектрисы, высоты треугольника, параллельных прямых вводились там на основе построе­ния.)

Новыми построениями для учащихся VII класса яв­ляются: построение центрально-симметричных фигур, деление отрезка на равные части, построение окружно­сти по трем ее точкам, деление дуг окружности на рав­ные часта, деление дуг и хорд окружности пополам, про­ведение касательной к окружности через данную точку.

Все эти построения, выполнение которых в большин­стве случаев основывается на материале, изученном в VI классе, используются затем при решении конструк­тивных задач. Необходимо, чтобы учащиеся умели фак­тически выполнять их при любом взаимном положении заданных элементов.

В VII классе продолжается формирование умений учащихся выбирать различные приемы построения в за­висимости от условия задачи. Так, например, перед ними может быть поставлен вопрос, каким способом они будут проводить через данную точку касательную к дан­ной окружности, если:

а) точка лежит вне окружности и центр окружности неизвестен,

б) точка лежит на окружности и центр окружности неизвестен,

в) точка лежит на окружности, а центр окружности находится вне чертежа.

Построение касательных для всех этих случаев уча­щиеся не должны заучивать. Они должны лишь пред­ставлять, как нужно поступить в зависимости от условия задачи, какие соотношения между искомыми и данными, элементами надо использовать для построения.

В VIII классе число новых построений весьма ограничено – это деление отрезка в данном отношении, по­строение фигур, подобных данным, построение углов по заданным значениям их тригонометрических функций и построение правильных многоугольников. Таким образом, основное внимание здесь уделяется закреплению ранее изученных построений и решению задач на построение.

  2.2.4. О некоторых вопросах методики обучения решению задач на построение.

При решении с учащимися задач на построение возникают большие методические трудности. Дело в том, что при этом обычно преследуют две цели; решить данную задачу и вместе с тем научить школьников решать задачи на построение вообще, т.е. познакомить их с общими подходами к решению задач, показать, как путем анализа искомой фигуры, рассуждений, предположений отыскивается решение задачи.

Эта вторая задача значительно сложней, чем первая, и ее реализация требует от учителя большом кропотли­вой и систематической работы, особенно в средней школе, так как решение задач на построение – совер­шенно новый для учащихся вид работы. Во многих слу­чаях отыскание хода решения новой задачи является для учащихся небольшим открытием и в то же время исследованием.

Трудность усугубляется еще и тем, что часто нахождение решения задачи представляет собой весьма сложный процесс, требующий от учащихся большого внимания. Для того чтобы эта работа протекала успешно, необходимо, чтобы учащиеся заинтересовались решением задач, чтобы они поняли, насколько интересна эта работа. Поэтому всегда следует поощрять проявление учащимися изобретательности, инициативы, самостоя­тельности в отыскании решения.

С первых уроков геометрии, подводя учащихся к решению задач на построение, надо обеспечивать им неко­торую самостоятельность, а тогда, когда это необходи­мо, направить мысль учащихся на желаемый путь. Иногда, может быть, даже следует создать у учащихся иллюзию самостоятельности с тем, чтобы придать им уверенность в работе, заинтересовать их решением за­дач.

Мера самостоятельности в работе, выполняемой уча­щимися, должна определяться учителем, исходя из их возраста, подготовки, сложности решаемой задачи.

  2.2.5. Введение задач на построение.

Продумывая систему работы по обучению школьников геометрическим построениям, особое внимание следует уделить методике обучения решению задач на построение.

Для подготовки учащихся к возможно более самостоятельному решению задач на построение целесооб­разно в ряде случаев вначале предлагать учащимся за­дачи подготовительного характера. Они могут быть как на построение, так и на вычисление, и на доказатель­ство. Ниже приводятся три примера использования вспомогательных задач.

Пример:

Через вершину данного угла провести прямую, образующую с его сторонами равные углы.

Угол АВС равен 62⁰. Через вершину угла про­ведена прямая МN, перпендикулярная его биссек­трисе. Вычислить углы, которые образует эта пря­мая со сторонами угла.

Пример:

Через точку Р, данную внутри угла АВС, про­вести прямую, отсекающую от сторон угла равные отрезки.

Стороны угла пересечены прямой, перпендику­лярной его биссектрисе. Доказать, что отрезки сторон угла, отсекаемые этой прямой, равны.

Пример:

Две точки А и В находятся по одну сторону прямой L. На прямой L найти такую точку С, что­бы сумма расстояний АС и ВС была наименьшей.

Отрезок АС перпендикулярен прямой L и де­лится в точке пересечения с этой прямой пополам. Точка В находится на прямой L. Доказать, что точ­ка В находится на одинаковом расстоянии от то­чек А и С.

Такая подготовительная работа важна в начале обу­чения решению задач потому, что у учащихся VI-VII классов еще очень слабы связи между различными фактами, изучаемыми в геометрии. Кроме того, на первых порах нельзя допускать нагромождения трудностей. Необходимо работу учащихся сделать насыщенной, но посильной.

Иногда полезно от решения практической задачи перейти к задаче на построение. Здесь некоторая сюжетная задача (а стало быть, более понятная) будет сведена к математической.

В некоторых случаях к одной и той же задаче полез­ло обращаться несколько раз, с тем чтобы показать уча­щимся различные способы ее решения.

В ряде случаев различные по содержанию практические задачи сводятся к одной и той же математической. Так, решение следующих двух задач сводится к реше­нию первой задачи предыдущего примера.

В каком месте следует построить переправу, чтобы расстояние от пункта А до пункта В было наименьшим (рис. 19).

Шириной реки в данном случае пренебрегаем.

Луч из источника света А отражает от экрана Е так, что отраженный луч проходит через точку В. Найти точку экрана, в которой отразился луч света.

Еще пример (первая задача – геометрическая, три последующие – практические):

 Две точки А и В расположены по одну сторону прямой МN. На этой прямой найти такую точ­ку С, чтобы АСМ = ВСN.

В какую точку нужно направить луч света из точки А, чтобы он, отразившись от непрозрачного экрана а, попал в точку В (рис 20)?

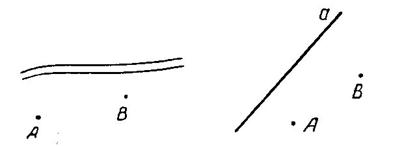
Рис. 19 Рис. 20

В какую точку нужно направить упругий шар А, чтобы он, отразившись от упругой стенки, прошел через точку В (рис. 20)?

К двум точкам А и В подвешена гибкая нерастяжимая нить, на которую надето тяжелое коль­цо. Найти положение равновесия кольца на нити.

Часто оказывается, что математическая задача весь­ма проста, но если вложить в нее практическое содержа­ние, то она становится недоступной. Поэтому полезно в VI–VIII классах рассматривать с учащимися примеры того, как различные практические задачи сводятся к одной и той же математической.

Большое образовательное значение имеет ознаком­ление учащихся с приборами, применяемыми на практи­ке при решении некоторых конструктивных задач. Обычно эта работа проводится после решении соответствующих задач на построение. Так, например, после рассмотрения свойства перпендикуляра, проведенного к хорде через ее середину, учащимся предлагается найти центр изображенной на чертеже окружности (возможный порядок решения задачи дан на рис. 21 и 22).

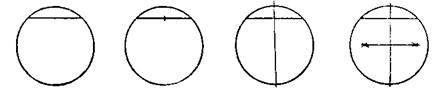
Рис. 21

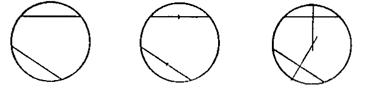
Рис. 22

2.2.6. Этапы решения задачи на построение.

Анализ.

Анализ – это важный этап решения задачи, так как здесь мы составляем план построения, по существу, находим решение. Устанавливаются такие зависимости между данными и искомыми элементами, которые дают возможность построить искомую фигуру. При обучении решению задач па построение целесообразно подчерки­вать аналогию, существующую между отысканием ре­шения задач по арифметике, алгебре и геометрии ни вычисление и доказательство и анализом задач на по­строение. Ученик не должен считать, что для нахождения решений задач на построение нужны совершенно новые приемы. Поэтому следует помочь ученикам увидеть ана­логию в применяемых приемах для отыскания решении задач на построение и задач из других дисциплин.

При решении задач по алгебре на составление и ре­шение уравнений мы устанавливаем такие зависимости между искомыми и данными величинами. Вначале вни­мательно изучается условие задачи, рассматривается смысл той или иной данной величины. Для более трудных задач используем иллюстрации в виде чертежа или схемы. Предполагая задачу решенной, мы некоторую величину обозначаем буквой х (или другой буквой) и считаем ее известной. Устанавливаем зависимости между этой величиной и величинами, данными в условии задачи, причем из многообразия различных зависимостей выби­раем те, которые позволят решить задачу, в данном случае составить уравнение.

Сделаем подобный анализ задачи на по­строение: «Построить треугольник, зная основание, меньший угол при основании и разность двух других сторон».

Чтобы найти решение, нужно вначале изучить усло­вие задачи, посмотреть, какие элементы искомого тре­угольники даны. Для этого начертим произвольный тре­угольник А₁В₁С₁ (рис. 25) иотметим элементы, соответ­ствующие данным по усло­вию. Пусть это будет сторо­на А₁С₁ и угол С₁А₁В₁. Но на чертеже нет разности двух других сторон. А так как для решения задачи мы должны учесть все данные, то нуж­но показать и разность.

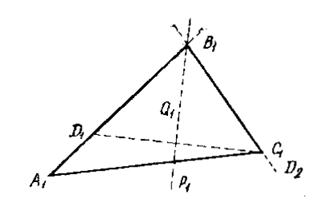
Рис. 25

Это можно сделать четырьмя способами: на меньшей стороне отложить большую от точки С₁ или от точки В₁ либо на большей отложить меньшую и вновь отклады­вать как от точки В₁, так и от точки А₁. Если разность будет около точки В₁, то тогда данные не связаны между собой и нельзя наметить план решения. Если же В₁ А₁ отложим от точки В₁ на В₁С₁, то данные: основание, угол при основании и разность двух других сторон – будут связаны между собой, но и эта связь не дает возможно­сти наметить план решения, она недостаточно жестка, чтобы построить, восстановить фигуру Д₂C₁A₁B₁. Лучше всего ввести разность, откладывая B₁D₁ = B₁C₁, так как в этом случае мы уже сможем восстановить фигуру С₁А₁Д₁. Конкретизировав таким образом данные задачи, приступаем к составлению плана решения.

Построив в произвольной прямой отрезок, равный основанию, получим две вершины треугольника: А₁ и С₁. Зная угол С₁А₁В₁, мы можем найти и положение точки D₁, где D₁А₁ = В₁А₁ – В₁С₁. Остается рассмотреть, как построить точку В₁ зная положение точки D₁. Так как С₁В₁ = В₁D₁, то точка В₁ равноудалена от точек С₁ и D₁,  поэтому она должна лежать на перпендикуляре Р₁Q₁, проведенном к отрезку С₁D₁ через его середину. Точка пересечения прямой Р₁Q₁ и луча А₁D₁ и будет точкой В₁. Следовательно, приходим к следующему построению. На произвольной прямой откладываем отрезок, равный основанию, и строим угол, равный данному, одна из сторон которого содержит построенный отрезок, а вер­шина совпадает с концом этого отрезка. На второй сто­роне угла откладываем отрезок, равный разности двух других сторон треугольника, и строим геометрическое место точек, равноудаленных от соответствующих кон­цов основания и построенного отрезка. Точку пересече­ния этого геометрического места со стороной угла, содержащей разность, соединяем с концом основании и получаем искомый треугольник.

Из этого примера видно, что при отыскании реше­ния задачи на построение, как и для арифметических задач, применяется аналитико-синтетический метод. Сле­дуя от вопроса задачи, учитываем, какие элементы нам известны, и, наоборот, исходные данные комбинируем так, чтобы построить искомую фигуру. Название этапа анализ не означает, что для отыскания решения при­меняется только аналитический метод, подобно тому как и при доказательстве, которое иногда называют синтезом, не всегда применяется синтетический метод рассуждения. При разборе задачи, при отыскании путей ее решения анализ и синтез находятся в постоянном взаимодействии, дополняют и проверяют друг друга.

Анализ задачи связан с исходным чертежом, по­этому его необходимо выполнять аккуратно, а фигура должна иметь наиболее общую форму. Если речь идет о треугольнике, то нужно брать разносторонний тре­угольник; о трапеции, то не равнобочную трапецию; если о четырехугольнике вообще, то и чертим четырехуголь­ник, который не был бы ни параллелограммом, ни трапе­цией. Если, например, решая задачу на построение тре­угольника, выберем для анализа равносторонний тре­угольник, то учащиеся вместо нужных зависимостей между данными и искомыми элементами могут исполь­зовать и другие связи, которые возникнут у них под впе­чатлением равносторонности треугольника.

Чертеж необходимо выполнять аккуратно чертежны­ми инструментами, и лишь после приобретения навыков в вычерчивании отрезков без линейки можно выполнять его от руки. Навыки выполнения чертежей или рисунков от руки особенно необходимы для учащихся, которые в будущем будут иметь дело с техникой, где они должны уметь делать эскизы деталей. С этим они не смогут спра­виться, не имея простейших навыков технического рисо­вания и черчения.

Чертеж должен строго соответствовать условию зада­чи. В ряде случаев целесообразно при анализе построе­ние чертежа начинать не с данных, а с искомых элемен­тов фигуры. Если, например, искомая окружность по условию касается некоторой прямой и некоторой окруж­ности в данной на ней точке, то и на чертеже для анализа мы должны видеть их касающимися. Следовательно, вначале надо построить окружность, изображающую искомую, и пристроить касающиеся ее произвольные прямую и окружность.

Таким образом, для отыскания решения задач на построение первое время необходимо использовать на­выки, приобретенные учащимися при решении арифме­тических задач, а затем уже и навыки, приобретенные при решении основных задач на построение и других математических задач. Используем также теоретический материал, в том числе и специальные методы геометри­ческих построений.

Построение.

1. Второй этап решения задач на построение состоит из двух частей: 1) перечисление в определенном порядке всех элементарных построений, которые нужно выпол­нить, согласно анализу, для решения задачи; 2) непо­средственное выполнение этих построений на чертеже при помощи чертежных инструментов. Действительно, решить задачу с помощью тех или иных инструментов – значит указать конечную совокупность элементарных, допустимых для данных инструментов, построений, вы­полнение которых в определенной последовательности позволяет дать ответ на вопрос задачи. Например, до­пустимыми построениями, которые определяют понятие «с помощью циркуля и линейки», являются следующие: 1) построение прямой, проходящей через две данные точки; 2) построение точки пересечения двух данных прямых; 3) построение окружности данного радиуса при заданном центре; 4) построение точек пересечения двух данных окружностей; 5) построение точек пересечении данной прямой и данной окружности.

Уже при решении простейших задач мы встречаемся с такими случаями, когда последовательность элемен­тарных построений, нужных для построения искомой фигуры, указана, а практически осуществить их нельзя. Например, требуется построить треугольник по трем сторонам. Всегда можно указать последовательность построений для решения этой задачи, но если одна из сторон больше суммы двух других, то треугольника не получим. И в стереометрии при решении конструктивных задач мы не всегда можем, например, выполнить постро­ение плоскости или сферы так, как мы строим на пло­скости прямые и окружности. И тогда главным является уже не фактическое построение, а указание, в какой последовательности нужно выполнять определенные построения, чтобы решить задачу. Например: «Через дан­ную точку А провести прямую, параллельную данной прямой МN, не. проходящей через точку А». Для этого через точку А и прямую МN проводим плоскость и в ней через точку А проводим прямую, параллельную прямой МN. Задача считается решенной, хоти эти построения мы выполнить не можем.

2. Перечисление элементарных построений в разделе «Построение» не всегда является повторением анализа. При анализе мы находим лишь план решения (как и при решении арифметических задач), а потом уже осущест­вляем его, записывая в форме вопросов с выполненными соответствующими действиями; недостаточно лишь уста­новить, как мы будем решать задачу, а нужно привести и само решение.

И при решении конструктивных задач, наметив план построении, нужно еще указать, как оно выполняется, так как нередко одно и то же построение, указанное в ана­лизе, можно осуществить различными способами.

Решение одной и той же задачи несколькими спосо­бами усиливает интерес учащихся к задачам на построе­ние и сознательное отношение к решению таких задач. Если решать задачи на построение все время по заранее указанным методам, то этим самым сковывается изобретательность и инициатива учащихся в нахождении раз­личных и оригинальных способов решения и им трудно научиться самостоятельно решать конструктивные за­дачи. Они применяют в первую очередь знания изучае­мого материала и навыки, полученные при решении задач, предшествующих данной. Если решались задачи, требующие применения определенного метода, то и для предложенной задачи они изобретут тот же знакомый им путь решения, даже если он нерационален. Указание учителя на существование более простого способа не дает должного эффекта, так как предложенное учителем ре­шение кажется учащимся искусственным, которого они сами не смогли бы найти.

Конечно, если это делать до того как ученики при­обретут прочные навыки в отыскании решений различ­ными способами, то результаты окажутся отрицатель­ными. Внимание учащихся каждый раз будет распылять­ся между всеми способами, и они ни одного из них не усвоят основательно, чтобы применять его достаточно сознательно.

Различными способами хорошо решать задачи в конце учебного года, при повторении курса геометрии, когда учащиеся уже имеют достаточные навыки в решении задач на построение. Задачу, допускающую различные способы решения, лучше задавать на дом, чтобы они не только решили, но и нашли наиболее простое решение.

Сам учитель должен выбирать тот способ решения, который является наилучшим и с теоретической и с мето­дической точек зрения. Нельзя руководствоваться только простотой построения, понятием геометрографии. Следует учитывать не только трудность выполнения построе­ния, но и трудности анализа, доказательства и исследо­вания.

3. Из приведенных примеров видно, что решение не всегда сводится к элементарным построениям, а чаще всего к так называемым основным построениям или основным задачам на построение. Подобно тому, как при доказательстве теорем используются и результаты ранее изученных теорем, а не только аксиом, так и при решении задач на построение при анализе и описании построения используются ранее решенные задачи. Задачи, решение которых в дальнейшем часто используется, обычно отно­сят к основным задачам на построение. Список основных задач на построение определяется учебником, но надо помнить, что задача на построение может или не может быть отнесена к основным и в зависимости от степени подготовки учащихся.

В средней школе нецелесообразно при решении каждой задачи требовать от учащихся в письменной или устной форме подробного описания построений. Такое описание, особенно в VI-VII классах, требует большой затраты времени. Интерес учащихся к решению задач на построение понижается, ибо главной трудностью стано­вится изложение решения, сводящееся иногда к целым «сочинениям».

Если анализ задачи выполнен достаточно подробно, то и при устном пояснении к решению, и в письменных работах достаточно, если ученик указывает, например: «Строим прямоугольный треугольник по гипотенузе и ка­тету», – и верно выполняет это построение. Учитель все­гда в состоянии проверить, правильно ли выполнил ученик построение, если даже описание и отсутствует. Нередко, разобрав с учащимися условие задачи и на­метив план построения, предлагаем учащимся выполнить это построение в тетрадях, не требуя каких-либо поясне­ний в письменной форме.

Важна и цель, для достижения которой решается та или иная задача на построение. Если на данном уроке, например, главная цель решения задач – обучение отыс­канию решений, то мы стремимся научить учащихся анализировать условие задачи, уметь видеть на чертеже нужные фигуры и имеющиеся отношения между фигура­ми и их элементами. В таком случае незачем усложнять работу требованием подробного описания построения. Все внимание учащихся должно быть сосредоточено на главном, и не нужно распылять его на второстепенные вопросы, не имеющие прямого отношения к поставленной цели.

Если на первых порах решения задач на построение мы всегда требуем непосредственного выполнения по­строения инструментами, то нередко, когда убеждены, что все учащиеся класса сумеют выполнить чертеж с по­мощью инструментов, разрешаем учащимся указывать лишь план построении, выполняя чертеж от руки, а ино­гда просто ограничиваемся лишь составлением плана построения, то есть анализом, или с проведением еще исследования.

4. С введением геометрического материала в курс арифметики учащиеся уже в V классе приобретают навыки в применении таких инструментов, как линейка, циркуль, чертежный треугольник, знакомятся с устройством и применением транспортира. При вычерчивании секторных диаграмм, а также на уроках географии они закрепляют свои знания об устройстве транспортира и приобретают навыки в применении его для измерения углов и для построения заданных углов. На уроках труда в школьных мастерских пятиклассники при разметке при­меняют линейку, циркуль, угольник. Эти навыки закреп­ляются в VI классе при изучении первой темы курса геометрии «Основные понятия».

При изучении свойств прямой учащиеся выполняют построения всевозможных прямых через одну, две, три, четыре точки. Выполняя необходимые построения, они убеждаются, что через одну точку можно провести сколь­ко угодно прямых, через две – только одну, через три точки можно провести три прямые или только одну, четы­ре точки могут определять только одну прямую, или четыре прямые, или шесть прямых. Это содействует раз­витию пространственных представлений.

Учащиеся должны приобрести прочные навыки в вы­полнении действий над отрезками и в выполнении нало­жения одного отрезка на другой, что существенно важно для дальнейшей работы. Здесь они закрепляют навыки в применении линейки и циркуля, так как часто нужно уметь «взять» отрезок циркулем, отложить его на произ­вольной прямой, сравнить отрезки путем наложения одного на другой. Применение транспортира, причем не только в качестве малки, но и для измерения углов, облегчает усвоение раздела «Сравнение углов. Действия над углами: сложение, вычитание, умножение на целое число. Биссектриса угла».

Доказательство.

1. После того как фигура построена, необходимо установить, удовлетворяет ли она условиям задачи, то есть показать, что фигура, полученная из данных элемен­тов определенным построением, удовлетворяет всем усло­виям задачи. Значит, доказательство существенно за­висит от способа построения. Одну и ту же задачу можно решать различными способами, в зависимости от наме­ченного при анализе пла­на построения, а поэтому, и доказательство в каж­дом случае будет свое, Рассмотрим задачу: «По­строить трапецию по четы­рем сторонам» (рис. 26).

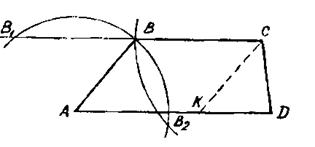 Рис. 26

Проведя СК||ВА, решение задачи сводим к построению треугольника КСD по трем сторонам: две равны боковым сторонам трапеции (АК = КС), а КD = АD – ВС. Построим треугольник КСD, и, считая сторону АD построенной, допол­ним его до трапеции различными способами:

1) Проведем ВС||АD и, отложив меньшее основание, соединим полученную точку В с А Доказательство све­дется к установлению равенства: АВ = КС.

2) Если провести АВ||КС и ВС||АD, то тогда уже надо доказать, что АВ = КС и ВС = АК.

3) Если провести прямую СВ||DА и на ней найти точки В и В₁, отстоящие от А на расстоянии, равном бо­ковой стороне, то в этом случае точка В₁ будет посторон­ней и лишь точка В будет искомой, причем доказатель­ство (ВС = АК) уже усложняется.

4) Если отыскивать точку В, как точку пересечения окружностей (А; АВ) и (С; СВ), то из двух точек В и В₂ только точка В будет искомой.

Третий и четвертый случаи подчеркивают необходи­мость доказательства. В анализе мы находим необходи­мые условия, которым должно подчиняться построение, чтобы получить искомую фигуру. Надо еще установить, что найденные необходимые условия являются и доста­точными, то есть, что построенная фигура удовлетворяет всем требованиям задачи.

2. При решении простейших задач, когда все условия задачи находят непосредственное отражение в плане по­строения, нет необходимости доказывать, что фигура, полученная из данных элементов таким построением, является искомой. Например: «Построить треугольник по двум сторонам и углу между ними». Здесь доказатель­ство сводится к простой проверке, такие ли взяли сторо­ны, как данные, и будет ли построенный угол равен дан­ному. В подобных задачах доказательство является излишним, ибо правильность решения обеспечивается соответствием построения анализу и данным условия задачи.

Но иногда не все условия отражаются в плане анали­за и при построении. Например, в случае (3) точка В действительно должна лежать на ВС и отстоять от точки А на данном расстоянии. Но этого недостаточно, так как отрезок АВ должен быть параллельным СК.

Так как доказательство зависит от избранного реше­ния, то, не ознакомившись с анализом и построением, нельзя сказать, правильно пли неправильно проведено доказательство.

3. Доказательство не просто зависит от анализа и по­строения, между ними существует взаимосвязь и взаимообусловленность. Построение проводится по пла­ну, составленному при анализе. Таких планов можно указать несколько. Построение и доказательство являют­ся своеобразным критерием правильности и рациональности составленного плана. Если план не осуществим имеющимися инструментами или же построение оказыва­ется нерациональным, мы вынуждены искать новый план решения. Аналогичным образом и доказательство, и исследование влияют на анализ, предопределяя нередко выбор плана решения.

4. Для упрощения доказательства целесообразно предлагать учащимся и такие задачи на доказательство, которые не только служат для развития математического мышления или для пополнения объема знаний, но и могут быть использованы при решении задач на построение. Например, при изучении частных видов параллелограм­ма решаем задачи:

1) Если у параллелограмма диагонали взаимно пер­пендикулярны, то такой параллелограмм есть ромб.

2) Если у параллелограмма диагональ делит один из углов пополам, то такой параллелограмм есть ромб.

3) Если у параллелограмма диагонали равны, то та­кой параллелограмм есть прямоугольник и т. п.

При решении задач на построение методом подобия, выбрав центр подобия и найдя коэффициент подобия, выполняем подобное преобразование многоугольника, подобного искомому, почти всегда не тем способом, который изложен в учебнике А. П. Киселева, и всякий раз вынуждены проводить отдельное доказательство, что по­лученный многоугольник – искомый. Целесообразно ознакомить учащихся с общепринятым способом по­строении, основанным на том, что у гомотетичных многоугольников сходственные стороны попарно параллельны. Благодаря этому при решении почти всех задач на по­строение многоугольников методом подобия доказательство, что полученный многоугольник искомый, значи­тельно упрощается.

5. Хотя доказательство при решении задач на построение проводится аналогично доказательству теорем, с использованием аксиом, теорем и свойств геометрических фигур, между ними имеется и некоторое раз­личие. При доказательстве теорем в большинстве случа­ев без труда выделяют условие и заключение. При ре­шении задач на построение уже труднее найти данные, на основании которых можно доказать, что построенная фигура является искомой. Поэтому при решении кон­структивных задач в классе целесообразно иногда спе­циально выделять, что дано и что требуется доказать. Например, при решении задачи: «Построить ромб по двум его диагоналям» предлагаем ученику записать, что дано (диагонали взаимно перпендикулярны и, пересекаясь, делятся пополам) и что требуется доказать (стороны равны). Однако при решении задач дома и в кон­трольных работах мы не требуем оформления доказа­тельства с выделением отдельно условия и заключения.

Нет надобности требовать проведения особого дока­зательства в задачах, где правильность решении очевид­на. А иногда, если даже правильность решении и не усматривается непосредственно, учитель, учитывая на­значение решаемых задач, может не требовать доказательства, предупредив об этом учащихся.

Исследование.

Сущность и значение исследования.

Каждая задача на построение включает в себя требование построить геометрическую фигуру, удовле­творяющую определенным условиям, которые в боль­шинстве своем задаются размерами или положенном некоторых геометрических образов. Условия задач фор­мулируются в самом общем виде, а поэтому исходные данные являются как бы параметрами, принимающими всевозможные допустимые значения.

Допустимые значения определяются наиболее есте­ственным образом. В задаче: «Построить треугольник по двум сторонам а и b и углу С между ними» допусти­мыми значениями для а и b будут всевозможные отрез­ки, которые можно характеризовать положительными числами, их длинами, а угол С может принимать все­возможные значения от 0° до 180°.

В задаче: «Построить окружность, касающуюся длиной окружности в данной на ней точке и данной прямой» прямая может занимать любое положение на плоскости; окружностью также может быть любая окружность на плоскости, но так как окружность характери­зуется положением центра и величиной радиуса, то мож­но сказать, что центром данной окружности может быть любая точка плоскости, а радиусом – любой отрезок, длина которого 0 < R < ∞. (Иногда рассматривают и направленные окружности, тогда уже радиус может быть и неположительным чистом, но подобные случаи обычно оговариваются в условии задачи.) Точка также может занимать произвольное положение, но уже не на плос­кости, а на данной окружности, так как она обязательно должна принадлежать ей.

Иногда невозможность построения искомой фигу­ры очевидна, если хоть один из данных элементов не принадлежит области допустимых значений. Например: «Построить треугольник по двум сторонам а и b и углу между ними в 240°». Такая задача решения не имеет, так как любой угол треугольника всегда меньше 180°.

Но если все данные принадлежат соответствующей области существования, то в большинстве случаев много­образие возможных положений, характер изменения данных приводит, как и в алгебре при решении задач с параметрическими данными, к постановке вопросов: При каких данных задача не имеет решения? Как изме­няется ответ при определенном характере изменения дан­ных? Каковы должны быть значения исходных данных, чтобы получить намеченный ответ? и т. п.

При анализе, а значит, и при построении всегда исходим из предположения, что искомая фигура сущест­вует, не учитывая всего многообразия данных, их разме­ров и взаимных соотношений. Решение задачи на построение считается законченным, если указаны необхо­димые и достаточные условия, при которых найденное решение является ответом на задачу. Значит, мы долж­ны установить, при всяком ли выборе данных задача имеет решение и если имеет, то сколько. Например: «Построить окружность, проходящую через три данные раз­личные точки». Если данные точки не лежат на одной прямой, то задача имеет решение и притом только одно; если же точки лежат на одной прямой, то задача реше­ния не имеет.

Если при определенном сочетании данных общее ре­шение не применимо, то необходимо дать новое решение, которое часто не незначительно отличается от общего или является его вырожденным случаем. Иногда план реше­ния сохраняется, по его осу­ществление с помощью ин­струментов выполняется не так, как в общем случае.

В средней школе обычно ограничиваются лишь двумя моментами: 1) выясняют число решений в зависимости от данных и 2) изменяют или упрощают решение для отдельных случаев. Правда, для некоторых задач в исследовании дается еще и ответ па вопрос: при каких условиях искомая фигура удовлетворяет тем или иным дополнительным условиям. Например: «Около данного треугольника описать окружность. Выяснить, когда центр этой окружности находится внутри треугольника, вне треугольника или принадлежит одной из его сторон». Ответ на последний вопрос также дается при исследовании.

Исследование является составной частью реше­ния. Решение задачи на построение можно считать за­конченным, если узнаем, сколько искомых фигур полу­чим при определенных данных, и, в частности, указано, когда не получим искомый геометрический образ. Но ис­следование в задачах на построение, как и исследование при решении других задач по математике, имеет и общеобразовательное значение.

В процессе исследования учащиеся упражняются в практическом применении диалектического метода мы­шления. Они видят, что изменение данных задачи вызы­вает изменение искомой фигуры. Мы имеем дело не с за­костенелыми, а с изменяющимися геометрическими образами, изменение одних величин обусловлено изменением других.

Для правильного проведения исследования нужно обладать хорошо развитым логическим мышлением. Значит, с другой стороны, исследование задач на по­строение является хорошим материалом для развития логического мышления учащихся.

Заметим, что и при решении задач на доказательст­во или вычисление учащимся нередко нужно для по­строения правильного чертежа также проводить иссле­дование. Часто необходимо предварительно выяснить, какой вид данного треугольника (остроугольный или ту­поугольный), какие стороны принять равными данным отрезкам. Например, при решении задачи: «Определить периметр равнобедренного треугольника со сторонами в 7 см и 3 см» вначале нужно установить, что основанием является отрезок длиной 3 см, а не 7 см.

Нередко уже при анализе задач на построение мы вынуждены учитывать различные положения данных и искомых элементов. Например, решая задачу: «Дана окружность и на ней три точки М, N и Р, в которых пере­секаются с окружностью (при продолжении) высота, биссектриса и медиана, исходящие из одной вершины вписанного треугольника. Построить этот треугольник», в первую очередь нужно выяснить, что точка N (соответ­ствует биссектрисе) расположена между М и Р, рассмат­ривая дугу MP, меньшую полуокружности.

Приведем еще такой пример: «На окружности даны две точки А и В. Из этих точек провести две параллель­ные хорды, сумма которых дана». Решение задачи легко свести к построению вписанной трапеции с заданной сум­мой оснований, вершинами которой являются точки А и В. Но решение зависит от того, будет ли АВ боковой сто­роной трапеции или ее диагональю. Вновь анализ вклю­чает в себя элементы исследования.

Несмотря на необходимость и целесообразность исследования при решении задач на построение, ему и в школе, и в методической литературе уделяется недоста­точно внимания. Большое внимание уделяется обычно отысканию решения – анализу. Анализ – основной этап при решении задач на построение: не найдя реше­ния, нельзя провести ни построения, ни доказательства, ни исследования. Но по трудности выполнения исследование является не менее сложным этапом. Наи­большее количество ошибок допускается именно при исследовании.

 

2.2.7. Методы решения задач на построение.

Метод геометрических мест.

1. Понятие «геометрическое место точек», являющее­ся синонимом понятия «множество», одного из основных понятий современной математики, вводится в элементар­ной геометрии исключительно ввиду его наглядности, образности; слово «место» как бы отвечает на вопрос, где «помещаются» точки, обладающие тем или иным свойством.

Знание геометрических мест точек, обладающих определенным свойством, облегчает нахождение реше­ния для многих практических задач. Например, для ре­шения задач на сопряжение окружностей и прямых, с ко­торыми учащиеся встречаются довольно часто на уро­ках труда в школьных мастерских при опиливании криволинейных поверхностей (изготовление дуги для лобзика, отвертки, гаечного ключа и т. п.), при изготов­лении приборов, пособий для школы, которые они часто делают не по чертежам, а по техническим рисункам, не выполняя деталировки каждой детали, необходимо знать соответствующие геометрические места. Без знания геометрических мест центров окружностей, касающихся данных прямых или окружностей при определенных ограничениях, семиклассники не смогут на уроках чер­чения понять способы решения задач на сопряжение углов дугами, сопряжение окружности с прямой при помощи дуги данного радиуса и т.п.

Следует учитывать, что понятие «геометрическое ме­сто точек» необходимо и в курсе алгебры при изучении графиков простейших функций в VII-VIII классах. График функции определяется как геометрическое место точек плоскости, координаты которых являются соответственными значениями аргумента и функции. Понятие графика необходимо и в курсе физики, где в последние годы все большее значение приобретает графический метод.

В VI-VII классах нельзя отказываться и от решения задач на построение методом геометрических мест, од­ним из основных методов конструктивной геометрии.

Решая задачи на построение, учащиеся учатся при­менять свои знания, ибо они должны сами отвечать на поставленные вопросы. В настоящее время главной задачей учителей математики является не столько сообще­ние математических фактов, определений, формул, тео­рем, сколько необходимость учить детей мыслить, учить их самостоятельно работать.

2. Учащиеся VI класса не сразу сознательно, глубоко усвоят понятие «геометрическое место точек». Важно, чтобы они с данными словами связывали более полную группу геометрических фигур, чтобы понятие охваты­вало целый класс, а не один – два отдельных примера. Учащиеся должны видеть различные примеры геометри­ческих мест точек в различных формулировках, чтобы на основе анализа и синтеза осознать общность этого понятия, охватывающего обширный класс геометриче­ских фигур, создать себе соответствующее представление об этом понятии.

Трудным для понимания шестиклассников является и абстрактное понятие «множество». Приводимые при­меры множеств (множество учащихся, деревьев в саду и т.п.), в большинстве своем, есть конечные множества, а почти все геометрические места точек, рассматривае­мые в школьном курсе геометрии, являются бесконечны­ми точечными множествами.

3. Понятие геометрического места точек, обладаю­щих некоторым свойством, вводим на примере геометрического места точек, равноудаленных от двух данных точек. После изучения признаков равенства прямоуголь­ных треугольников решаем задачу: «Найти точку, рав­ноудаленную от двух данных точек А и В» (рис. 27).

Рис. 27

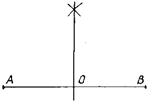Учащиеся обычно указывают лишь точку О, середину отрезка АВ. А нет ли на плоскости еще точек, равноуда­ленных от А и В? При построе­нии с помощью циркуля не- скольких таких точек учащиеся самостоятельно припоминают свойство точек оси симметрии и говорят, что точек, равноудаленных от А и В, будет много, все они лежат на оси симмет­рии данных точек А и В.

Можно непосредственно, основываясь на признаках ра­венства прямоугольных тре­угольников, доказать, что всякая точка, равноудаленная от данных точек А и В, лежит на их оси симметрии, то есть на перпендикуляре, проведенном к отрезку АВ через его середину, и наоборот, всякая точка этого перпендику­ляра равноудалена от точек А и В.

После этого даем определение геометрического места точек, обладающих некоторым свойством, как множест­ва всех точек, обладающих этим свойством, и только та­ких точек, и предлагаем учащимся сформулировать ре­зультат решения задачи и записать в тетради, что гео­метрическое место точек, равноудаленных от двух точек, есть ось симметрии данных точек.

Здесь впервые встречаемся не с отдельной, фиксиро­ванной точкой, а с любой точкой прямой. До этого уча­щиеся почти всегда имели дело с неподвижными, опре­деленными по положению точками, а здесь точка может перемещаться некоторым образом, но все время она об­ладает определенным свойством. Поэтому большую пользу окажет учащимся наглядное пособие с непо­движными точками А и В и перемещающейся по их оси симметрии точкой О, соединенной резинкой с точками А и В, с помощью которого хорошо разъяснить смысл выражения: «Любая точка оси симметрии равноудалена от А и В».

Примечание. Включение в определение лишних с научной точки зрения слов «и только таких точек» вызвано педагогическими соображениями. В противном случае в определении явно не выделяется необходимость доказательства двух взаимно обратных теорем для утверждения, что та или иная фигура является геометрическим местом точек, обладающих определенным свойством.

4. Целесообразно в качестве домашнего задания к этому уроку предложить учащимся повторить определе­ние окружности (§ 12 по учебнику Н. Н. Никитина). То­гда на уроке, уточнив, что все точки окружности нахо­дятся от центра на одном и том же расстоянии, а всякая точка, взятая внутри (вне) окружности, находится от ее центра на расстоянии, меньшем (большем) радиуса, делаем вывод, что окружность можно рассматривать как геометрическое место точек плоскости, находящихся на данном расстоянии R от данной точки О.

Предлагаем учащимся самостоятельно найти все точки, находящиеся от данной точки О на расстоянии, меньшем чем R. И при разборе этого задания подчерки­ваем, что геометрическим местом точек может быть пря­мая, окружность и даже круг, а в дальнейшем будет показано, что геометрическим местом точек, обладаю­щих некоторым свойством, может быть луч, отрезок прямой, две прямые или две окружности и даже отдельные точки. Разбирая такие конкретные примеры, мы пока­зываем учащимся разнообразие видов тех множеств то­чек, которые могут быть геометрическими местами точек.

Затем надо показать учащимся, что одно и то же гео­метрическое место точек может встречаться в различ­ных формулировках, для чего сравниваем, например, из­вестное им геометрическое место точек, равноудаленных от двух данных точек, с такими, как геометрическое место точек, равноудаленных от концов дачного отрезка; геометрическое место вершин равнобедренных треуголь­ников с общим основанием (середина основания уже исключается).

5. Применяя эти геометрические места точек, решаем задачи методом геометрических мест, начиная с простей­шей задачи. Какие же задачи считать простейшими?

Сущность метода геометрических мест состоит в сле­дующем:

1)  Решение задачи сводим к отысканию точки, удо­влетворяющей определенным условиям.

2) Отбрасываем одно из этих условий, получим гео­метрическое место точек, удовлетворяющих оставшимся условиям.

3) Отбрасываем затем какое-нибудь другое условие, получим новое геометрическое место точек, удовлетворяющих остальным условиям.

4) Искомая точка, удовлетворяющая всем условиям, является точкой пересечения полученных геометрических мест.

Какую задачу ни возьмем, одновременно второй и третий этапы отсутствовать не могут, ибо тогда это не была бы задача на метод геометрических мест. Но без одного из этих этапов можно обойтись, если в условии указать геометрическую фигуру, которой должна при­надлежать искомая точка. Чтобы избежать и первого этапа, достаточно задачу сформулировать в виде: «Най­ти точку...».

Следовательно, простейшими задачами на метод гео­метрических мест будут задачи вида: «На какой-либо фигуре найти точку, удовлетворяющую определенным условиям.

Метод осевой симметрии.