Навигация
Осевая симметрия – это первый из видов движения, преобразования, с которым учащиеся встречаются в систематическом курсе геометрии
1. Осевая симметрия – это первый из видов движения, преобразования, с которым учащиеся встречаются в систематическом курсе геометрии.
В настоящее время в геометрии большое значение имеют конструктивные навыки, при помощи которых учащиеся овладевают методами преобразования одних геометрических фигур в другие, и постепенно знакомятся с важной идеей геометрического преобразования, которое является аналогом функциональной зависимости в геометрии.
Курсы алгебры и арифметики подчинены одной идее, идее функциональной зависимости. Мы стремимся воспитывать у учащихся функциональное мышление, умение находить законы связей между величинами. Подчинив курс геометрии идее геометрических преобразований, аналогу функциональной зависимости, подчиняем все изложение курса математики одной руководящей идее.
В новой программе по геометрии значительное внимание уделено геометрическим преобразованиям, то есть таким операциям, когда каждой точке одной фигуры по некоторому закону ставится в соответствие определенная точка другой фигуры. В средней школе из геометрических преобразований рассматриваются различные виды движений, а также подобие фигур.
Изучение движения в средней школе принесет ощутимые плоды, если эти преобразования станут основой курса геометрии, а не придатком, органически не связанным с ним. Движение должно служить одним из основных методов доказательства многих теорем геометрии в VI-VII классах. Более того, идея движения может быть положена в основу построения значительной части курса геометрии. Излагаемый материал приобретает кинематический характер, значительно облегчается понимание учащимися образования и построения геометрических фигур. Применяя понятие осевой симметрии, можно значительно усовершенствовать школьный курс геометрии. Например, применение свойств оси симметрии позволяет довольно просто изложить три признака равенства треугольников, специальные случаи равенства прямоугольных треугольников и ряд других тем из главы «Треугольники».
2. Различные виды движений дают возможность решать практически важные задачи на построение, доказательство и задачи вычислительного характера. Поэтому все изложение должно сопровождаться упражнениями, среди которых предпочтение следует отдавать задачам на построение и на доказательство. Нужно решать и задачи на вычисление, особенно с практическим содержанием, но в большинстве случаев при решении таких задач геометрическая сторона вопроса в значительной степени поглощается арифметическими и алгебраическими операциями.
3. Известно, что осознанные знания могут быть получены только в процессе активной и творческой деятельности самостоятельно или под руководством учителя. При изучении осевой симметрии имеются большие возможности привлечь учащихся к формированию самого понятия. Действительно, учащиеся неоднократно наблюдали в жизни примеры симметричных фигур, многие из таких предметов они рисовали или изготовляли на уроках в начальной школе и в V классе: вырезали симметричные фигуры из бумаги, рисовали симметричные орнаменты, листья и цветы, изготовляли симметричные предметы из дерева и металла, применяя симметричные инструменты.
Анализируя эти знакомые учащимся примеры, особенно примеры предметов, которые были объектом или орудием трудa учащихся в школьных мастерских, на уроках домоводства или общественно полезного труда, мы постепенно формируем представление о симметричных фигурах.
Часть работ (изготовление мотыги, планки для граблей и т. п.), требующих построения точек, симметричных относительно определенной оси, учащиеся изготавливают до изучения соответствующего материала в курсе геометрии. поэтому при объяснении осевой симметрии, чтобы подчеркнуть значение этого понятия, в качестве симметричных фигур использовали пособия, изготовленные учащимися этого же класса в школьных мастерских, причем выбирали всегда два однотипных пособия 9молотки, стамески), одно из которых сделано аккуратно, точно по чертежу, а второе такое, у которого все размеры выдержаны, но нарушена симметричность. Совместными усилиями учащиеся выяснили, почему второе пособие получилось плохим, и как нужно было правильно сделать разметку.
4. В школьном курсе геометрии выражение «симметрия» имеет двоякий смысл: оно обозначает и вид движения (преобразование) и свойство плоской фигуры, обладающей симметрией, которая при соответствующем движении переходит сама в себя. Это различие мы должны учитывать, ибо в преподавании приходится иметь дело с каждым из этих истолкований симметрии. И одна из задач учителя – добиться того, чтобы учащиеся восприняли симметрию как один из способов преобразования одной фигуры в другую, а не как свойство неподвижной фигуры.
Поэтому после введения определения симметричных относительно оси точек, внимание учащихся переключаем на практику построения взаимно симметричных относительно оси фигур, для чего решаем задачи вида:
1) Построить точку, симметричную данной точке относительно данной прямой.
2) Построить отрезок (прямую), симметричный данному отрезку (прямой) относительно данной прямой.
3) Построить треугольник, симметричный данному треугольнику относительно данной прямой.
4) Построить окружность, симметричную данной окружности относительно данной прямой.
5) Построить треугольник, симметричный данному прямоугольному треугольнику относительно а) его катета; б) его гипотенузы.
При решении этих задач одновременно устанавливаем и равенство взаимно симметричных отрезков, углов и других фигур, иллюстрируя наши утверждения перегибанием чертежа по оси симметрии, что помогает найти и сделать понятным способ решения задачи. Например, при решении задач вида: «Даны две прямые. Найти на них точки, симметричные относительно третьей прямой» очень удобно нанести все три прямые на кальку и перегнуть чертеж по третьей прямой. Тогда решение задачи становится очевидным и понятным для всех учащихся. Таким же образом решаем задачи: а) Даны прямая и треугольник. Найти на одной прямой и на контуре треугольника точки, симметричные друг другу относительно другой прямой, б) Даны окружность и треугольник. Найти на окружности и на контуре треугольника точки, симметричные друг другу относительно данной прямой.
Чтобы показать учащимся важность и необходимость умений и навыков в построении симметричных относительно оси точек, кроме разбора известных уже им примеров, полезно выполнить разметку какого-нибудь изделия, которое нужно будет изготовлять в ближайшее гремя.
5. Обучение должно вестись так, чтобы учащиеся усвоили знания не как изолированные, оторванные от других, а как подготовленные предшествующими знаниями, и которые естественно включаются в последующие. Поэтому в дальнейшем, где только возможно, следует использовать понятие и свойства осевой симметрии и правила построения симметричных фигур при изучении новых геометрических образов и при решении доступных учащимся задач на построение.
Знание свойств симметричных относительно оси фигур позволяет рассматривать решение основных задач на построение с помощью циркуля и линейки до изучения признаков равенства треугольников и понятия геометрического места точек. Сами построения являются для учащихся понятными и естественными.
Действительно, чтобы построить точку, симметричную относительно некоторой прямой данной точке А, не лежащей на этой прямой, построим две окружности, проходящие через точку А с центрами в произвольных точках О1, и О2 данной прямой. Так как для окружностей данная прямая является осью симметрии, то вторая их общая точка А1 будет искомой точкой. Но этим самым мы решили и задачу: «Через точку А, не лежащую на данной прямой, пронести перпендикуляр к этой прямой,
Аналогичным образом решается и задача о построении оси симметрии двух данных точек; одновременно получаем решение задачи о делении данного отрезка пополам.
Так как биссектриса угла есть ось симметрии его сторон, то для построения ее достаточно найти на сторонах угла две точки, симметричные относительно искомой оси, каковыми будут точки, находящиеся на равных расстояниях от вершины угла, принадлежащей оси симметрии. В результате задача свелась к предыдущей с той лишь разницей, что достаточно найти одну точку оси, так как вторая точка – вершина угла – нам известна.
Этим же построением решается и задача о проведении к прямой перпендикуляра через данную на ней точку, так как искомый перпендикуляр по существу есть биссектриса развернутого угла с вершиной в данной точке.
Применение осевой симметрии значительно упрощает и облегчает усвоение таких разделов темы «Окружность», как свойство диаметра, перпендикулярного к хорде, свойство дуг, заключенных между параллельными хордами. Без большой затраты времени можно тщательно рассмотреть весьма важный для приложений вопрос о взаимном расположении окружностей, если обратить внимание учащихся на симметричность общих точек двух окружностей относительно их линии центров. Учащиеся смогут самостоятельно указать необходимые и достаточные условия касания двух окружностей, что нужно при изучении соответствующих геометрических мест центров окружностей, касающихся данной.
В VII-VIII классах метод осевой симметрии часто применяется вместе с другими методами.
Метод центральной симметрии.
1. В течение двух лет мы знакомили учащихся с центральной симметрией примерно так, как в учебнике Н.Н. Никитина. Рассматривали построение и свойства точек, отрезков и треугольников, симметричных соответствующим данным фигурам относительно некоторой точки О. Затем рассматривали вопрос о центре симметрии параллелограмма, решая предварительно задачу: «Если в параллелограмме через точку О пересечения его диагоналей провести произвольную прямую, то отрезок прямой, заключенный между его сторонами, делится в точке О пополам». Получив соответствующий вывод о центре симметрии параллелограмма, вводим понятие центрально-симметричных фигур, подчеркивая, что каждой точке М фигуры, имеющей центр симметрии в точке О, соответствует другая точка М1 этой же фигуры, отстоящая от О на такое же расстояние, как и точка М, и лежащая на прямой МО.
Решали такие задачи на построение с применением центральной симметрии;
1) Построить треугольник по двум сторонам и медиане, проведенной к третьей стороне.
2) Дан угол и точка Р внутри него. Провести через эту точку прямую так, чтобы отрезок ее, заключенный между сторонами угла, делился в данной точке пополам.
У большинства учащихся не создавалось правильного представления о применении здесь центральной симметрии, они рассматривали эти решения, как решения задач дополнением искомых треугольников до параллелограммов.
Причины того, что это понятие оказалось трудным при таком изложении, следующие: во-первых, понятие центральной симметрии точек и фигур вводилось формально, без активного участия учащихся в формировании этого понятия; во-вторых, примеры задач на построение для иллюстрации применения центральной симметрии подобраны неудачно; в-третьих, в курсе геометрии по установившейся традиции центральная симметрия не находит должного применения.
2. Результаты оказались значительно лучшими, когда понятие центральной симметрии начали вводить так же, как и понятие осевой симметрии. Объяснение этого понятия сопровождалось показом соответствующих наглядных пособий, а также изделий, для которых учащиеся данного класса выполняли разметку, принимая точку пересечения базисных линий за центр симметрии и откладывая на одной и той же прямой по разные от этой точки стороны равные отрезки.
Затем решаем задачи вида: «Построить точку (отрезок, треугольник), симметричную данной точке (отрезку, треугольнику) относительно данного центра О», устанавливая одновременно равенство центрально-симметричных отрезков и треугольников. Чтобы учащиеся поняли, что любые центрально-симметричные фигуры равны, предлагаем им начертить произвольную прямолинейную фигуру и найти центрально-симметричную ей фигуру по отношению к некоторому центру. Поворачивая одну из них на 180о около центра О, учащиеся убеждаются, что эти фигуры совпадают. Затем, как и в прежнем варианте, вводим понятие центрально-симметричных фигур, рассматривая предварительно симметрию параллелограмма. Чтобы показать приложение центральной симметрии к решению задач на построение, подбираем задачи, для решения которых требуется применить действительно центральную симметрию, а не дополнение до параллелограмма.
Метод параллельного переноса.
В средней школе умножение движений не рассматривается, и мы не можем вводить параллельный перенос как произведение двух отражений около параллельных осей, а вынуждены исходить из свойств параллелограммов.
Целесообразно с параллельным переносом знакомить учащихся в процессе решения задач па построение при изучении темы «Четырехугольники».
Имеются задачи вычислительного характера и на доказательство, требующие проведения прямых, параллельных боковой стороне трапеции, или в которых уже проведена такая прямая, например:
1) В трапеции ABCD из вершины В проведена прямая, параллельная боковой стороне CD, до встречи в точке Е с большим основанием АD. Периметр треугольника АВЕ равен 1м, а длима ED равна 3дм. Определить периметр трапеции.
2) Доказать, что в равнобедренной трапеции углы при основании равны. Для решения этой задачи учащиеся проводят прямую, параллельную боковой стороне, чтобы свести доказываемое предложение к свойству равнобедренного треугольника.
Но перенос части фигуры, искусственно отделенной от других элементов, для учащихся более сложен, чем перенос всей фигуры. Поэтому можно было бы начинать с решения задачи, требующей переноса окружности. В этих задачах очень простое построение, так как фактически нужно перемещать в заданном направлении на данное расстояние лишь одну точку – центр окружности. Но при таком решении учащиеся не видят, как перемещаются точки окружности, ибо допустимо вращение окружности около центра, а это может привести к неправильному пониманию параллельного переноса. Например, в известном пособии И. И. Александрова первым примером на метол параллельного переноса является задача: «Между двумя окружностями провести отрезок ХУ, делящимся пополам в данной точке А». Приведенное там решение показывает, что вместо параллельного переноса окружности фактически выполнено отражение от точки А, которое можно в данном случае рассматривать как произведение параллельного переноса и поворота окружности вокруг своего центра на 180°.
Таким образом, при решении задач па построение мы применяем метод параллельного переноса, сущность которого состоит в следующем: при анализе какую-нибудь фигуру подвергаем параллельному переносу на некоторое расстояние в определенном направлении, в результате чего получаем вспомогательную фигуру, построение которой или очевидно, или не представляет затруднений. После этого производим обратный перенос и получаем искомую фигуру. Здесь же разъясняем, что параллельный перенос фигуры на некоторое расстояние означает, что все ее точки смещаются на одинаковое расстояние в определенном направлении. Следовательно, для определения параллельного переноса нужно знать направление и величину переноса.
Параллельным перенос можно задать вектором переноса, которым одновременно определял бы и направление и интервал данного переноса, но понятие вектора для семиклассников неизвестно, поэтому мы вынуждены выделять отдельно направление и величину переноса. В дальнейшем при решении всех задач па построение методом параллельного переноса требуем от учащихся указывать как направление переноса, так и расстояние, на которое перемещается каждая точка фигуры.
Метод подобия.
1. Понятие о подобии фигур в курсе геометрии VIII класса обычно иллюстрируется многочисленными примерами подобных фигур, встречающихся в быту, в науке и технике. Используется и имеющийся у учащихся опыт применения подобия при изготовлении планов и карт на уроках географии; при проведении мензульной съемки, если она была проведена до изучения этой темы; при выполнении рабочих чертежей на уроках черчения; при разметке деталей в школьных мастерских по чертежам, выполненным в некотором масштабе.
Для лучшего усвоения метода подобия при изучении теоретического материала необходимо проводить подготовительную работу, в частности, разъяснять, хотя бы в простейших случаях (треугольники, параллелограммы), условия, определяющие форму фигуры с точностью до подобия. Так как учащиеся должны уметь выполнять построения вспомогательных фигур, подобных искомым, то нужно повторить изученные ранее методы и приемы геометрических построений, в особенности, метод геометрических мест, что можно сделать при изучении пропорциональности отрезков в связи с новым материалом.
Учащиеся, повторив материал, относящийся к методу геометрических мест, легче воспринимают метод подобия. При решении задач методом подобия, как и при решении задач методом геометрических мест, отбрасываем одно из условий, в результате чего задача становится неопределенной. Ее решением при применении метода геометрических мест является бесконечное множество точек, удовлетворяющих оставшимся условиям, а в случае метода подобия получаем бесконечное множество фигур, объединенных одним свойством; все они подобны искомой фигуре. Взяв одну из них, мы с помощью подобного преобразования, учитывая ранее отброшенное условие, получаем искомую фигуру. Эта аналогия помогает лучше усвоить метод подобия.
2. При изучении понятия «центр подобия» и при построении многоугольника, подобного данному, разъясняем учащимся, что соответственные точки всегда лежат на одной прямой, проходящей через центр подобия, а прямая, не проходящая через центр подобия, преобразуется в параллельную ей прямую. После того как учащиеся ознакомятся с построением многоугольника, подобного данному, разбираем сущность метода подобия, решая несложную задачу, в которой были бы ярко выражены характерные признаки этого метода. Например: «Построить треугольник, знай два его угла А и С и высоту hb».
Эту задачу можно решить различными способами, например методом параллельного переноса или методом геометрических мест. Разобрав предлагаемые учащимися решения и повторив сущность применяемых методов, указываем на возможность решения еще одним способом: с применением подобия фигур.
Если не учитывать высоту искомого треугольника, то по двум данным углам мы можем построить бесконечное множество треугольников, но все они будут подобны искомому. Построим один из них, например треугольник А1В1С1 (рис. 50).
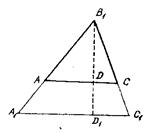
Рис. 50
Чтобы выяснить, будет ли он искомым, проведем высоту BlD1 и сравним ее с данной высотой. В общем случае полученная высота не будет равна данной. Если, например, BlD1 меньше данной высоты в два раза, значит, и стороны треугольника нужно увеличить в два раза, ибо сходственные высоты в подобных треугольниках относятся как сходственные стороны. Если высота BlD1 больше данной в несколько раз, тогда нужно во столько же раз уменьшить и стороны треугольника. Следовательно, треугольник А1В1С1 нужно подобно преобразовать так, чтобы высота была равна данному отрезку hb, для чего достаточно определить коэффициент подобия и выбрать центр подобия. Коэффициент подобия равен отношению данной высоты к настроенной высоте BlD1, то есть 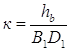 . За центр подобия выберем, например, точку B1, тогда очень легко построить точку, соответствующую точке D1, для чего достаточно отложить отрезок B1D = hв. Проведя прямую СА || С1А1, получим искомый треугольник АВ1С, который действительно удовлетворяет
всем условиям задачи.
. За центр подобия выберем, например, точку B1, тогда очень легко построить точку, соответствующую точке D1, для чего достаточно отложить отрезок B1D = hв. Проведя прямую СА || С1А1, получим искомый треугольник АВ1С, который действительно удовлетворяет
всем условиям задачи.
Построения, выполняемые с применением транспортира и треугольника, просты, доказательство и исследование элементарны, и все внимание учащихся концентрируется на уяснении сущности нового для них способа решения задач на построение.
Повторяем решение задачи: не учитывая высоты, по данным углам построили треугольник, подобный искомому; учитывая затем заданную высоту, подобно преобразовали построенный треугольник в искомый. Такой способ решения задачи называется методом подобия. Этим методом можно решать лишь такие задачи па построение, условия которых можно разбить на две части, одна из которых определяет фигуру с точностью до подобия (два утла треугольника), а вторая часть условия определяет размеры фигуры (высота).
Таким образом, метод подобия при решении задач на построение состоит в следующем; отбросив условие, определяющее размеры фигуры, по оставшимся условиям строим фигуру, подобную искомой; учитывая затем ранее отброшенное условие, подобно преобразовываем построенную фигуру в искомую.
Алгебраический метод.
1. Одним из важных методов, применяемых в школьном курсе геометрии, является алгебраический метод решения задач на построение. Уже в VI-VII классах учащиеся неоднократно применяли алгебру при решении задач вычислительного характера и задач на доказательство с целью упрощения решения. Алгебра дает очень удобный и хороший способ решения геометрических вопросов аналитическим путем.
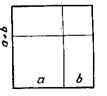 В VI классе целесообразно рассказать, что некоторые сведения по алгебре были известны еще в глубокой древности, но вопросы алгебры не отделялись от вопросов арифметики и геометрии. Позже греческие ученые, такие, как Пифагор, Евклид, которые занимались преимущественно геометрией, получили значительные результаты и в алгебре. Но многие алгебраические тождества доказывались ими геометрически. На доске в качестве примера иллюстрируем доказательство тождества: (a + b)2 = a2 + 2ab + b2 (рис. 56).
В VI классе целесообразно рассказать, что некоторые сведения по алгебре были известны еще в глубокой древности, но вопросы алгебры не отделялись от вопросов арифметики и геометрии. Позже греческие ученые, такие, как Пифагор, Евклид, которые занимались преимущественно геометрией, получили значительные результаты и в алгебре. Но многие алгебраические тождества доказывались ими геометрически. На доске в качестве примера иллюстрируем доказательство тождества: (a + b)2 = a2 + 2ab + b2 (рис. 56).
Рис. 56
Площадь квадрата, построенного на сумме отрезков а и b, равна сумме площадей двух квадратов со сторонами а и b и площадей двух прямоугольников со сторонами а и b. В IX в. н. э. узбекский
ученый Мухаммед-бен-Муса ал-Хорезми написал книгу «Хисаб ал-джебр вал-мукабала», появление которой явилось как бы моментом оформления науки алгебры. В дальнейшем алгебра получила свое самостоятельное развитие и начала оказывать большую помощь при решении различных задач других математических дисциплин, в том числе и геометрии.
2. Алгебраический метод решения задач на построение рассматривается как дальнейшее расширение применения алгебры к геометрии. Как известно, он состоит в следующем. Предположив задачу решенной: 1) Устанавливаем, какой или какие отрезки (в редких случаях углы или дуги) нужно определить, чтобы решить задачу, и обозначаем длины этих отрезков через х, y, z, ..., а длины данных отрезков – через а, b, с, …, то есть вводим обозначения. 2) Из условия задачи, пользуясь известными геометрическими соотношениями между искомыми и данными отрезками, составляем уравнение или систему уравнений. 3) Решаем это уравнение или систему уравнений. 4) Исследуем полученные формулы для неизвестных отрезков по условию задачи. 5) Строим с помощью инструментов искомые отрезки, выраженные полученными формулами через данные отрезки. После того как неизвестные построены, выполняем построения, которые окончили бы решение, проводим доказательство и исследование.
Первые четыре этапа известны учащимся, так как при решении геометрических задач на вычисление и алгебраических на составление уравнений всегда выделялись такие же этапы. Это говорит о том, что задачи на построение, решаемые таким методом, можно рассматривать как обобщение задач вычислительного характера, а с другой стороны, при применении алгебраического метода всякая задача на построение заменяется вначале задачей на вычисление, так что каждая задача на построение, решаемая этим методом, является, по существу, и задачей на вычисление.
4. Целесообразность рассмотрения этого метода в средней школе не определяется только тем, что учащиеся ознакомятся с еще одним видом задач, для решения которых применяется алгебра. Алгебраический метод решения отдельных, даже сложных задач на построение более доступен учащимся, ибо достаточно получить соответствующую формулу для определения искомой величины, чтобы стало ясным все решение задачи.
Алгебраический метод позволяет легко установить условия возможности решения задачи, а также наличие определенного числа решений при тех или иных значениях и положениях данных.
5. Однако в средней школе не следует чрезмерно увлекаться этим методом за счет других важных разделов. Нужно решать доступные и интересные для учащихся задачи.
2.3. Влияние задач на построение на развитие логического мышления.В программе по математике для средней общеобразовательной школы, разработанной в соответствии с Основными направлениями реформы общеобразовательной и профессиональной школы, подчеркивается, что развитие логического мышления учащихся является одной из основных целей курса геометрии.
При изучении геометрии развитие логического мышления учащихся осуществляется в процессе формирования понятий, доказательства теорем, решения задач.
При изучении геометрических построений, прежде всего, приходится преодолевать трудности логического порядка. В условиях школы для преодоления этих трудностей совершенно необходимо сопровождать логические конструкции фактическими построениями при помощи определенных инструментов (линейка, чертежный треугольник, циркуль),а также изображениями, выполняемыми от руки.
Весь процесс решения задачи на построение сопровождается выполнением соответствующих чертежей («чертеж-задание», «чертеж-набросок», «чертеж-построение», «чертеж для исследования»).
Решение задач на построение развивает логическое и активное мышление учащихся. Ни одни задачи не содействуют так развитию в учениках наблюдательности и правильности мышления, представляя в то же время для них и наибольшую привлекательность, как геометрические задачи на построение.
Действительно, задачи вычислительного характера в планиметрии, не требующие в большинстве своем вспомогательных построений и сложных логических рассуждений, служат для закрепления фактического материала: формулировок теорем, свойств фигур и т.п. чтобы развивать логическое мышление учащихся, а этим сделать их знания более систематизированными, прочными и глубокими, решаются задачи на доказательство.
Большое значение для логического развития учащихся имеют и задачи на построение. Наличие анализа, доказательства и исследования при решении большинства таких задач показывает, что они представляют собой богатый материал для выработки у учащихся навыков правильно мыслить и логически рассуждать. При решении задач на построение они имеют дело не с конкретной определенной фигурой, а должны создать необходимую фигуру, подвергающуюся различным изменениям в процессе решения. Вскрывая взаимосвязи между данными элементами, видим, как с изменением одних изменяются другие и даже вся фигура.
Весь комплекс, состоящий из четырех стадий решения задач на построение (анализ, построение, доказательство, исследование), является хорошей школой решения и исследования проблем в области точных наук. В процессе решения таких задач развивается внимание, настойчивость, инициатива и изобретательность.
Логические трудности главным образом связаны с проведением анализа и исследования задачи. Известные методы решения задач на построение изучаются здесь, прежде всего как средства анализа.
3. ПЕДАГОГИЧЕСКИЙ ЭКСПЕРИМЕНТ 3.1. Замысел эксперимента. Программа эксперимента.
Среди учащихся 10-го класса был проведен тест на выполнение логических операций над геометрическими объектами.
Тест предназначен для выявления умения выполнять основные логические операции над геометрическими фигурами (аналогии, классификации, построение закономерности) и рассчитан на работу с учащимися старших классов, студентами математических факультетов.
Материалом заданий являются плоские геометрические фигуры (углы, многоугольники, окружности, комбинированные формы).
Данные тестирования могут использоваться преподавателями математики, практическими психологами для отбора в математические классы и школы для разработки коррекционных обучающих программ в целях дифференциации учащихся.
Тест предназначен для диагностики умственного развития учащихся подросткового и юношеского возраста; позволяет выявлять индивидуально-психологи-ческие различия в овладении логическими операциями с геометрическими объектами. Он содержит три набора заданий (субтестов) на выполнение «аналогии», «классификации», «закономерности построения» геометрических объектов, в качестве которых выступают углы, треугольники, четырехугольники, неоднородные «комбинированные фигуры». Каждый субтест состоит из 12 вариантов заданий, отличающихся усложнением материала.
OCHOBHOE СОДЕРЖАНИЕ И НАЗНАЧЕНИЕ ТЕСТА
Как уже отмечалось, предлагаемый тест может быть использован для диагностики умственного развития учащихся. Критерием этого развитая служит успешность (правильность) выполнения логических операций: «аналогии», «классификации», «закономерности построения» геометрических объектов. Работа с тестом предполагает, что испытуемый знает основные признаки (свойства) геометрических фигур, умеет ими пользоваться. Однако тест не предусматривает проверку программных требований к усвоению учебного материала (знания теорем, аксиом, правил решения задач и т.п.). Он не ориентирован также на проверку графических знаний, умений. Все задания теста даются в готовом виде. Испытуемый выполняет требуемые логические операции, опираясь на восприятие объектов (в виде плоскостных изображений), заданных графически.
Выполнение заданий теста предполагает мысленное преобразование геометрических объектов. Однако содержание и характер этих преобразований теста не определяется построением задания. Поэтому испытуемый может придти к правильному ответу, используя различные мысленные преобразования. При групповом тестировании определяется количество правильно выполненных заданий в целом и в каждом субтесте отдельно. Учитывается также время, затраченное на выполнение, как отдельного задания, так и общего их объема. При индивидуальном тестировании можно оценить не только результативность выполнения заданий теста, но и сам процесс работы. Например, установить, как выполняет испытуемый геометрические преобразования объектов: ориентируется на изменение величины, пространственного положения объектов, осуществляет повороты, достраивание фигуры, произвольно выделяет вписанные и описанные фигуры, меняет соотношение «фигуры и фона» и т.д. Получение таких сведений о работе испытуемых важно для выявления их индивидуальных возможностей для построения коррекционного обучения. Однако это связано с использованием дополнительных методов: специально организованной беседы, контролем за каждым этапом выполняемого преобразования, их анализом, что не может (и не должно) обеспечиваться групповым тестированием.
Данный тест разработан как групповой. Он позволяет выявлять и оценивать каждого учащегося по общей результативности его работы. Однако очень высокие (низкие) результаты могут быть подвергнуты более тщательному и содержательному анализу, что требует индивидуальной работы экспериментатора с каждым учащимся.
Своим содержанием тест «ЛОГО» обеспечивает анализ успешности выполнения трех основных логически операций.
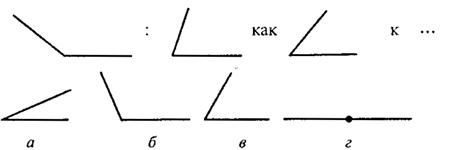
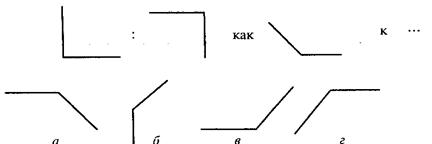
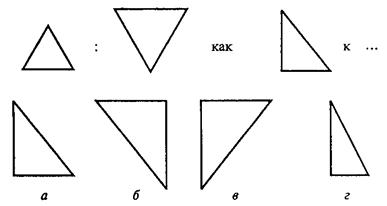
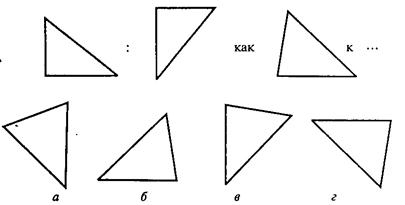
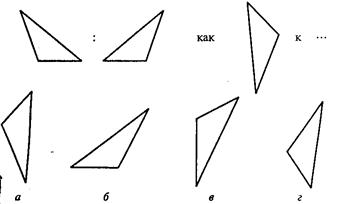
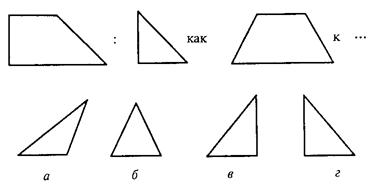
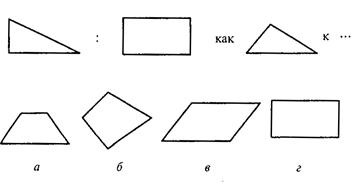
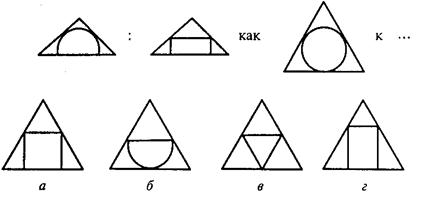
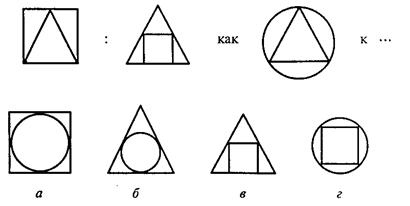
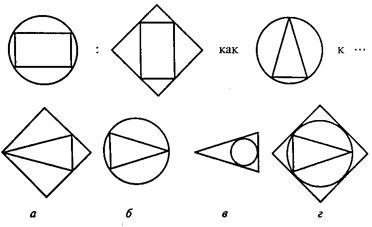
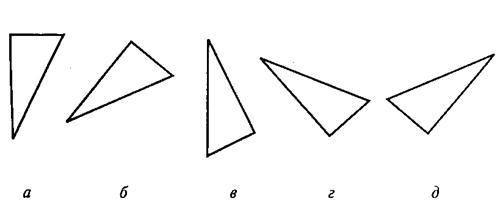
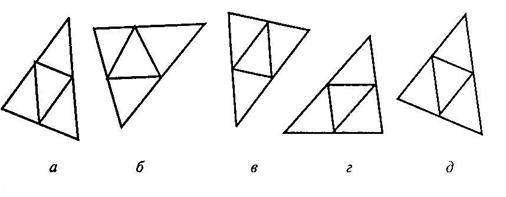
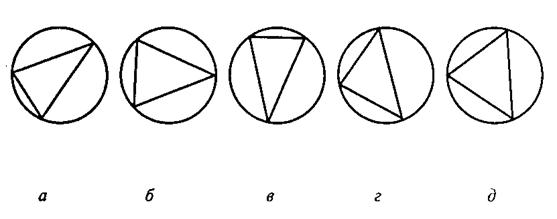
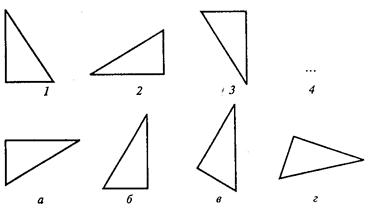
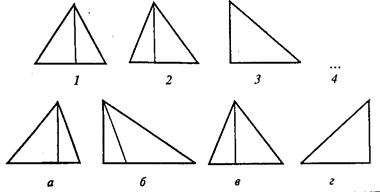
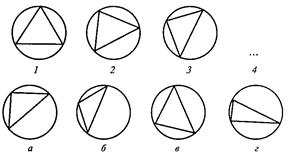
В первом субтесте («аналогия») испытуемому предлагается три однородных геометрических объекта. Между первым и вторым объектами имеется определенная связь, которую испытуемый должен выявить. Сообщается, что между третьим и одним из четырех объектов, предлагаемых на выбор, существует аналогичная связь. Испытуемый должен найти из четырех объектов тот, который соответствует по аналогии третьему. Этот субтест содержит четыре варианта заданий, отличающихся типом геометрических объектов, каждый из которых представлен в трех различных видах.
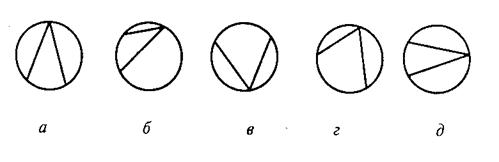
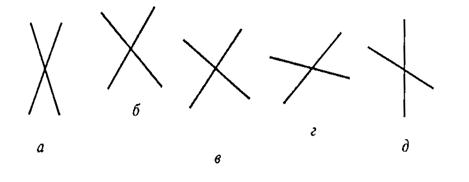
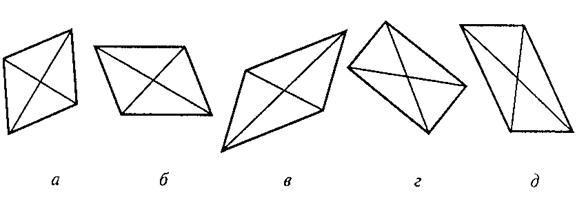
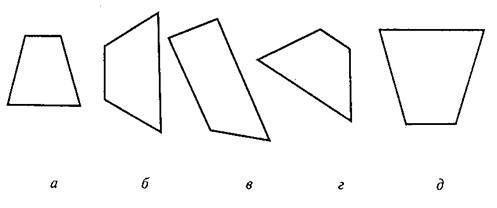
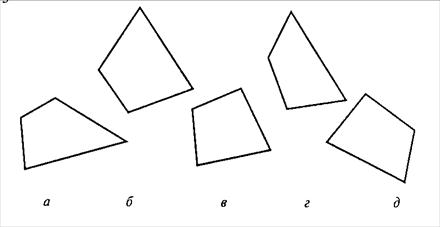
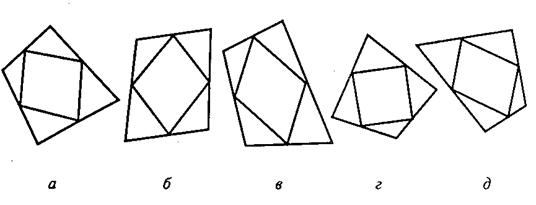
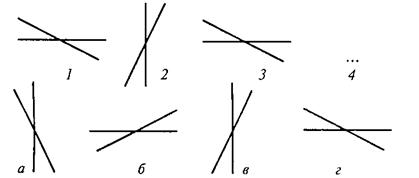
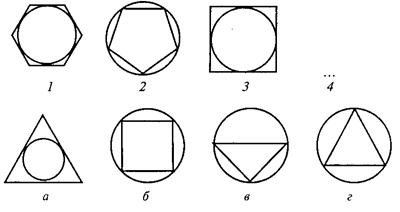
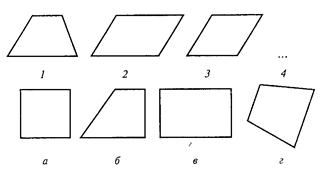
Во втором субтесте («классификация») предлагается пять геометрических объектов, четыре из которых объединены одним общим признаком. Пятый («лишний») объект, который не подходит к остальным, нужно найти. Субтест также имеет несколько вариантов заданий, отличающихся типом геометрических объектов, представленных различным образом.
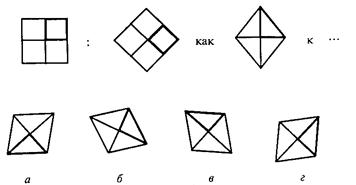
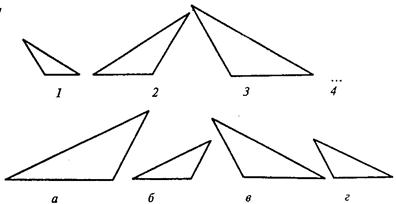
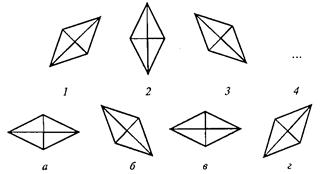
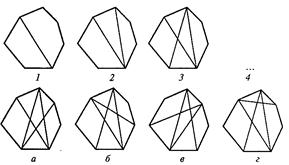
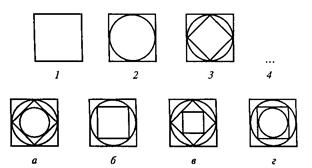
В третьем субтесте испытуемому предлагается три геометрических объекта, расположенных в определенной закономерности. Необходимо найти и использовать эту закономерность, подобрать к трем объектам четвертый, который продолжал бы данную закономерность. Субтест содержит четыре варианта заданий, отличающихся постепенным усложнением типа геометрического объекта (один объект, их сочетание, сложность конфигурации).
Таким образом, каждый субтест включал 12 заданий. Одна форма теста состояла из 36 заданий. Всего по двум эквивалентным формам было разработано 72 задания.
Тест «ЛОГО» позволяет дифференцировать учащихся по умению выполнять основные логические операции над геометрическими объектами (фигурами), что является существенным для овладения математикой. Он может использоваться при отборе учащихся в математические школы, классы с углубленным изучением этого предмета, для оценки логического мышления учащихся. Поскольку оперирование геометрическими объектами существенно не только при усвоении математики, но составляет основу проекционного черчения, тест может использоваться на занятиях графическими дисциплинами.
На работу с тестом отводится 45 минут. Перед началом работы сообщается ее цель и порядок.
3.2. Описание проведения эксперимента и его результаты.Описание и пример работы с субтестом 1.
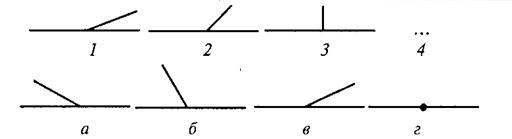
Вам предлагаются три геометрических объекта. Между первым и вторым объектом существует определенная связь. Между третьим и одним из четырех объектов, предлагаемых на выбор, существует аналогичная, та же самая связь. Этот геометрический объект вам следует найти и написать на листке бумаги соответствующую ему букву.
Пример:
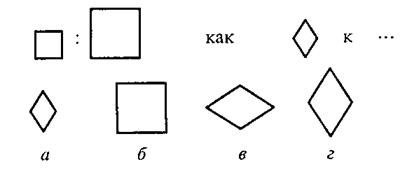
Правильный ответ – г). Его нужно записать.
СУБТЕСТ 1. ЗАДАНИЕ 1
| 1 |
|
| 2 |
|
| 3 |
|
СУБТЕСТ 1. ЗАДАНИЕ 2.
| 1 |
|
| 2 |
|
| 3 |
|
СУБТЕСТ 1. ЗАДАНИЕ 3.
| 1 |
|
| 2 |
|
| 3 |
|
СУБТЕСТ 1. ЗАДАНИЕ 4.
| 1 |
|
| 2 |
|
| 3 |
|
Описание и пример работы с субтестом 1.
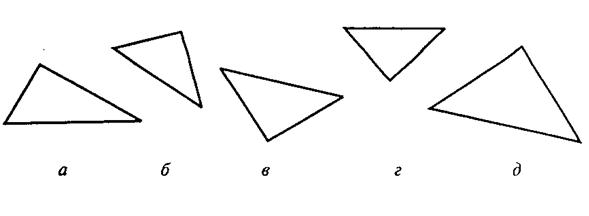
Вам предлагаются ПЯЧЬ геометрических объектов. четыре из них объединены общим признаком. пятый объект к ним не подходит. Его нужно найти и написать на листке бумаги соответствующую ему букву.
Пример:
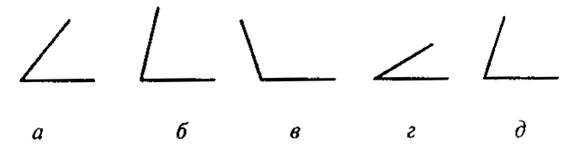
Правильный ответ – в. Его нужно записать.
СУБТЕСТ2. ЗАДАНИЕ 1
| 1 |
|
| 2 |
|
| 3 |
|
СУБТЕСТ 2. ЗАДАНИЕ 2.
| 1 |
|
| 2 |
|
| 3 |
|
СУБТЕСТ 2. ЗАДАНИЕ 3.
| 1 |
|
| 2 |
|
| 3 |
|
СУБТЕСТ 2. ЗАДАНИЕ 4.
| 1 |
|
| 2 |
|
| 3 |
|
Описание и пример работы с субтестом 3.
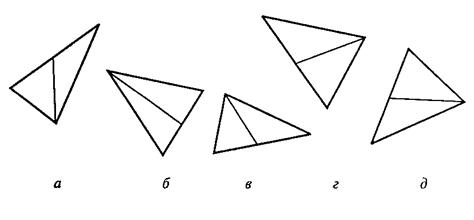
Вам предлагаются три геометрических объекта, расположенных на основе определенной закономерности. Вам нужно выбрать из представленных внизу вариантов ответов четвертый объект, который продолжал бы данную закономерность построения геометрического ряда, и написать на листке бумаги соответствующую ему букву.
Пример:
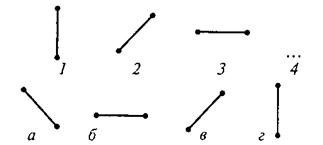
Правильный ответ – а. Его нужно записать.
ФОРМА А. СУБТЕСТ 3. ЗАДАНИЕ 1.
| 1 |
|
| 2 |
|
| 3 |
|
СУБТЕСТ 3. ЗАДАНИЕ 2.
| 1 |
|
| 2 |
|
| 3 |
|
СУБТЕСТ 3. ЗАДАНИЕ 3.
| 1 |
|
| 2 |
|
| 3 |
|
СУБТЕСТ 3. ЗАДАНИЕ 4.
| 1 |
|
| 2 |
|
| 3 |
|
КЛЮЧ К РЕШЕНИЮ ЗАДАНИЙ
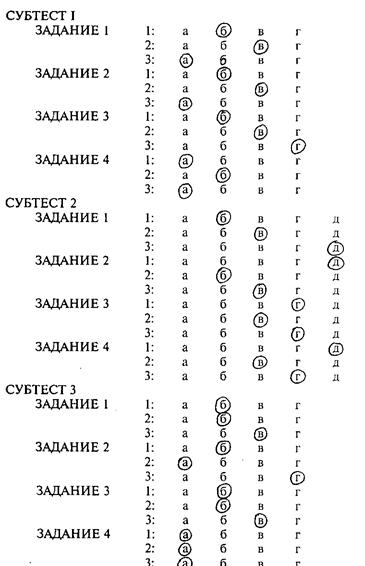
Обработка результатов тестирования
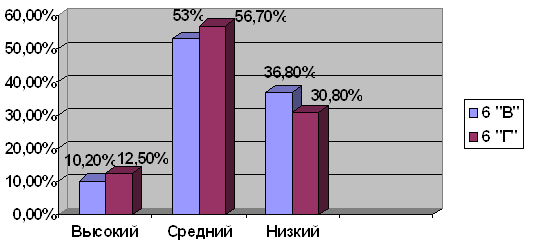
По итогам количественной обработки теста получили следующие результаты:
| Фамилия учащегося | Кол-во правильно выполненных заданий | Процентное отношение |
| Антонова К. | 10 | 28% |
| Колосова Н. | 10 | 28% |
| Михайлюк К. | 18 | 50% |
| Назарова А. | 20 | 56% |
| Петрова К. | 16 | 44% |
| Платонова Ю. | 21 | 58% |
| Трофимова О. | 12 | 33% |
Далее мы провели качественную обработку тестирования, выяснив:
Похожие работы
... учебник и задачник / А. П. Кисилев, Н.А. Рыбкин. – М.: Дрофа, 1995. 9. Изучение личности школьника / под. ред. Л.И. Белозеровой. – Киров, Информационный центр, 1991. 10. Коновалова, В.С. Решение задач на построение в курсе геометрии как средство развития логического мышления / В.С. Коновалова, З.В. Шилова // Познание процессов обучения физике: сборник статей. Вып.9. – Киров: Изд-во ...
... и перенести полученные знания на практику. Глава 2. Работа учителя по развитию логического мышления на уроках математики 2.1 Опытно-экспериментальная работа и анализ ее результатов Опытно-экспериментальное исследование по выявлению уровня развития логического мышления школьников при решении текстовых задач проводилось на базе МОУ «Средняя общеобразовательная школа № 10» г. Кунгура в ...
... перед ними задачи; выделить основные этапы решения проблемной ситуации; провести обзор основных типов заданий для развития логического мышления на уроках информатики. Глава 1. Мышление 1.1 Основные закономерности развития мышления Развивающее обучение в широком смысле слова означает совокупное формирование умственных, волевых и эмоциональных качеств личности, способствующих ее ...
... работы у испытуемых экспериментальной группы произошло повышение уровня логического мышления. Такие изменения могут рассматриваться как правильная организация процесса развития логического мышления у младших школьников в процессе рисования с натуры. Выявленные статистически значимые различия в динамике большинства исследованных в экспериментальных и контрольной групп, подтвержденные качественно- ...
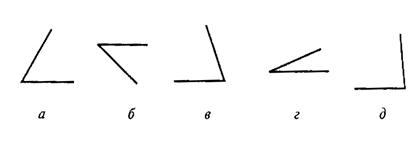
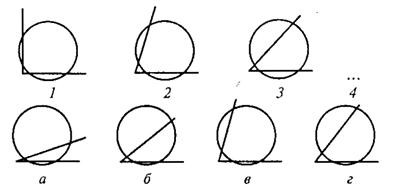





0 комментариев