МЕТОДИКА ОБУЧЕНИЯ РЕШЕНИЮ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ НА ПОСТРОЕНИЕ, С ЦЕЛЬЮ РАЗВИТИЯ ЛОГИЧЕСКОГО МЫШЛЕНИЯ УЧАЩИХСЯ
Обучающая роль математических задач
Все учащиеся без исключения не могут мысленно создать образ предмета и рассмотреть его с разных сторон «в воображении»
Осевая симметрия – это первый из видов движения, преобразования, с которым учащиеся встречаются в
систематическом курсе геометрии
Вид заданий (на величину, форму и тип оперирования образами), который вызывает наибольшее количество ошибок;
Задачу рекомендуется решить в классе. Если она будет задана на дом, то следует дать указание: решение начать с построения окружности
Навигация
Задачу рекомендуется решить в классе. Если она будет задана на дом, то следует дать указание: решение начать с построения окружности
Развитие логического мышления учащихся при решении задач на построение
249522
знака
15
таблиц
58
изображений
19. Задачу рекомендуется решить в классе. Если она будет задана на дом, то следует дать указание: решение начать с построения окружности.
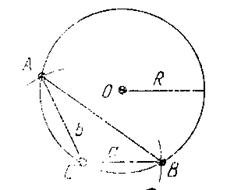
Рис. 2
Дано: а, b, R.
Решение. Проведем окружность данного радиуса (рис. 2). Выберем на окружности точку С и из этой точки как из центра сделаем две засечки радиусами а и b. Получим точки А и В. Δ АВС искомый. У него данные попоны ВС = а, АС = b. Описанная окружность имеет радиус R.
Для того чтобы задача имела решение, стороны а и b должны быть меньше диаметра окружности (a<2R, b<2R).
20. Дано: R, точки А, В.
Решение. Проведем две окружности радиуса R с центрами в точках А и В. Точки пересечения этих окружностей являются центрами искомой окружности.
Исследование. Если АВ > 2R, то задача не имеет решения.
Если АВ = 2R, то задача имеет одно решение: центр окружности – середина отрезка АВ.
Если АВ<2R, то задача имеет два решении: обе точки пересечения проведенных окружностей служат центрами искомых окружностей.
На примере этой задачи учащимся можно дать представление об этапе исследования, о различном числе решений задач на построение. Для этого целесообразно решить задачу 20 в классе, заготовив на доске три исходных рисунка: отрезок, равный R, и точки А и В, причем: 1) АВ<2R; 2) АВ = 2R; 3) АВ > 2R. Решение у доски одновременно проводится силами трех учащихся.
Примечание. Задачу можно предложить учащимся также после изучения теоремы 5.6, решив се с помощью метода геометрических мест.
ТЕМА 2. ПОСТРОЕНИЕ УГЛА, РАВНОГО ДАННОМУ (1 ч)
Комментарий для учителя
В результате изучения пункта учащиеся должны:
знать алгоритм задачи на построение угла, равного данному;
уметь применять алгоритм при решении задачи на построение треугольников по двум сторонам и углу между ними, по стороне и двум углам и т. п.
Методические рекомендации к изучению материала
Начать изучение нового материала можно с решения задачи на построение треугольника типа 21 (1, а):
«Постройте треугольник АВС по двум сторонам и углу между ними: АВ = 5 см, АС = 6 см, 
А = 400».
Решение этой задачи знакомо учащимся из курса математики VI класса.
Затем можно предложить учащимся решить ту же задачу, однако данные задать геометрически:
«Постройте треугольник АВС по двум сторонам с, b и углу между ними 
» (рис. 3).
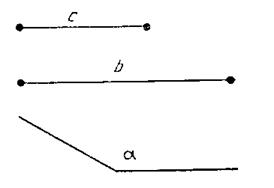
Рис. 3
Для того чтобы решить эту задачу, нам надо построить угол А, равный данному углу .
Далее учащимся излагается алгоритм решения задачи 5 (2).
После этого можно предложить учащимся решить задачу:
«Постройте равнобедренный треугольник по основанию и углу, прилежащему к основанию».
Примерное планирование изучения материала
В классе – разобрать решения задач 5 (2), 21 (1 а; 2 б), 22 (2); дома – вопрос 11. задачи 22 (1). 23.
Указания к задачам
К пункту относятся задачи 21–23.
ТЕМА 3. ПОСТРОЕНИЕ БИССЕКТРИСЫ УГЛА.
ДЕЛЕНИЕ ОТРЕЗКА ПОПОЛАМ (1 ч)
Комментарий для учителя
В результате изучения пунктов учащиеся должны:
знать алгоритмы решения задач на деление угла и отрезка пополам;
уметь решать несложные задачи па построение с использованием этих алгоритмов.
Методические рекомендации к изучению материала
1°. При изложении учащимся решения задачи 5.3 (построение биссектрисы угла) можно более подробно остановиться на доказательстве того факта, что в результате построения действительно получились равные утлы.
В самом деле, Δ АВD = ΔАСD по третьему признаку равенства треугольников. Из их равенства следует, что DAB = DAC (рис. 4).
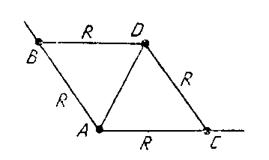
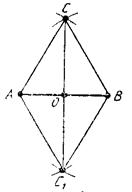
Рис. 4 Рис. 5
2о. При решении задачи на деление отрезка пополам (задача 5.4) отрезки АС, ВС, АС1 и ВС1 строятся равными отрезку АВ (рис. 5). При доказательстве этот факт не учитывается. Действительно, равенство треугольников САС1 и СВС1 по третьему признаку можно доказать и без этого. Можно доказать, что точка О – середина отрезка АВ и с учетом конкретного построения, данного в учебном пособии. Приведем это доказательство. По построению АС = СВ = АС1 = С1В = АВ, т. е. ΔАСВ и ΔАС1В равносторонние; следовательно, САВ = С1АВ = 60°, а САС1 = 120о. ΔАСС1 равнобедренный, АСС1 = АС1С = (1800 – 1200):2 = 300, ВСО = АСВ – АСС1 = 600 – 300 = АСС1, т. е. СО – биссектриса угла С в равнобедренном треугольнике АВС: следовательно, она медиана: ВО = АО.
30. Для закрепления изученных приемов построения можно дать следующие задачи:
1. Дан треугольник. Постройте одну из его медиан (задача 28).
2. Постройте с помощью циркуля и линейки утлы 60° и 30° (задача 25).
Примерное планирование изучения материала
В классе – разобрать решения задач 5.3 и 5.4, решить задачи 25, 28; дома – вопросы 12, 13, задачи 24, 28 (еще две медианы).
Указания к задачам
К пунктам относятся задачи 24–29.
ТЕМА 4. ПОСТРОЕНИЕ ПЕРПЕНДИКУЛЯРНОЙ ПРЯМОЙ (1 ч)
Комментарий для учителя
В результате изучения пункта учащиеся должны:
знать алгоритм построения перпендикулярной прямой;
уметь его применять при решении несложных задач на построение.
Методические рекомендации к изучению материала
10. Можно предложить учащимся другое доказательство справедливости выполненного построениЯ.
Первый случай (рис. 6) (точка О лежит на прямой а). Отрезки АО = ОВ, АС = СВ по построению. Следовательно, ΔАВС равнобедренный, а СО – медиана этого треугольника, т. е. высота (теорема 3.5): СО
АВ.
Второй случай (рис. 7) (точка О не лежит на прямой).
ΔАОО1 = ΔВОО1 по третьему признаку. Из равенства этих треугольников следует: АОС= ВОС. В
равнобедренном ΔАОВ ОС – биссектриса и, следовательно, высота.
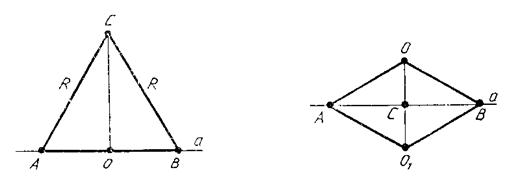
Рис. 6 Рис. 7
2°. Сразу после разбора задачи 5.5 можно выполнить с учащимися следующие упражнения;
1) Дан треугольник. Постройте одну из его высот (часть задачи 28).
2) Постройте прямоугольный треугольник по его катетам.
3) Задача 30.
Решение задачи 30 является составной частью решения задач 31-34.
Примерное планирование изучения материала
В классе – провести самостоятельную работу, разобрать решение задачи 5.5, решить задачу 30; дома – вопрос 14, задача 28 (две другие высоты).
Похожие работы
... учебник и задачник / А. П. Кисилев, Н.А. Рыбкин. – М.: Дрофа, 1995. 9. Изучение личности школьника / под. ред. Л.И. Белозеровой. – Киров, Информационный центр, 1991. 10. Коновалова, В.С. Решение задач на построение в курсе геометрии как средство развития логического мышления / В.С. Коновалова, З.В. Шилова // Познание процессов обучения физике: сборник статей. Вып.9. – Киров: Изд-во ...
... и перенести полученные знания на практику. Глава 2. Работа учителя по развитию логического мышления на уроках математики 2.1 Опытно-экспериментальная работа и анализ ее результатов Опытно-экспериментальное исследование по выявлению уровня развития логического мышления школьников при решении текстовых задач проводилось на базе МОУ «Средняя общеобразовательная школа № 10» г. Кунгура в ...
... перед ними задачи; выделить основные этапы решения проблемной ситуации; провести обзор основных типов заданий для развития логического мышления на уроках информатики. Глава 1. Мышление 1.1 Основные закономерности развития мышления Развивающее обучение в широком смысле слова означает совокупное формирование умственных, волевых и эмоциональных качеств личности, способствующих ее ...
... работы у испытуемых экспериментальной группы произошло повышение уровня логического мышления. Такие изменения могут рассматриваться как правильная организация процесса развития логического мышления у младших школьников в процессе рисования с натуры. Выявленные статистически значимые различия в динамике большинства исследованных в экспериментальных и контрольной групп, подтвержденные качественно- ...
0 комментариев