За кількістю невідомих у структурі задач. Ю.М. Колягін пропонує їх класифікувати на навчальні, пошукові та проблемні

1. За кількістю невідомих у структурі задач. Ю.М. Колягін пропонує їх класифікувати на навчальні, пошукові та проблемні.

2. За характером об'єктів задачі поділяють на практичні та математичні.

3. За відношенням до теорії виділяють стандартні та нестандартні задачі. У ролі основної ознаки стандартних задач вказано наявність у курсі математики таких загальних правил і положень, що однозначно визначають програму розв'язання цих задач та виконання кожного кроку цієї програми (тобто мають свій алгоритм розв'язування). Нестандартні задачі - це такі, для яких у курсі математики не існує загальних правил або положень, що визначають точну програму їх розв'язання.

4. За функціями у процесі навчання розрізняють дидактичні, пізнавальні та розвиваючі задачі. Задачі з дидактичними функціями використовують для підготовки учнів до введення нового матеріалу, а також при його закріпленні: вони несуть функцію застосування теорії, що вивчається. Задачі з пізнавальними функціями мають за мету відпрацювати та поглибити основний зміст математичної дисципліни. Задачі з розвиваючими функціями – це ті, розв'язування яких потребує певних знань та вмінь, не передбачених програмою. Саме ці задачі спрямовані на розвиток мислення.

5. Задачі, що стимулюють навчально-пізнавальну діяльність; організують та здійснюють навчально-пізнавальну діяльність учнів; задачі, у процесі виконання яких здійснюється контроль та самоконтроль ефективності навчально-пізнавальної діяльності.

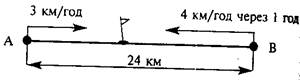
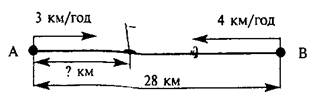
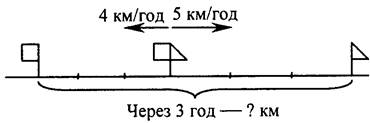
6. Задачі для початкової школи класифікують за змістом: задачі на рух, задачі на пропорційне ділення, на знаходження четвертого пропорційного.

7. За характером вимоги у початковому курсі математики виділяють задачі на обчислення, задачі на побудову, задачі текстові, задачі комбінованого характеру.

Наведені класифікації дозволяють ширше уявити собі проблеми, пов'язані з методикою навчання молодших школярів розв'язувати задачі, спрямовуючи цей процес на розвиток мислення.

Загалом задачі у початковому курсі математики класифікують на прості і складені. При цьому до простих належать 25 видів задач (на розкриття змісту арифметичних дій; на розкриття відношень між числами; задачі, що розкривають зв’язки між компонентами і результатами арифметичних дій; задачі на збільшення (або зменшення) числа на кілька одиниць ( чи в кілька разів) та ін.) [3, 106-107].

Прості задачі часто використовуються початковому курсі математики і при ознайомленні учнів з іншими сюжетами задач у справі формування в дітей уявлень про величини, їх вимірювання, про зв’язки, які існують між такими величинами, як ціна, кількість і вартість; маса одного предмета, число предметів і загальна маса; швидкість, час і пройдений шлях; довжина і ширина прямокутника та його площа; норма виробітку за одиницю часу, затрачений час і загальний виробіток, норма витрати яких-небудь матеріалів на один виріб, число виробів і загальна витрата матеріалів на них тощо [17, 3]. Такі задачі розглядаються в 1-4 класах поступово, в міру розширення кола величин, що вводяться у зв’язку з вивченням відповідних питань і на матеріалі інших вправ.

Аналогічно до того, як прості задачі використовуються для створення наочної опори при розгляді таких питань теорії, як, скажімо, зв’язок між компонентами і результатами дії, значна група складених задач допомагає дітям усвідомити властивості розглядуваних дій. Це задачі, які ілюструють властивості додавання і віднімання, що вивчаються в I класі, а також властивості множення й ділення, розглядувані в II – IV класах.

Складені задачі, як і прості, використовуються і під час ознайомлення з деякими новими поняттями, новими випадками дій, вони допомагають дітям усвідомити нові для них поняття дробу числа й інші питання курсу [23, 51].

Складені арифметичні задачі відіграють важливу роль у навчанні дітей тих загальних прийомів розумової діяльності, які необхідні для розв’язання будь-якої задачі:

а) аналізувати, виділити відоме і невідоме;

б) встановлювати зв’язки між даними і шуканим;

в) складати план розв’язування;

г) перекладати залежності між даними і шуканим, сформульовані в задачі словами, на мову математичних виразів, рівностей, рівнянь;

д) виконувати відповідні дії (розв’язувати відповідні рівняння) і знаходити відповідь на запитання задачі;

е) перевіряти розв’язання [51, 32].

Складені задачі використовують як наочну конкретну основу для розгляду нових понять, властивостей дій. Цією функцією визначається й місце їх у загальній системі курсу: вони вводяться тоді, коли розглядаються відповідні питання, і в такій кількості, яка потрібна для пояснення нових питань. При цьому спеціальної мети навчити дітей розв’язувати задачі двома способами не ставиться. Важливіше, щоб вони могли розв’язати її раціональним способом.

Інша група складених задач, що займають велике місце в підручниках для початкових класів школи, пов’язана з роботою над різними кількісними відношеннями. Такі задачі вводяться після того, як діти достатньо засвоять кількісні відношення і навчаться застосовувати свої знання під час розв’язування простих задач, які містять слова “на стільки-то (у стільки-то разів) більше (менше)” в різному контексті.

Складені задачі дають можливість продовжити і розширити та поглибити роботу, спрямовану на ознайомлення дітей з різними величинами і залежністю між ними [62, 23].

Група складених задач, пов’язаних з необхідністю застосувати знання зв’язку між такими величинами, як ціна, кількість, вартість, займає важливе місце в підручниках для всіх чотирьох класів. Спеціальна увага приділяється задачам, які розкривають зв’язки між цими величинами в I – IV класах [35, 4].

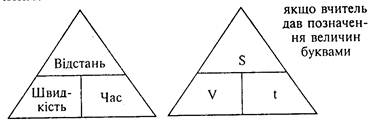
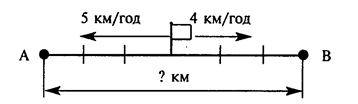
У IIІ класі вводиться ряд нових величин (норма витрачання матеріалу на виріб, число виробів, загальна витрата матеріалу; норма виробітку за одиницю часу, витрачений час і загальний виробіток); у IV класі діти ознайомлюються із зв’язками між швидкістю, часом і відстанню при рівномірному русі, із зв’язком між сторонами прямокутника і його площею. Усі ці нові питання розглядаються не лише на основі практичних робіт, пов’язаних із спостереженнями, вимірюваннями, а й на матеріалі розв’язування різноманітних сюжетних задач, що показують, для яких практичних питань потрібні здобуті знання, вивчені взаємозв’язки між величинами.

Складені задачі поділяють за кількістю дій, якою розв’язується та чи інша задача. Це задача на дві, три, чотири дії. Трьома діями розв’язуються задачі, які утворилися розширенням задач на дві дії; також до цього типу належать також задачі на знаходження суми двох добутків, різниці двох добутків, різниці двох часток і т. ін. [51, 87].

Метою роботи над задачами є не тільки засвоєння способів їх розв'язування, а головним чином формування умінь, необхідних для самостійного розв'язування задач програмного мінімуму та подальшого навчання. У підручниках для 1—4 класів є такі задачі, які традиційно називають типовими, а також задачі з конкретним змістом. До типових належать задачі на знаходження четвертого пропорційного (на спосіб прямого і оберненого зведення до одиниці та спосіб відношень), на пропорційне ділення, на знаходження числа за двома різницями, на знаходження середнього арифметичного. Методика розв'язування типових задач принципово не відрізняється від розгляду будь-яких інших задач нового виду, тобто включає підготовку, ознайомлення і розвиток умінь [7, 29]. Проте деякі особливості роботи над типовими задачами необхідно враховувати.

Зазначені типові задачі пов'язані з пропорційними величинами. Розв'язування їх ґрунтується на знанні відповідних зв'язків між величинами. Ознайомлення з величинами провадиться одночасно з розкриттям зв'язків між ними. Зв'язки формулюються у вигляді висновків. Наприклад, якщо відомо ціну і кількість, то вартість можна знайти дією множення. Типові задачі мають деякі характерні ознаки, які враховуються на підготовчому етапі роботи. Необхідно також враховувати взаємозв'язки між окремими типовими задачами. Особливу увагу слід приділити задачам на знаходження четвертого пропорційного до трьох даних.

Розв'язування задач на знаходження четвертого пропорційного способом зведення до одиниці запроваджується в 3 класі. Розгляду задач передує тривала робота над їх розв'язуванням на визначення ціни, кількості та вартості. Вона проводиться у вигляді гри "в магазин" [8]. Під час гри учні вчаться розв'язувати задачі на знаходження вартості. ціни і кількості. Характерною особливістю в цій роботі є те, що, аналізуючи задачі, вчитель вимагає від учнів пояснення, які величини відомі і які треба знайти.

Розв'язування задач на знаходження середнього арифметичного ґрунтується на правилі: щоб знайти середнє арифметичне кількох чисел, треба їх суму поділити на кількість цих чисел. Це правило вводиться на основі аналізу готового розв'язання задачі.

Ознайомлення дітей із задачами на пропорційне ділення проводять у 4 класі. Спочатку вони виконують підготовчі завдання [7, 31].

У початковому курсі математики арифметичні задачі використовуються протягом усіх чотирьох років початкового навчання. Система їх розміщення, природно, збігається з логікою розгортання понять, що вводяться, ознайомлення з арифметичними діями і їх властивостями тощо. Особливість задач, які для цього відбираються, максимальна їх простота. Вони мають бути цілком зрозумілі, близькі дітям за сюжетом, просто викладені, без будь-яких незрозумілих, нових для дітей слів, які б потребували додаткових пояснень. Саме цій меті підпорядкована більша частина задач, широко представлених у програмі і в підручниках для кожного року навчання.

Оскільки в 1 класі діти вперше ознайомлюються з діями додавання і віднімання, а в 2 з діями множення і ділення, то тут передбачається використання простих текстових задач, насамперед спрямованих на розкриття змісту цих дій. Жодного означення дій у початкових класах не вводиться, і тому їх зміст діти мають усвідомити, головним чином, на основі практичних операцій з різними множинами предметів і в процесі розв’язування відповідних простих сюжетних задач, що дають змогу перевести ці операції в план розумових дій [39, 134].

Отже, добір і розміщення текстових задач для 1-4 класів підлягає логіці розгляду нових питань арифметичної теорії і відповідає вимозі поступового ускладнення завдань, що зумовлюється деякими особливостями форми подання математичних зв’язків і відношень, які визначають вибір арифметичної дії, необхідної для розв’язування задачі. Ускладнювати завдання можна, ввівши нові величини, розглядаючи з дітьми нові для них зв’язки.

Однією з функцій складених задач є розвиток здобутих знань, удосконалення їх у процесі застосування в змінених умовах. Але складені сюжетні задачі, введено в початковий курс математики не лише для цього. Одна з їх функцій – навчити дітей “перекладу” словесно заданих відношень і зв’язків між різними величинами, числами, на мову математичних виразів, рівностей, рівнянь. Цій меті підпорядковані і добір задач, і система їх розміщення в часі, і методика роботи над ними.

Ця система забезпечує поступовий перехід від простого до дедалі складнішого: від складання простих виразів і рівнянь у процесі розв’язання задач на одну дію до складання виразів з 2-3 діями при розв’язуванні досить легких за структурою складених задач. Поступове наростання труднощів у таких вправах можливе тільки тоді, коли вчитель розуміючи завдання, що стоять перед ним, використовуватиме для цього пропоновані вправи з підручника [23, 54].

Лише вчитель може визначити, яку задачу і коли можна запропонувати дітям, яке завдання доцільно пов’язати з розв’язуванням цієї задачі: в одному разі досить вказати дію, за допомогою якої розв’язується задача, в іншому – скласти за нею вираз чи рівняння, ще в іншому – доцільно розібрати хід розв’язування за діями, послідовно з’ясовуючи роль кожної з них і коментуючи здобуті результати.

Отже, серед типових складених задач важливе місце займають задачі на пропорційне ділення. Саме цей вид задач є предметом нашого дослідження.

Похожие работы

Формування в учнів умінь розв’язувати задачі на рух

Скачать

128328

9

13

... робити схеми аналітичного або синтетичного способу розбору задач, хоча це не належить до обов'язкових умінь, наведених у програмі з математики для 1–4 класів. 2. Формування умінь учнів розв’язувати задачі на рух   2.1 Аналіз системи задач на рух у початковому курсі математики Вивчення всіх питань програми з математики пов'язане з розв'язуванням арифметичних задач. З одного боку, вони є ...

Формування у другокласників умінь розв’язувати складені задачі

Скачать

136667

5

2

... школярів математичних уявлень і понять. Усвідомлення їх є важливим як для практично-життєвої підготовки учнів, так і для подальшого засвоєння математичних знань у середніх класах. 1.2 Проблема формування вмінь у другокласників розв’язувати складені задачі Традиційно ознайомлення з поняттям “складена задача” здійснюється в 2-му класі на задачах на знаходження остачі, й ці задачі пропонуються ...

Організація самостійної роботи на уроках у початковій школі

Скачать

84377

6

4

... і дії і якості зі взірцем. 2. Характеристика дидактичних умов організації самостійної роботи у початкових класах та їх експериментальна перевірка   2.1 Організація самостійної роботи на уроці у початковій школі Самостійна робота на уроці – органічна частина навчального процесу. Тому методика її проведення визначається специфічними особливостями кожного предмета, змістом теми, рівнем пі ...

Методика роботи над простими задачами, що розкривають конкретний зміст арифметичних дій

Скачать

111172

0

2

... –2007 навчальний рік) була визначена сфера і проблема дослідження; вивчалася педагогічна, методична література з даної теми; аналізувалася робота вчителів початкових класів у галузі методики розв’язування простих задач, що розкривають конкретний зміст арифметичних дій, шляхом диференційованого навчання; формулювалася гіпотеза та завдання дослідження. В процесі експериментального етапу (2007–2008 ...