Навигация
Ступені роботи над текстовими задачами
1.2 Ступені роботи над текстовими задачами
Розв'язати математичну задачу – це значить знайти таку послідовність загальних положень математики (означень, аксіом, теорем, правил, законів, формул), використовуючи які до умов задачі чи до їх наслідків (проміжних результатів розв'язання), одержуємо те, що вимагається в задачі, - її відповідь.
Вченими обґрунтовано, що психологічною основою формування вмінь розв’язувати текстові задачі є основні положення теорії поетапного формування розумових дій (О.М. Леонтьєв, П.Я. Гальперін, Н.Ф. Тализіна та ін.) у синтезі з основними положеннями асоціативно-рефлекторної теорії (Д.Н. Богоявленський, Є.Н. Кабанова-Меллер, Н.О. Менчинська та ін.). Уміння розв’язувати текстові задачі виробляються ефективно, якщо:
1) подавати повну орієнтовну основу дій;
2) при первинному поясненні розгорнуто подавати зразок розв’язування задачі з фіксацією складових операцій;
3) опрацьовувати виконання окремих дій, які входять до складу загального вміння шляхом розв’язання спеціальних вправ;
4) використовувати різні види моделей задачної ситуації;
5) забезпечувати різні види діяльності (репродуктивну, продуктивну, творчу) та тривалість процесу формування вміння [4, 43].
Робота над задачами не повинна зводитись до формування навичок розв’язування задач спочатку одного виду, потім другого і т. д. Основна мета – навчити дітей свідомо встановлювати певні зв’язки між даними і шуканим у різних життєвих ситуаціях, передбачаючи поступове ускладнення їх. Щоб добитися цього, вчитель повинен передбачити в методиці навчання розв’язування задач одного виду різні ступені, які мають свою мету.
На першому ступені вчитель готує дітей до розв’язування задач розглядуваного виду. На цьому ступені учні повинні засвоїти зв’язки, на основі яких вони вибиратимуть дії в процесі розв’язування таких задач.
На другому ступені вчитель ознайомлює учнів з розв’язуванням задач розглядуваного виду. Тут учні навчаються встановлювати зв’язки між даними і шуканим і на цій основі вибирати арифметичні дії, тобто вони навчаються переходити від конкретної ситуації, вираженої в задачі, до вибору відповідної арифметичної дії. Внаслідок такої роботи учні ознайомлюються з способом розв’язування задач цього виду.
На третьому ступені вчитель закріплює вміння розв’язувати задачі розглядуваного виду. На цьому ступені учні мають навчитися розв’язувати будь-яку задачу розглядуваного виду незалежно від її конкретного змісту, тобто вони мають узагальнити спосіб розв’язування задач цього виду [29, 19-20].
Узагальнено структура процесу розв’язування задач подана на рис.
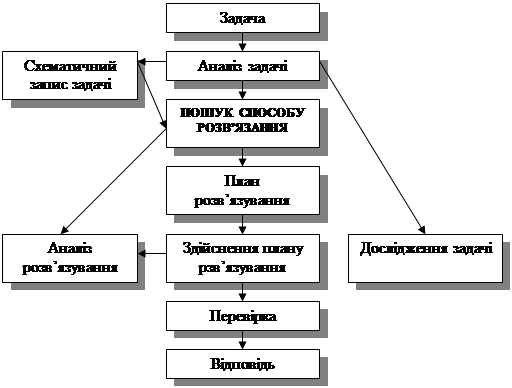 |
Рис. Структура процесу розв’язування задачі
Розглянемо докладніше методику роботи на кожному з названих ступенів [8, 213-214].
Підготовча робота до розв’язування задач того чи іншого виду (перший ступінь) залежить від того, на який зв’язок між даними і шуканим треба спиратися під час вибору арифметичних дій. Відповідно до цього виконують спеціальні вправи.
1. Перед розв’язуванням задач у багатьох випадках виконують операції над множинами. Під час ознайомлення з розв’язуванням більшості простих задач повинні виконуватись вправи на оперування множинами. Елементами множин мають бути конкретні предмети (палички, геометричні фігури вирізані з паперу, самі учні, рисунки тощо.). Наприклад, до введення простих задач на знаходження суми пропонують вправи на об’єднання множин.
Дістаньте картинки, де намальовані курчата. (Діти виконують). На подвір’ї було 3 курчат. До них прибігли ще 2 курчат. Скільки тепер курчат? (Діти лічать картинки). Ми до 3 додали 2 (показує на картинки) і дістали 5.
Підготовкою до розв’язування задач на віднімання буде виконання операції вилучення частини певної множини, на множення – виконуються операції об’єднання рівно чисельних множин, на ділення – поділ множин на рід рівно чисельних множин.
За допомогою операції над множинами розкривають зміст виразів “більше на...”, “менше на...”, “більше в кілька разів...”, “менше в кілька разів...”, що є підготовкою для введення задач, пов’язаних з поняттям різниці та кратного відношення.
2. Більшість арифметичних задач пов’язана з величинами (довжина, час, маса, місткість тощо), тому треба ознайомити дітей із цією величиною. Також дітям корисно для подальшої роботи записувати в окремі зошити чи блокноти значення деяких величин: ціни на окремі товари, швидкості різних видів транспорту, відстані між містами чи найближчими селищами тощо.
3. Арифметичні дії під час розв’язування багатьох задач вибирають на основі зв’язків, які існують між величинами. Щоб у процесі вибору дій діти використовували і усвідомлювали ці зв’язки, потрібно розкрити зв’язки між величинами, розв’язуючи задачі на основі їх конкретного змісту.
Щоб учні засвоїли той чи інший зв’язок, треба організувати цілеспрямовані спостереження. Щоб розкрити зв’язок між ціною, кількістю і вартістю, доцільно організувати екскурсію в магазин, де учні ознайомляться з ціною, запишуть ціни на деякі товари в свої довідники і будуть спостерігати процес купівлі-продажу. Потім на уроці діти складуть ряд простих задач на знаходження вартості за відомою ціною і кількістю, розв’яжуть їх, опираючись на знання конкретного змісту дії множення. Розглянувши розв’язування, учні помітять, що коли відомо ціну і кількість, то вартість знаходять дією множення.
4. Розв’язування складених задач зводиться до розв’язування ряду простих, тому підготовкою до розв’язування складених задач буде навчання розв’язування простих задач.
Розгляду кожного окремого виду задач має передувати спеціальна підготовча робота. Провівши відповідну підготовчу роботу, можна перейти до ознайомлення дітей з розв’язуванням задач розглядуваного виду [20, 28].
У методиці початкового навчання математики виділяють такі етапи розв'язування задач, як ознайомлення із змістом задачі, аналіз задачі і відшукання плану розв'язування, розв'язання задачі та перевірка розв'язування. Розглянемо методику роботи на кожному з цих етапів.
1. Ознайомлення із змістом задачі. Усвідомлення змісту задачі — необхідна умова її розв'язання. Учень не повинен приступати до розв'язування задачі, не зрозумівши її умови. Тому ознайомлення з задачею містить власне опанування її змісту і перевірки усвідомлення його дітьми.
Учень ознайомлюється з задачею із слів учителя або самостійно. Це, так би мовити, «крайні способи». Поряд з ними використовуються «проміжні способи», в яких ступінь самостійності учнів залежить від рівня їхньої підготовленості і мети розв'язування задачі. Приступаючи до розв'язування задачі, важливо сприйняти її в цілому, а потім вже розбивати на окремі частини [22, 26].
При фронтальному ознайомленні вчитель читає (або переказує) задачу двічі. Першого разу задачу читають з метою ознайомлення з її змістом в цілому. Другого разу задачу читають частинами і так, щоб кожна частина містила певну смислову «одиницю» тексту. Поділ задачі на частини здебільшого передбачає виділення окремих числових даних її. Під час другого читання доцільно на дошці записувати умову. Читаючи задачу, вчитель паузами та інтонацією виділяє числові дані та слова, що визначають вибір дії та запитання задачі. Емоційне забарвлення голосу допомагає учням уявити ту життєву ситуацію, про яку йдеться в задачі. Тому, слухаючи задачу, дітям не варто слідкувати очима за текстом підручника. Якщо в задачі є маловідомі дітям терміни, то їх слід пояснити заздалегідь, застосовуючи для цього предметне ілюстрування або малюнки.
Щоб перевірити, як учні усвідомили умову задачі, вчитель задає учням запитання (за смислом окремих частин) або пропонує переказати всю задачу. З метою активізації контрольного повторення задачі слід наперед ставити перед учнями те або інше завдання. Наприклад: «Послухайте задачу і повторіть вголос її запитання», «Прочитайте задачу самостійно і скажіть, що нам відомої про...». [7, 42]
Розглянуті вимоги стосуються і самостійного читання задач учнями. Діти повинні засвоїти, що в процесі, читання треба запам'ятати або виписати числові дані і виділити запитання задачі і найбільш важливі слова, які стосуються даних і шуканого чисел, а також з'ясувати незрозумілі слова.
2. Аналіз задачі і відшукання плану її розв'язування. Учень зможе успішно розв'язати задачу, якщо розумітиме значення слів і виразів, з яких вона побудована. На початку навчання і при розгляді нових задач усвідомлення значення слів та зв'язків між величинами досягається через відтворення тієї реальної проблемної ситуації, моделлю якої є задача. В подальшому дедалі частіше застосовується вербальний (словесний) аналіз (розбір) задачі.
Вербальний аналіз в широкому розумінні містить, з одного боку, семантичний аналіз, а з другого — знаходження способу розв'язування її. Суть семантичного аналізу полягає в тому, що на основі аналізу тексту задачі визначають окремі значення величин, а також відношення, що їх пов'язують. Таким аналізом передбачається:
а) поділ задачі на окремі частини, кожна з яких є словесним завданням певного елементу задачі;
б) визначення слів-ознак, що характеризують відношення між величинами, а отже й відповідну арифметичну дію [51, 35].
Під час аналізу треба з'ясувати, скільки величин розглядається в задачі та які вони мають значення. Задавання кожного значення величини звичайно складається з трьох частин: назви величини, зазначення особливості певного значення і числове значення, якщо воно відоме (задане). Якщо числове значення не задано, то воно є невідомим, і якщо, крім того, в завдання цього невідомого значення входить запитання «скільки»?» чи вимога «знайти», то це значення шукане.
Існують два способи розбору задачі: 1) від числових даних — до запитання; 2) від запитання — до числових даних. Перший спосіб часто називають аналітичним, а другий — синтетичним. Як в практичній роботі, так і в спеціальних дослідженнях не надається переваги тому чи іншому способу розбору задач. На нашу думку, в навчанні молодших школярів мають функціонувати обидва способи. Це важливо, бо спосіб розбору, який застосовує вчитель, є водночас зразком, прийомом самостійної роботи учнів у процесі розв'язування задач. Щоб навчити учнів користуватися цими способами розбору, необхідно спочатку їх пояснити, навести зразки, виконати розбір кількох задач (це можна доручити одному з учнів), а також зробити аналіз задач після їх розв'язання.
При самостійному розв'язуванні задач учні самі вибирають той спосіб розбору, який для них найзручніший. Проте слід підкреслювати, що в усіх випадках треба мати на увазі як числові дані, так і запитання задачі.
Вибір ілюстрації до задачі, повнота її розбору, ступінь самостійності учнів у розв'язуванні залежить від новизни і складності самої задачі. При цьому треба мати на увазі, що основна навчальна мета — розвинути в учнів уміння самостійно розв'язувати задачі — досягається тривалою практикою розв'язування задач як з використанням наочності, так і без неї. Отже, в застосуванні наочності треба дотримуватися певної міри [12, 91].
Мета використання ілюстрації — виявити величини, про які йдеться в задачі, та з'ясувати зв'язки між ними. Предметна ілюстрація допомагає створити уявлення про життєву ситуацію, описану в задачі, і тим самим сприяє правильному вибору дій та їх послідовності. Ілюстрація у вигляді короткого запису (схематичного, табличного) чи рисунка фіксує у зручній для сприймання формі величини (дані і шукані) допомагає розкрити залежності; між ними. У знаходженні неявної залежності між запитанням задачі і даними полягає інтерес дітей до процесу; розв'язування задач, а це, в свою чергу, сприяє їхньому розвитку мислення. Тому недоцільно намагатися якомога частіше розкривати зв'язки в задачах за допомогою короткого запису чи застосування іншої наочності.
Розв'язувати задачі з використанням короткого запису слід у таких випадках:
· при початковому розв'язуванні простих задач, коли цей процес є ще, по суті, переходом від операцій над і множинами предметів до арифметичних дій над натуральними числами;
· при розв'язуванні простих і складених задач з метою формування в учнів уявлення про структуру задачі;
· при використанні задач для формування математичних понять, ознайомлення учнів з елементами арифметичної теорії чи залежностями між величинами;
· при початковому ознайомленні учнів з задачею нового виду (і то не завжди), а також тоді, коли багато учнів не можуть самостійно розв'язати задачу [9, 213].
Учнів треба поступово привчати виконувати короткий запис задачі. У першому класі наслідують зразок учителя. Як самостійну роботу на уроці можна практикувати запис даних у задану схему. Вдома першокласники розв'язують задачу без короткого її запису. У 3-4 класах учитель дає не тільки зразки чи опорні схеми коротких записів, а й ознайомлює дітей з деякими рекомендаціями щодо їх виконання.
Наприклад:
У дівчинки було 5 книжок. Їй подарували ще кілька книжок. У неї стало 9 книжок. Скільки книжок подарували дівчинці?
Короткий запис:
Було – доданок – 5 книжок.
Подарували – доданок – ?
Стало – сума – 9 книжок.
Під час розв’язання учні міркують так: У цій задачі нам відомі сума і один доданок. Щоб визначити другий доданок (Скільки книжок подарували?), треба від суми відняти відомий доданок.
Віднімаємо: 9 – 5 = 4 (книжок).
Перевірка: віднімання перевіряємо дією додавання. Щоб перевірити, чи правильно ми розв’язали задачу, треба додати до відомого доданка той, що ми знайшли. Якщо одержимо відому суму, то задачу ми розв’язали правильно. Додаємо: 4 + 5 = 9 (книжок).
Отже, цю задачу ми розв’язали правильно, бо одержали відому суму.
Відповідь: дівчинці подарували 4 книжки.
Така організація навчання аж ніяк не переобтяжує пам’ять дітей, навпаки, вона полегшує формування умінь розв’язувати задачі, тому що кожен учень усвідомлює, чому цю задачу слід розв’язувати саме так.
Учні повинні знати, що в короткому записі треба використовувати слова, які визначають дію або залежність між даними і шуканою величинами. Зв'язані між собою дані слід записувати в одному рядку; число, яке є сумою кількох даних, записувати справа або зліва від них і відокремлювати рискою; запитання задачі позначати знаком запитання. У табличній формі два значення тієї самої величини треба записувати одне під одним [33, 45].
Умову задачі можна коротко записати в таблиці, або у формі креслення. Наприклад:
Задача 1. Зібрали 100 кг яблук, а груш на 20 кг більше, ніж яблук. Скільки кілограмів яблук і груш зібрали?
Груш – на 20 кг більше
Задача 2. Автомобіль використав за 4 год роботи 36 л бензину. Скільки літрів бензину потрібно для автомобіля на 8 годин роботи при тій самій нормі витрати за годину?
| Норма витрати бензину | Час роботи | Загальна витрата бензину |
| однакова | 4 год 8 год | 36 л ? |
3. Розв'язання задачі. Розв'язання задачі — це виконання арифметичних дій відповідно до складеного плану. Планом користуються і тоді, коли задачу розв'язують за допомогою складання виразу чи рівняння.
Виконуючи дії, учні коментують їх: що знайдено за допомогою кожної дії. При усному розв'язуванні задачі необов'язково щоразу називати питання плану повністю. Можна практикувати короткі коментарі.
Якщо задачу розв'язують письмово, то необхідні пояснення чи запитання учні можуть повідомляти усно або письмово. Обсяг письмових пояснень збільшується в міру оволодіння навичками письма. З різними формами пояснень учитель ознайомлює дітей поступово [24, 31].
Розв'язок задачі буває правильним і неправильним, точним і наближеним, загальним і частинним. Розв'язання кожної задачі повинно бути: 1) безпомилковим; 2) обгрунтованним; 3) повним; 4) раціональним.
4. Перевірка розв'язання та обґрунтування доведень є складовою частиною і характерною рисою математичної діяльності. Учням молодших класів ще важко відчувати потребу в обґрунтуванні своїх суджень. Тому перевірку розв'язання задачі вони сприймають лише як вимогу вчителя.
Перевірити розв'язання задачі — це з'ясувати, правильне воно чи ні. Для вчителя цей процес є засобом виявлення прогалин у знаннях учнів, а в поєднанні з аналізом та оцінкою — засобом виховання інтересу до вивчення математики. Проте така перевірка не вичерпує всієї проблеми. Треба поступово виховувати в дітей почуття необхідності самоперевірки, ознайомлювати їх із найбільш доступними прийомами перевірки. З цією метою слід проводити бесіди, в яких аналізувати допущені учнями помилки. Під час таких бесід розкривати особливість математики як науки, її роль у народному господарстві і в житті кожної людини, розповідати, як учені-математики та інші фахівці дбають про правильність результатів, аналізувати, до яких негативних наслідків можуть призвести допущені у розв'язанні задачі помилки [18, 19].
Що стосується сутності поняття “вміння розв’язувати текстові задачі”, його зв’язок із знаннями і навичками, то під вмінням розуміємо готовність і здатність учнів початкової школи самостійно і свідомо розв’язувати ці задачі. В процесі навчання математики доцільно виділяти окремі й узагальнені вміння. До окремих вмінь відносять вміння розв’язувати задачі певного виду. Якщо учень переносить засвоєні дії на нові види задач, правильно і самостійно розв’язує текстові задачі широкого кола, то відповідні вміння є узагальненими. Кінцевим результатом навчання є узагальнені вміння.
Загальне вміння розв’язувати текстову задачу утворює складний комплекс, що включає активне оперування математичними знаннями і відповідними вміннями й навичками, досвід у застосуванні знань і певну сукупність розумових дій, які необхідні для розв’язання [60, 47].
Вироблення вмінь учнів початкової школи розв’язувати текстові задачі передбачає ознайомлення їх із поняттям ”текстова задача” і процесом її розв’язування; ознайомлення учнів із структурними компонентами задачі (умова, вимога, дані відомі, невідомі, шукані), їх особливостями (умова і вимога зв’язані між собою; в умові має бути не менше двох числових даних, зв’язаних між собою і з шуканим; вимога виступає орієнтиром пошуку розв’язування; вибір дій відбувається шляхом встановлення взаємозв’язків між даними і шуканими та ін.).
У тісному зв’язку із знаннями предметом цілеспрямованого формування є вміння виділяти складові компоненти в тексті задачі, встановлювати повноту, обґрунтовувати правильність (неправильність) побудови текстової задачі, переформульовувати і самостійно їх складати.
На підставі визначених теоретичних основ нами удосконалена методика формування загального уміння розв’язувати складені задачі, в якій визначено мету і зміст кожного з зазначених етапів. На відміну від чинних підручників, ми пропонуємо проводити цілеспрямовану підготовку до введення поняття про складену задачу. На етапі підготовчої роботи засобом спеціальних завдань у дітей формуються уявлення: про те, що за двома певними числовими даними можна відповісти на кілька запитань; про те, що різні задачі можуть мати однакові розв’язання; про неможливість відповісти на запитання задачі, якщо числових даних бракує; про необхідність вибору числових даних для відповіді на запитання задачі; про існування задач, на запитання яких не можна відповісти одразу; про існування задач, що складаються з двох простих задач, які пов’язані за змістом; про те, що аналіз може складатися з двох циклів – кожний з яких відповідає певній з двох простих задач [23, 53].
Традиційно ознайомлення з поняттям “складена задача” здійснюється в 2-му класі на задачах на знаходження остачі, й ці задачі пропонуються учням майже протягом усієї теми. Але учні запам’ятовують спосіб розв’язування і при розв’язуванні нової задачі наслідують його, не звертаючись до розгорнених міркувань. Тому ознайомлення з поняттям “складена задача” та процесом її розв’язування проводиться на різноманітних математичних структурах задач. Такий підхід спонукає учнів до засвоєння дій з розв’язування задачі, а не до заучування плану розв’язування [35, 3].
Формування поняття про складену задачу та ознайомлення з процесом розв’язування складених задач здійснюється за допомогою порівняння задачі з двома запитаннями та відповідної складеної задачі; порівняння простої та складеної задач, які мають однакові умови; вибору необхідних і достатніх ознак для розпізнавання складеної задачі; підведення під поняття “складена задача”; виведення наслідків про належність або неналежність задачі до поняття “складена задача”. Спеціально опрацьовується уміння виконувати аналітичний пошук розв’язування задачі – спочатку до задач подаються готові схеми аналізу, потім – діти повинні самостійно заповнити схему аналізу на картці з друкованою основою, а далі складають її самі. Аналогічно формується вміння розбивати складену задачу на прості та визначати порядок розв’язування простих задач.
Істотним в організації діяльності учнів на етапі ознайомлення з поняттям “складена задача” (або “задача”) є її спрямованість не на розв’язання кожної конкретної задачі, а на оволодіння комплексом умінь, на оволодіння цим поняттям [49, 74].
Формування загального вміння розв’язувати складені задачі реалізується за допомогою систем навчальних задач для 2-го-4-го класів. Навчання розв’язувати складені задачі доцільно здійснювати на різноманітних математичних структурах задач, не зосереджуючись на відпрацюванні розв’язання задачі певної структури. Істотним у методиці ознайомлення із задачами нової математичної структури є введення їх на основі або порівняння зі схожими простими задачами, або на основі продовження сюжету простої задачі, або на основі зміни запитання простої задачі до даної умови, або на основі зміни умови або запитання складеної задачі відомої математичної структури.
Таким чином, досліджується вплив цих змін на розв’язування задачі; задачі нової математичної структури зіставляються з задачами вже відомими, що полегшує їх засвоєння. Крім того, застосовується й такий методичний прийом, коли задача нової структури подається без зіставлення з відомими структурами, що спонукає відтворення повного складу дій, які містить загальне уміння розв’язувати складені задачі.
При формуванні вміння розв’язувати складені задачі в 2-му – 4-му класах учням пропонуються складені задачі різноманітних математичних структур. У 3-му класі проводиться робота з узагальнення поняття “складена задача”, а також математичних структур складених задач на знаходження суми, різниці тощо, школярі вчаться складати обернені задачі; розпочинає формуватися дія синтетичного пошуку розв’язування задачі [18, 21].
На матеріалі задач з пропорційними величинами, на знаходження суми чи різницеве (кратне) порівняння двох добутків або часток основна увага приділяється опрацюванню дій визначення істотних ознак та узагальнення математичної структури і способу розв’язування задач. Дослідження задач відбувається за такими факторами: за зміною групи пропорційних величин; за зміною числових даних; за зміною шуканих задачі; за зміною співвідношень, що задані в задачі: сума значень величини замінюється їх різницевим, а потім й кратним співвідношенням; за зміною величин, для значень яких дано або треба знайти суму, різницеве чи кратне відношення; визначивши вплив цих змін на план розв’язування задач, ми виділяємо істотні ознаки математичних структур задач та узагальнюємо плани їх розв’язування [4, 41].
Усе це слід ураховувати, навчаючи дітей розв’язувати задачі. Один з істотних моментів цього навчання полягає в тому, щоб діти навчилися самостійно виконувати первинний аналіз тексту задачі, відділяючи відоме від невідомого. Важливо, щоб вони вміли не тільки вичленити із задачі числові дані, а й пояснити, що означає кожне з них у контексті, що сказано про те число, яке треба знайти, і т.д. Важливо, щоб у процесі первинного аналізу зверталася увага не лише на виділення даних і шуканого, а й на зв’язки між ними, викладені в тексті задачі.
РОЗДІЛ 2. МЕТОДИЧНА РОБОТА НАД ЗАДАЧАМИ НА ПРОПОРЦІЙНЕ ДІЛЕННЯ
Похожие работы
... робити схеми аналітичного або синтетичного способу розбору задач, хоча це не належить до обов'язкових умінь, наведених у програмі з математики для 1–4 класів. 2. Формування умінь учнів розв’язувати задачі на рух 2.1 Аналіз системи задач на рух у початковому курсі математики Вивчення всіх питань програми з математики пов'язане з розв'язуванням арифметичних задач. З одного боку, вони є ...
... школярів математичних уявлень і понять. Усвідомлення їх є важливим як для практично-життєвої підготовки учнів, так і для подальшого засвоєння математичних знань у середніх класах. 1.2 Проблема формування вмінь у другокласників розв’язувати складені задачі Традиційно ознайомлення з поняттям “складена задача” здійснюється в 2-му класі на задачах на знаходження остачі, й ці задачі пропонуються ...
... і дії і якості зі взірцем. 2. Характеристика дидактичних умов організації самостійної роботи у початкових класах та їх експериментальна перевірка 2.1 Організація самостійної роботи на уроці у початковій школі Самостійна робота на уроці – органічна частина навчального процесу. Тому методика її проведення визначається специфічними особливостями кожного предмета, змістом теми, рівнем пі ...
... –2007 навчальний рік) була визначена сфера і проблема дослідження; вивчалася педагогічна, методична література з даної теми; аналізувалася робота вчителів початкових класів у галузі методики розв’язування простих задач, що розкривають конкретний зміст арифметичних дій, шляхом диференційованого навчання; формулювалася гіпотеза та завдання дослідження. В процесі експериментального етапу (2007–2008 ...



0 комментариев