Олівців

48 олівців

Мал. 5.

Далі учні вчаться розв’язувати задачі на пропорційне ділення самостійно. Розглянемо таку задачу.

Задача. Дівчинка купила 3 зошити для себе і 2 зошити для однокласниці. За всі зошити вона заплатила 1 грн. Скільки грошей має віддати дівчинці однокласниця за зошити?

Задачу пропонують розв'язати самостійно, але перед цим слід з'ясувати, як знайти ціну одного зошита, що треба знати, щоб обчислити вартість покупки.

Розв'язування підготовчих задач активізує діяльність учнів при опрацюванні задач нового типу.

Розглянемо фрагмент уроку на тему "Ознайомлення із задачею на пропорційний поділ", де описана методика опрацювання таких задач.

Учням пропонують розв'язати задачу: "Купили 3 зошити в лінійку і 2 зошити в клітинку за тією самою ціною. За зошити в лінійку заплатили 54 коп. Скільки грошей заплатили за зошити в клітинку?" (за таблицею).

Ціна	Кількість	Вартість
Однакова	3 2	54 коп. ?

Діти розв'язують задачу окремими діями з поясненням у запитальній формі. У заздалегідь заготовлену таблицю на дошці вчитель записує суму вартостей всіх зошитів, знайдену учнями, і знаки запитання. Учні складають задачу на пропорційний поділ з двома запитаннями:

¾ Скільки грошей заплатили за зошити в лінійку?

¾ Скільки грошей заплатили за зошити в клітинку?".

Вчитель повідомляє, що ці два запитання можна замінити одним.

¾ Чи можна одразу дізнатися, скільки грошей заплатили за зошитив лінійку? (Ні).

—Що треба знати, щоб дізнатися, скільки грошей заплатили за зошити в лінійку? (Ціну зошита і кількість куплених зошитів у лінійку).

—Чи відома кількість зошитів у лінійку? (Відома).

—Чи відома ціна зошита в лінійку? (Невідома).

—Що сказано про ціну зошита в задачі? (Ціна зошита в лінійку і клітинку однакова).

—Чи можна дізнатися, скільки зошитів купили на 90 коп.? (Можна).Складіть план розв'язування задачі.

Далі учням пропонують розв'язати задачу на пропорційний поділ самостійно.

1. За 4 м шовку заплатили 80 грн. Яка ціна 1 м шовку?

80 : 4 = 20 (грн.)

2. У 6 банках 12 л вишневого соку. Скільки літрів соку в 1 банці?

12 □ 6 = □ (л).

1)В одному сувої 12 м сукна, а в другому - 8 м. Скільки метрів сукна у двох сувоях разом? (+).

2)В одному бідоні 10 л молока. Скільки літрів молока у 3 таких бідонах? (•).

Поступово вводяться задачі на пропорційне ділення з іншими трійками величин.

Задача. Двоє мулярів мурували будинок, одержуючи за робочий день однакову плату. Перший муляр працював 2 дні, а другий 3 дні. Скільки грошей одержав кожен муляр, якщо разом вони одержали 500 грн?

Після ознайомлення з умовою вчитель звертає увагу учнів на характер запитання:

— Про що треба дізнатися в задачі? (Скільки грошей одержав кожен муляр).

¾ Що означає вираз «кожен муляр»? (Це означає, скільки грошей одержав перший муляр і скільки другий).

¾ Отже треба знайти відповідь на два окремих запитання:

1) Скільки грошей одержав перший муляр?

2) Скільки грошей одержав другий муляр?

Далі учні розв'язують задачу самостійно, користуючись коротким записом умови.

Задачу учні розв'язують окремими діями. Підсумовуючи роботу, вчитель повторює весь хід міркування, властивий задачам на пропорційне ділення. Для узагальнення способу розв’язування задач на пропорційне ділення корисно практикувати вправи на перетворення задач. Наприклад, можна за задачею на знаходження четвертого пропорційного скласти задачу на пропорційне ділення. Такі вправи допоможуть дітям побачити схоже в способах розв’язування.

2.2 Формування умінь розв’язувати задачі на пропорційне ділення

У початкових класах учні розв'язують задачі майже на кожному уроці математики, міра навантаження при цьому різна. Для ознайомлення з новими видами задач здебільшого відводяться окремі уроки. Певна частина таких уроків планується також для розвитку вмінь учнів розв'язувати задачі. На уроках, присвячених вивченню нового арифметичного матеріалу чи застосуванню нових знань для розв'язання задач, відводиться в середньому 15-20 хвилин.

При розв'язуванні задачі нового виду учень повинен сприйняти її в цілому, застосувати певні знання чи прийоми обчислень в нових умовах, а також усвідомити нові функції об'єкта. Отже, розв'язування задач — це творчий процес. Враховуючи вимоги, які ставляться щодо проблемного навчання, вчитель має спрямовувати учнів на самостійне розв'язування задач за допомогою відповідних підготовчих вправ чи засобів унаочнення, своєчасно виявляти помилкові міркування в процесі розв'язування і подавати їм допомогу (але не послаблювати вольових зусиль), підтримувати емоційний тонус і впевненість у тому, що кожен з них спроможний самостійно розв'язати задачу.

У підвищенні активності учнів під час розв'язування задач важлива роль відводиться засобам контролю і самоконтролю. Під час ознайомлення та розбору задачі контрольними запитаннями можуть бути такі:

¾ Що відомо в задачі? Що невідомо?

¾ Що означає число, про яке йдеться в задачі?

¾ Чому не можна розв'язати задачу однією дією? Скільки дій треба виконати, щоб розв'язати задачу?

¾ Якого даного не вистачає щоб знайти відповідь на запитання задачі?

У процесі самостійної роботи (після розбору задачі або одразу після ознайомлення з нею) особливе значення має безпосереднє спостереження вчителя за роботою учнів, за їх записами в зошиті. Час, протягом якого учні записують розв'язання, треба повністю відводити для контролю і подання індивідуальної допомоги.

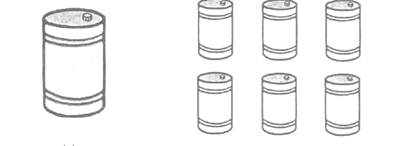
1. Розглянь малюнок і розв'язання задачі.

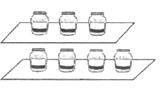
21 кг

¾ Скільки банок на верхній поличці? (3).

¾ Скільки банок на нижній поличці? (4).

¾ Скільки всього банок? (7).

¾ Яка маса варення в усіх банках? (21 кг).

¾ Як дізнатися, яка маса варення в одній банці? (Всю масу поділити на кількість банок з варенням).

Розв'язання.

1) 3+4 = 7 (б.) - всього банок з варенням;

2) 21 : 7 = 3 (кг) - маса варення в одній банці.

Відповідь: маса варення в 1 банці 3 кг.

2. Розглянь малюнки, склади задачі і запиши розв'язання.

1. Скільки важить одна упаковка з печивом?

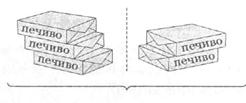
35 кг

2. Скільки олівців в одній коробці?

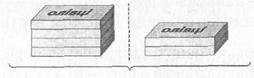
42 олівці

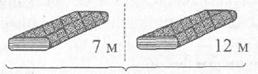
3. Яка ціна 1 метра тканини?

57 грн.

4. Яка ціна одного м'яча?

35 грн.

5. Купили два відрізи однакової тканини. У першому відрізі було 4м, а в другому – 5 м. За обидва відрізи заплатили 72 грн. Скільки грошей заплатили за кожний відріз?

 І - 4 м - ? 72 грн

 ІІ – 5 м - ?

¾ Про що запитується в задачі? (Скільки грошей заплатили за кожний відріз).

¾ Що означає вираз «кожний відріз»? (Це означає, що треба дізнатися, скільки грошей заплатили за перший відріз і скільки за другий).

¾ Отже, треба знайти відповіді на два окремих запитання:

¾ Скільки грошей заплатили за перший відріз?

¾ Скільки грошей заплатили за другий відріз?

¾ Що треба знати, щоб відповісти на ці запитання? (Треба знати ціну одного метра тканини).

¾ Як дізнатися про ціну 1 метра тканини? (Треба вартість усієї тканини поділити на кількість метрів у двох відрізах).

Розглянь розв'язання.

1) Скільки метрів тканини у двох відрізах?

5 + 4 = 9 (м)

2) Яка ціна одного метра тканини?

72 : 9 = 8 (грн.)

3) Скільки грошей заплатили за перший відріз?

8 . 4 - 32 (грн.)

4) Скільки грошей заплатили за другий відріз?

8 - 5 = 40 (грн.)

Відповідь: 32 гривні і 40 гривень.

Перевірка: 32 + 40 = 72 (грн.).

Складаємо вирази: 72 : (5 + 4) • 4 = 32.

72 : (5 + 4) • 5 - 40.

6. Два однакові автомобілі перевезли 119 т вантажу. Перший автомобіль зробив 9 рейсів, а другий - 8. Скільки тонн вантажу перевіз кожний автомобіль?

І – 9 р. - ? 119 т

ІІ – 8 р. - ?

Користуючись зразком, дай відповіді на запитання:

¾  Про що запитується в задачі?

¾  Що означає вираз «кожний автомобіль»?

¾  Отже, на які два окремих запитання треба дати відповіді?

¾ Що треба знати, щоб відповісти на запитання задачі?

¾  Як дізнатися, скільки тонн вантажу перевозить автомобіль за один рейс?

¾  Склади план і запиши розв'язання задачі.

¾  9 + □ = □ (р.) - усього рейсів;

¾  119 : □ = □ (т) - перевозить 1 автомобіль за 1 рейс;

¾  □ • □ = □ (т) - перевіз перший автомобіль;

¾  □ • □ = □ (т) - перевіз другий автомобіль.

Відповідь: 63 т вантажу, 56 т вантажу.

Склади вирази: 119 : (9 + □) • □ = □;

119: (9 + □)•□ = □.

7. З першої ділянки накопали 7 мішків картоплі, а з другої - 8 таких самих мішків картоплі. Всього накопали 750 кг картоплі. Скільки кілограмів картоплі накопали з кожної ділянки?

¾ Про що йдеться в задачі? (Про картоплю, яку накопали з двох ділянок).

¾ Скільки мішків картоплі накопали з першої ділянки? (7).

¾ Скільки мішків картоплі накопали з другої ділянки? (8).

¾ Скільки кілограмів картоплі накопали з двох ділянок? (750 кг).

¾ Про що запитується в задачі? (Скільки кілограмів картоплі накопали з кожної ділянки).

¾ Міркуй далі сам.

¾ Запиши розв'язання задачі і поясни, про що дізналися у кожній дії.

1)□ + □ = □ (м.);

1)□ : □ = □ (кг);

2)□ • □ = □ (кг);

3)□ • □ = П (кг).

Відповідь: 350 кг картоплі, 400 кг картоплі.

¾ Склади вирази: 750 : (□ + □)-□ = 350;

750 :(□ + □)•□ = 400.

8. Пасажирський літак за 2 рейси пролетів 3360 км. Перший рейс він пролетів за 4 год, а другий - за 3 год. Яка довжина кожного рейсу, якщо літак увесь час летів з однаковою швидкістю?

 І – 4 год - ? 3360 км

ІІ – 3 год - ?

Розв'яжи задачу за даним планом.

1)Скільки часу літак був у польоті?

2)Яка швидкість літака?

3)Яку відстань пролетів літак за 4 год?

4)Яку відстань пролетів літак за 3 год?

Відповідь: 1920 км, 1440 км.

Склади вирази: □ : (□ + □)- 4 = 1920;

(□ + □). 4 = 1440.

9. Першого разу на склад завезли 2 вагони бурого вугілля, а другого - 4 таких самих вагони. Всього завезли 96 т. Скільки тонн вугілля завезли кожного разу?

Вказівка. Це задача на три дії.

У першій дії дізнайся, скільки всього було вагонів з вугіллям.

У другій дії дізнайся про масу вугілля в одному вагоні.

Відповідь: 32 т вугілля, 64 т вугілля.

10. На одну підводу поклали 4 мішки жита, а на другу - 3 таких мішки. У мішках було 420 кг жита. Скільки кілограмів жита поклали на кожну підводу? Відповідь: 240 кг жита, 180 кг жита.

11. Петрик купив 2 альбоми, а Івасик - 3 таких альбоми. За всі альбоми вони заплатили 10 грн. Скільки грошей заплатив за альбоми Петрик, а скільки - Івасик?

Відповідь: 4 гривні, 6 гривень.

12. Добери числові дані і розв'яжи задачу.

В одній пачці було □ зошитів, а в другій - □. За всі зошити заплатили □ грн. Скільки окремо грошей заплатили за кожну пачку зошитів?

13. Господиня купила 3 кг яблук для себе і 2 кг для сусідки. За всі яблука господиня заплатила 10 грн. Скільки грошей має віддати сусідка господині?

Відповідь: 4 гривні.

14. Постав запитання і розв'яжи задачу.

Дві групи дітей збирали жолуді. Перша група зібрала 3 мішки жолудів, а друга - 4 таких мішки. Всього діти зібрали 280 кг жолудів. Скільки... ?

Відповідь: 120 кг жолудів, 160 кг жолудів.

15. Відшукай зайві дані і розв'яжи задачу.

За перший день швачка пошила 3 однакових плаття, а за другий день – 2 таких плаття. На всю роботу вона витратила 15 м тканини. На третій день закупили ще 20 м тканини. Скільки метрів тканини витрачала швачка кожного дня?

Відповідь: 9м тканини, 6 м тканини.

Перевірка: □ + □ = □.

16. Склади задачу про однакові ящики з помідорами за коротким записом.

І – 4 ящ. - ? 105 кг

 ІІ – 3 ящ. - ?

Відповідь: 60 кг помідорів, 45 кг помідорів.

17. Склади подібну задачу про дві машини з мішками пшениці.

18. Запиши розв'язання задачі.

Дві бригади зібрали 5 корзин моркви. Перша бригада зібрала 36 кг, а друга - 24 кг. Скільки корзин моркви зібрала кожна бригада?

І – 36 кг - ? 5 корзин

ІІ – 24 кг - ?

1 (+); 2 (:); 3 (:); 4 (:).

Відповідь: 3 корзини моркви, 2 корзини моркви. Перевірка: 3 + 2 = 5.

19. З двох ділянок зібрали 15 мішків картоплі. З першої зібрали 350 кг картоплі, а з другої - 400 кг. Скільки мішків картоплі зібрали з кожної ділянки?

І – 350 кг - ? 15 мішків

ІІ – 400 кг - ?

Відповідь: 7 мішків картоплі, 8 мішків картоплі.

20. Два однакові автомобілі зробили 17 рейсів. Перший автомобіль перевіз 63 т вантажу, а другий - 56 т. Скільки рейсів зробив кожний автомобіль?

Відповідь: 9 рейсів, 8 рейсів.

21. 20 л молока розлили у 4 каструлі і 6 банок. Місткість каструлі і банки однакова. Скільки літрів молока було в банках?

Зміни запитання задачі так, щоб задача розв'язувалася на 4 дії.

Відповідь зміненої задачі: 8 л молока і 12 л молока.

22. Добери умову подібної задачі до запитання:

Скільки літрів бензину заправили в кожний автомобіль?

23. Знайди помилку у розв'язанні задачі і розв'яжи правильно.

Бензин був у 3 каністрах. У перший автомобіль заправили 40 л бензину, а в другий - 20 л. Скільки каністр бензину було заправлено в кожний автомобіль?

Розв'язання.

40 + 20 = 60 (л) - всього бензину;

60 : 3 = 20 (л) - в одній каністрі;

20 : 20 = 1 (к.) - в перший автомобіль;

3 + 1 = 4 (к.) - в другий автомобіль.

Відповідь: □ к. і □ к.

24. Склади задачу за коротким записом і розв'яжи її.

	Кількість вагонів	Маса
І потяг II потяг	? 16 вагонів ?	540 т 420 т

Відповідь: 9 вагонів і 7 вагонів.

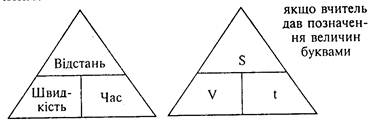
Розглянемо задачі на пропорційне ділення з трійкою величин «швидкість», «час», «відстань».

Задача. Автотуристи першого дня проїхали 360 км, другого — 240 км. На весь шлях затратили 10 год. Скільки годин були в дорозі туристи щодня, якщо вони їхали з однаковою швидкістю?

Швидкість	Час		Відстань
Однакова	? ?	10 год	360 км 240 км

На дошці подано план розв'язання задачі.

1)Скільки кілометрів проїхали автотуристи за 10 год?

2)Скільки кілометрів за годину проїжджали автотуристи?

3)Скільки годин були в дорозі туристи першого дня?

4)Скільки годин були в дорозі туристи другого дня?

— До кожного запитання плану розв'язання задачі виберіть дію.

Розв'яжіть задачу окремими діями без письмового пояснення і запишіть скорочену відповідь. Поясніть розв'язання задачі.

—До першого запитання задачі виберемо дію додавання. Якщо першого дня автотуристи проїхали 360 км, а другого—240 км, то за 10 год вони проїхали число кілометрів, що дорівнює сумі чисел 360 і 240. Буде 600. За 10 год автотуристи проїхали 600 км. Щоб дати відповідь на друге запитання, треба виконати дію ділення. Щоб знайти швидкість, треба відстань поділити на час. 600 поділити на 10, буде 60. Автотуристи проїжджали 60 км/год.

До третього запитання плану задачі треба вибрати дію ділення. Щоб знайти час руху автотуристі в першого дня, треба відстань поділити на швидкість. Першого дня вони проїхали 360 км зі швидкістю 60 км/год. 360 поділити на 60, буде 6. Першого дня автотуристи були в дорозі 6 год. Щоб дати відповідь на четверте запитання задачі, треба виконати дію ділення. Щоб знайти час, треба відстань поділити на швидкість. Другого дня туристи проїхали 240 км зі швидкістю 60 км/год. 240 поділити на 60, бу- де 4. Другого дня автотуристи були в дорозі 4 год.

Розглянемо задачі на пропорційне ділення з іншою трійкою величин.

Задача. Два робітники працювали однакову кількість днів і відремонтували 80 двигунів. Один робітник ремонтував за день 6 двигунів, а другий — 4. Скільки двигунів відремонтував кожен робітник?

Продуктивність праці	Кількість днів	Загальна кількість двигунів
6 дв. 4 дв.	Однакова	? ?	80 дв.

На дошці записано розв'язання задачі.

1) 6+4=10;

2) 80:10 = 8;

3) 6•8=48;

4) 4•8 = 32.

Відповідь

— Про що дізнавалися кожною дією?

—У першій дії дізналися про число двигунів, які відремонтували обидва робітники за день. їх число дорівнює сумі чисел 6 і 4. Буде 10.10 двигунів відремонтували обидва робітники за день. У другій дії дізналися про кількість днів, протягом яких ремонтували робітники 80 двигунів. За один день робітники ремонтували 10 двигунів і відремонтували 80 двигунів. Треба дізнатися, скільки разів число 10 вміщується в числі 80. 80 поділити на 10, буде 8.8 днів ремонтували робітники двигуни. Якщо перший робітник за день ремонтував 6 двигунів, то за 8 днів він відремонтував у 8 разів більше. Треба 6 помножити на 8, буде 48. Перший робітник відремонтував 48 двигунів. Якщо другий робітник за годину ремонтував 4 двигуни, то за 8 днів він відремонтує у 8 разів більше. Треба 4 помножити на 8, буде 32. Другий робітник відремонтував 32 двигуни.

Розглянемо задачі на пропорційне ділення з іншою трійкою величин.

Задача 1. Кондитерська фабрика випекла за перший день 640 кг печива, а за другий — 960 кг такого самого печива. Готове печиво розклали в 200 однакових ящиків. Скільки ящиків печива випекла фабрика першого і другого дня окремо?

У комплексній змінній таблиці подано скорочений запис розв'язання задачі.

Маса печива в одному ящику	Кількість ящиків		Загальна маса печива
Однакова	? ?	200 ящ.	640 кг 960 кг

1)Складіть план розв'язання задачі.

2)Скільки кілограмів печива випекла фабрика за 2 дні? Скільки кілограмів печива в одному ящику? Скільки ящиків печива випекла фабрика першого дня? Скільки ящиків печива випекла фабрика другого дня?

3)Розв'яжіть задачу, записавши окремі дії. Запишіть скорочену відповідь задачі.

—Прочитайте відповідь задачі.

Задача 2. Потяг везе 1000 т вантажу. В ньому однакова кількість сорокатонних і шістдесятитонних вагонів. Скільки сорокатонних і шістдесятитонних вагонів окремо було в потязі?

У комплексній змінній таблиці подано скорочений запис задачі, на дошці записано початок її розв'язання.

Вантажність вагона	Кількість вагонів	Загальна маса
40 т 60 т	Однакова	? ?	200 ящ.

Запис на дошці

1)40 + 60=100; 2)1000:100 = ...;

3)……………….. ;

4)………………… .

Відповідь.

— Запишіть розв'язання задачі. Поясніть її розв'язання.

Задача 3. З однієї грядки зібрали 16 однакових мішків картоплі, а з другої—4 таких мішки. Маса всієї зібраної картоплі 650 кг. Скільки кілограмів картоплі зібрали з кожної грядки окремо?

У комплексній змінній таблиці подано скорочений запис задачі.

Маса картоплі в мішку	Кількість мішків	Загальна маса
Однакова	6 м 4 м	? ?	650 кг

На дошці записано вирази: 650: (6 + 4) • 6; 650: (6 + 4) • 4.

— Поясніть, чому ці вирази є розв'язком задачі.

—Якщо з однієї грядки зібрали 6 мішків картоплі, з другої — 4 таких мішків, то число всіх мішків картоплі дорівнює сумі чисел 6 і 4.3 умови задачі відомо, що всього зібрали 650 кг.

Якщо 650 поділити на число всіх мішків картоплі, то знайдемо масу картоплі в одному мішку. Частка від ділення числа 650 на суму чисел 6 і 4 — це маса картоплі в одному мішку.

Помноживши частку числа 650 на суму чисел 6 і 4 на число мішків зібраних з першої грядки, знайдемо масу картоплі, зібраної з першої грядки. Якщо помножити вираз 650 : (6 + 4) на 4, то знайдемо, скільки кілограмів картоплі зібрали з другої грядки.

Задача 4. За перший день у магазин завезли 540 м тканини, а за другий — 460 м такої тканини. Всього в магазин завезли 50 сувоїв тканини.

Скільки сувоїв тканини завезли кожного дня в магазин?

У комплексній змінній таблиці подано скорочений запис задачі.

Довжина тканини в сувої	Кількість сувоїв	Загальна довжина
Однакова	? сувоїв 50 сувоїв ? сувоїв	540 м 460 м

— Користуючись схемою, поясніть, як знайти, скільки сувоїв тканини завезли в перший магазин (в другий магазин).

Значна увага звертається на розв’язування учнями задач на пропорційне ділення ІІІ виду.

Задача. Костюм для дорослого коштує 220 грн., а для дитини — 80 грн. Магазин продав однакову кількість костюмів для дорослих і дітей на суму 2 400 грн. Скільки гривень коштували костюми для дорослих і дітей окремо?

У комплексній змінній таблиці подано скорочений запис задачі.

Ціна	Кількість	Вартість
220 м 80 м	Однакова	? грн. 2400 грн ? грн.

— Користуючись схемою, розв'яжіть задачу окремим діями без письмового пояснення. Запишіть скорочену відповідь. Прочитайте розв'язання.

Також значна увага звертається на самостійне розв’язування задач учнями.

— Складіть і розв'яжіть задачу за скороченим записом.

Маса картоплі в мішку	Кількість	Маса посилки		Кількість
Посилка з фруктами Посилка з книжкамиа	Однакова	? ?	7 кг	30 кг 40 кг

Також доцільно при розв’язуванні задач на пропорційне ділення використовувати прийом диференційованого підходу — урізноманітнення вимог до розв'язання задачі на пропорційне ділення, тобто скласти вирази, які будуть розв'язком задачі.

У початкових класах рівень уміння учнів розв'язувати задачі є визначальним для характеристики стану засвоєння математики в цілому. Основні методи перевірки — це усне опитування і письмові роботи учнів. Опитування, в свою чергу, включає: усне розв'язування простих і складених задач, розв'язування задач із записами на дошці чи на окремих аркушах, пояснення розв'язань задач, різні види творчої роботи над задачею (порівняння, складання задач тощо).