Навигация
Развитие способностей к математическому творчеству
4. Развитие способностей к математическому творчеству.
Развитие творческих способностей – это необходимый элемент современного урока математики. Воспитанию стремления к творчеству следует уделять пристальное внимание на всех этапах обучения. Каждый предмет школьного курса способен внести свою долю воздействия на творческий облик учащегося. Математика представляет для этого исключительные возможности.
Способности к математическому творчеству, и конечно творчеству вообще, развиваются в результате:
ü поиска решения нестандартных задач;
ü решения задач и упражнений, включающих элементы исследования;
ü решения задач на доказательство;
ü решения задач и упражнений в отыскании ошибок;
ü решения занимательных задач;
ü в отыскании различных вариантов решения одной задачи и выбора лучшего из них;
ü при решении задач, в которых применяются сведения из всех математических дисциплин (комбинированных задач);
ü при решении синтетических задач.
Важно и то, что от степени творческой активности учащихся зависит эффективность учебной деятельности по развитию мышления.
Подробнее о развитии способностей к математическому творчеству можно найти в статье Канина Е.С. «Некоторые вопросы психологии обучения решению математических задач» ([24]).
Итак, основные идеи современного урока, требования к современному уроку на уроке математики в опыте работы учителей находят свое отражение.
§2. Реализация требований к современному уроку в личном опыте преподавания математики. 2.1 Подготовка к проведению эксперимента.Мною была проведена опытно-экспериментальная работа, целью которой было: выяснить повышает ли качество математического обучения соблюдение современных требований к современному уроку.
Эксперимент проводился в школе № 27 г. Кирова, в 10 “б” физико-математическом классе. Обучение в данном классе велось по учебнику Алимова М. А. «Алгебра и начала анализа 10-11».
Для достижения цели опытно-экспериментальной работы было проведено диагностирование обученности учащихся класса. Диагностирование обученности – это контроль и оценка знаний и умений обучаемых.
Приведем методику определения уровня обученности по П.И. Третьякову [74].
Обученность – это уровень реально усвоенных знаний, умений и навыков.
Существует пять уровней обученности.
Первый уровень обученности – различение. Он характеризуется тем, что ученик может отличить объект, процесс по наиболее существенным признакам от их аналогов.
Второй уровень обученности – запоминание. При этой степени обученности ученик может пересказать содержание текста, правила, положения, теоретические утверждения, но это не является доказательством его понимания, т. е. это только воспроизведение.
Третий уровень обученности – понимание. Ученик может находить существенные признаки и связи предметов и явлений, вычленять их из несущественных на основе анализа и синтеза; применять правила логического умозаключения, устанавливать сходства и различия.
Четвертый уровень обученности – умений и навыков.
Это наиболее высокий уровень обученности. Умения – закрепленные на практике способы применения знаний. Навык – умение, доведенное до автоматизма. Этот уровень обученности характеризуется умением применять на практике полученные теоретические знания, решать задачи с использованием усвоенных законов и правил.
Пятый уровень обученности – перенос знаний, умений и навыков в новую ситуацию. Обладающие этой степенью обученности умеют обобщать, применять полученные знания в новой ситуации.
Для определения обученности обычно используют самостоятельные работы, составленные в соответствии с уровнями обученности. Приведем ключевые слова для заданий самостоятельной работы по определению уровня обученности:
I уровень - различение: сравни, выбери, сопоставь, найди лишнее…
II уровень - воспроизведение: воспроизведи, нарисуй, напиши, перескажи товарищу…
III уровень – понимание: отчего, почему, зачем, в связи с чем, установи причинно-следственные связи, что может быть общего, выдели единичное, обобщи…
IV уровень – умений и навыков: выполни по образцу, по правилу, по формуле, перескажи, сопоставляя что-то с чем-то, какая закономерность, какие свойства…
V уровень – перенос: сочини, придумай, спроектируй, смоделируй, докажи, разыграй, выведи…
![]()
Диагностирование обученности включало в себя предварительный контроль, текущий контроль и итоговый контроль.
Предварительный контроль проводился с целью фиксации исходного уровня обученности (реально усвоенные знания, умения, навыки) и осуществлялся с помощью специально организованной самостоятельной работы по определению уровня обученности.
Текущий контроль необходим для диагностирования хода дидактического процесса, выявления динамики последнего; осуществлялся с помощью отслеживания итогов самостоятельных работ.
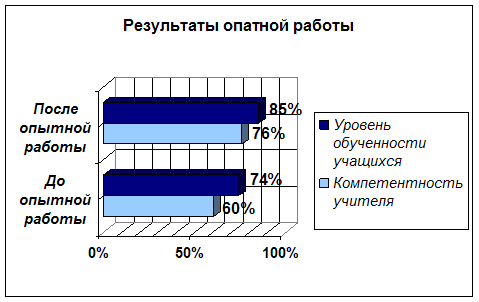
Итоговый контроль проводился с целью фиксации конечного уровня обученности и осуществлялся с помощью специально организованной самостоятельной работы по определению уровня обученности.
Сравнение исходного уровня обученности с конечным уровнем обученности позволяет судить об эффективности дидактического процесса и в итоге о повышении или понижении качества математического образования.
На момент проведения эксперимента класс изучил тему «Показательная функция, ее свойства и график». На эту тему и была организована самостоятельная работа диагностического характера, для определения исходного уровня обученности.
Предварительный контроль. Самостоятельная работа на тему «Показательная функция, ее свойства и график» (см. Приложение № 1).
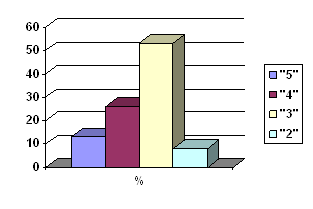
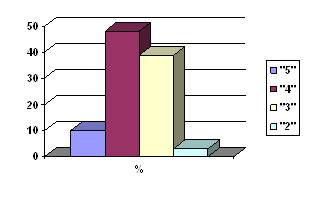
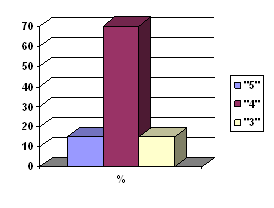
Результаты предварительного контроля (см. Приложение № 2).
2.2. О проведенных современных уроках.Далее, было запланировано 4 урока алгебры и начал анализа, на которых были осуществлены попытки реализации требований к современному уроку на практике:
1 урок. Показательные уравнения. Технология: проблемное обучение.
2 урок. Показательные уравнения. Технология: групповое обучение.
3 урок. Показательные неравенства. Технология: модульное обучение.
4 урок. Показательные неравенства. Технология: модульное обучение.
Сейчас о каждом уроке более подробно.
1 УРОК
Первый урок проводился по технологии проблемного обучения. Немного об этой технологии.
Проблемное обучение – это обучение, при котором преподаватель, систематически создавая проблемные ситуации и организуя деятельность учащихся по решению учебных проблем, обеспечивает оптимальное сочетание их самостоятельной поисковой деятельности с усвоением готовых выводов науки.
Проблемное обучение направлено на формирование познавательной самостоятельности учащихся, развитие их логического, рационального, критического и творческого мышления и познавательных способностей.
Проблемная ситуация – это состояние умственного затруднения, вызванного в определенной учебной ситуации объективной недостаточностью ранее усвоенных учащимися знаний и способов умственной или практической деятельности для решения возникшей познавательной задачи.
В процессе обучения математике существуют разные возможности создания проблемных ситуаций ([60],[75]).
Можно выделить практические этапы деятельности учащихся при использовании технологии проблемного обучения. На первом этапе происходит осознание проблемы, учащиеся вскрывают противоречие, заложенное в вопросе. Это противоречие может быть разрешено с помощью гипотезы. Формулирование гипотезы составляет второй этап. Третий этап решения проблемы доказательство гипотезы. Заканчивается решение проблемы общим выводом, в котором изучаемые причинно-следственные связи углубляются и раскрываются новые стороны познаваемого объекта или явления – четвертый этап решения проблемы [38].
Урок по теме «Показательные уравнения» (см. Приложение № 3).
Приведем замечание по проведенному уроку. В практической реализации урока при общих выводах по решенной проблеме желательно было бы провести с учащимися некоторую (хотя еще не совсем полную) классификацию показательных уравнений и способов их решения. Один из вариантов классификации показательных уравнений можно найти в [5] (там же много и практических заданий). Приведем классификацию показательных уравнений применительно к проведенному уроку.
Классификация показательных уравнений.
![]()
I тип. Простейшие показательные уравнения.
![]()
II тип. Показательные уравнения, приводящиеся к виду:
![]()
где ![]() - некоторые функции зависящие от
- некоторые функции зависящие от ![]() (одна из них может быть константой).
(одна из них может быть константой).
III тип. Показательные уравнения вида:
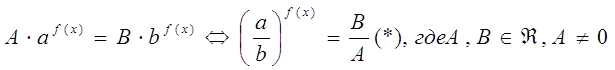
Уравнение (*) приводится к уравнению типа II или может не иметь решений, если ![]() .
.
IV тип. Показательные уравнения вида:
![]()
(отличительная особенность: наличие одного и того же коэффициента перед ![]() ), где
), где ![]() и
и ![]() - постоянные величины. Для решения этого уравнения вынесем за скобки общий множитель
- постоянные величины. Для решения этого уравнения вынесем за скобки общий множитель ![]() , где
, где ![]() , наименьшее из чисел
, наименьшее из чисел ![]() . После этого уравнение примет вид
. После этого уравнение примет вид
![]()
Выражение стоящее в скобках уравнения (1) является постоянной величиной. Обозначим эту величину буквой ![]() , тогда уравнение (1) примет вид
, тогда уравнение (1) примет вид
![]() , откуда имеем при
, откуда имеем при ![]()
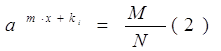
Уравнение (2) является уравнением типа III.
V тип. Показательные уравнения вида:
![]()
С помощью подстановки ![]() приводятся к квадратному уравнению
приводятся к квадратному уравнению ![]() . Решив последнее, найдем его корни
. Решив последнее, найдем его корни ![]() и
и ![]() . После этого уравнение (*) сводится к решению следующих двух показательных уравнений
. После этого уравнение (*) сводится к решению следующих двух показательных уравнений ![]() и
и ![]() . Эти уравнения приводятся к I типу.
. Эти уравнения приводятся к I типу.
В психологии считается, что разбиение рассматриваемых объектов на виды, типы (т.е. их классификация) сохраняется в памяти намного дольше и воспринимается более осознано, чем рассмотрение отдельных объектов. Поэтому классификация показательных уравнений поможет учащимся запомнить виды уравнений и способы их решения. В дальнейшем эта классификация может быть дополнена новыми видами уравнений.
Похожие работы
... уроки сказки, веселые задачи в стихах, математические загадки, сказочные задачи, математические сказки, задачи занимательного характера, головоломки, кроссворды и логические задачи способствуют активизации мыслительной деятельности учащихся на уроках математики, подтвердилась. Для себя лично я усвоила правило: "Не бери игру на урок, для того чтобы развлечься. Все на уроке должно быть логически ...
... одна из ее сторон – урок. В работе доказано, что самоанализ урока является основой эффективного управления процессом обучения. Дальнейшей же перспективой исследования является рассмотрение самоанализа всей деятельности учителя как основы управления процессом обучения математике. Изложенное выше позволяет считать, что самоанализ урока математики позволяет управлять процессом обучения школьников и ...
... оказывают положительное воздействие на развитие памяти и мышления, воспитания воли, привычки к систематическому учебному труду и самоконтролю, повышение ответственности за выполняемую работу. Комплексное использование всех возможностей контроля и оценки успеваемости учащихся, в конечном счете, направлено на обеспечение высокого качества процесса обучения и подготовки учащихся. Теорией и ...
... , развивающая логическое и системное мышление, в свою очередь занимает достойное место в истории, помогая лучше ее понять. Как, решая проблему формирования интереса учеников к учению, использовать возможности двух школьных предметов? Сведения из истории математики, задачи исторического характера, софизмы - лишь немногие "точки соприкосновения" этих, казалось бы, далеких, но достаточно близких наук ...

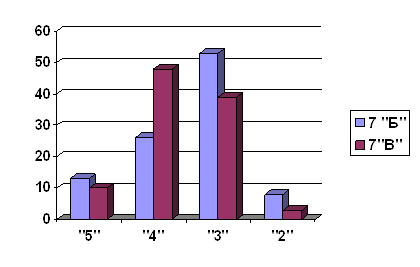
0 комментариев