Реализация на уроке в оптимальном соотношении всех дидактических принципов и правил из них вытекающих
Современный урок математики характеризуется усилением функции управления процессом формирования новых знаний
Развитие способностей к математическому творчеству
УРОК
Из указанных функций выберите те, которые являются показательными функциями. Выпишите их номера
Прочитайте теорию (см. ниже). Занесите в тетрадь ту информацию, которую считаете нужной
Решите неравенство (решение полностью обоснуйте)
Навигация
Прочитайте теорию (см. ниже). Занесите в тетрадь ту информацию, которую считаете нужной
Современный урок математики, требования к нему
124663
знака
4
таблицы
8
изображений
1. Прочитайте теорию (см. ниже). Занесите в тетрадь ту информацию, которую считаете нужной.
Теория.
Рассмотрим решение показательных неравенств вида 
Где 
и 
некоторые функции зависящие от 
.
Частным случаем неравенств вида являются неравенства вида 
, где 
– некоторое действительное число.
Для решения неравенств рассмотренных видов используется свойство возрастания или убывания показательной функции.
Решим неравенство (*).
Рассмотрим показательную функцию
. И рассмотрим значения показательной функции при t1=f(x) и при t2=g(x). Перепишем данное неравенство (*) в виде 
(**).
Если 
, то функция возрастает. Тогда неравенство (**) равносильно неравенству 
. А данное неравенство (*) неравенству 
.
Если 
, то функция убывает. Тогда неравенство (**) равносильно неравенству 
. А данное неравенство (*) неравенству 
.
Рассмотрите приведенные ниже примеры решения показательных неравенств вида .
Пример 1. Решите неравенство 
Запишем неравенство в виде 
. Показательная функция 
возрастает 
. Поэтому данное неравенство равносильно неравенству 
. Откуда 
. Решив квадратное неравенство, получим 
. Ответ: 
.
Пример 2. Решите неравенство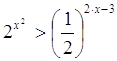 
Запишем неравенство в виде 
. Показательная функция 
возрастает 
. Поэтому данное неравенство равносильно неравенству
, откуда 
. Решив квадратное неравенство, получим 
или 
.
Ответ: 
.
2. Решите неравенства. Дайте полное обоснование решения неравенств (см. примеры).
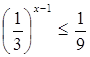
Проконтролируйте верность своего решения у соседа по парте.
Учебный элемент №3.
1. Решение некоторых показательных неравенств сводится к решению квадратных неравенств. Рассмотрите пример такого показательного неравенства.
Пример. Решим неравенство 
Пусть 
, тогда получим квадратное неравенство 
.
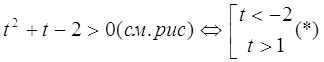
Так как 
, то получим, что совокупность
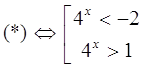
Первое неравенство не имеет решений, так как 
при всех 
. Второе неравенство можно записать в виде 
, откуда 
.
Ответ:
.
2. Решите неравенство 
. Проконтролируйте правильность решения самостоятельно.
Выполните самостоятельную работу в тетраде. Не забывайте обосновывать свои решения.
Самостоятельная работа.
Вариант №1.
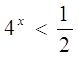
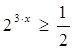
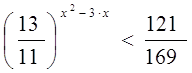
Вариант №2.
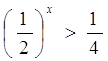
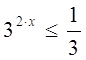
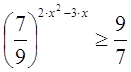
Оцените свою работу на уроке по 10 бальной шкале (поставьте свою точку на шкале).
Приложение № 6.
Итоговый контроль. Самостоятельная работа на тему «Показательные уравнения и неравенства».
В – 1.
1. Каждому уравнению и неравенству сопоставьте решение:
(1) 
(2) 
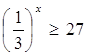
(3) 
(4) 
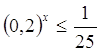
(5) 
(6) 
(7) 
(8) 
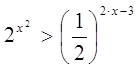
Решения: 1) 
, 2) -1, 3) 
, 4) 
, 5)уравнение решений не имеет,
6) 
, 7) 
, 8) 
, 9) неравенство решений не имеет, 10) 0, 11) 2,
12) 
, 13) 3, 14) 
, 15) 4, 16) 
, 17) 
.
2. 1) Продолжите: Показательным уравнением называется уравнение…,
2) Какое свойство показательной функции используется при решении неравенств? Сформулируйте его.
3. График функции 
расположен ниже графика функции 
при 
. Объясните почему.
Похожие работы
... уроки сказки, веселые задачи в стихах, математические загадки, сказочные задачи, математические сказки, задачи занимательного характера, головоломки, кроссворды и логические задачи способствуют активизации мыслительной деятельности учащихся на уроках математики, подтвердилась. Для себя лично я усвоила правило: "Не бери игру на урок, для того чтобы развлечься. Все на уроке должно быть логически ...
... одна из ее сторон – урок. В работе доказано, что самоанализ урока является основой эффективного управления процессом обучения. Дальнейшей же перспективой исследования является рассмотрение самоанализа всей деятельности учителя как основы управления процессом обучения математике. Изложенное выше позволяет считать, что самоанализ урока математики позволяет управлять процессом обучения школьников и ...
... оказывают положительное воздействие на развитие памяти и мышления, воспитания воли, привычки к систематическому учебному труду и самоконтролю, повышение ответственности за выполняемую работу. Комплексное использование всех возможностей контроля и оценки успеваемости учащихся, в конечном счете, направлено на обеспечение высокого качества процесса обучения и подготовки учащихся. Теорией и ...
... , развивающая логическое и системное мышление, в свою очередь занимает достойное место в истории, помогая лучше ее понять. Как, решая проблему формирования интереса учеников к учению, использовать возможности двух школьных предметов? Сведения из истории математики, задачи исторического характера, софизмы - лишь немногие "точки соприкосновения" этих, казалось бы, далеких, но достаточно близких наук ...
0 комментариев