Навигация
Решите неравенство (решение полностью обоснуйте)
4. Решите неравенство (решение полностью обоснуйте)
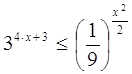
5. Докажите, что из неравенства ![]() следует неравенство
следует неравенство 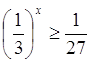 .
.
В – 2.
1. Каждому уравнению и неравенству сопоставьте решение:
(1) 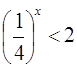
(2) 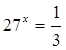
(3) 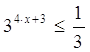
(4) ![]()
(5) ![]()
(6) ![]()
(7) ![]()
(8) ![]()
Решения: 1) 5, 2) ![]() , 3)
, 3) ![]() , 4)
, 4) ![]() , 5)
, 5) ![]() , 6)
, 6) ![]() , 7) 3, 8) -1, 9) 1,
, 7) 3, 8) -1, 9) 1,
10) ![]() , 11) уравнение решений не имеет, 12)
, 11) уравнение решений не имеет, 12) ![]() , 13)
, 13) ![]() , 14) неравенство решений не имеет, 15) 2, 16)
, 14) неравенство решений не имеет, 15) 2, 16) ![]() , 17) 0.
, 17) 0.
2. 1) Продолжите: Показательным неравенством называется неравенство…
2) Какое свойство используется при решении показательных уравнений? Сформулируйте его.
3. График функции ![]() расположен ниже графика функции
расположен ниже графика функции ![]() при
при ![]() . Объясните почему.
. Объясните почему.
4. Решите неравенство (решение полностью обоснуйте)
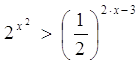
5. Докажите, что из неравенства ![]() следует неравенство
следует неравенство ![]() .
.
Приложение № 7.
Результаты итогового контроля.
| Номер задания | Оценка | ||||||
| № | Фамилия ученика | 1 | 2 | 3 | 4 | 5 | |
| 1 | Анашкина Е. | ± | + | + | + | - | «4» |
| 2 | Блинов И. | ± | + | ± | + | - | «3» |
| 3 | Гырдымов Е. | + | + | - | ± | - | «3» |
| 4 | Долгополов П. | отсутствовал | |||||
| 5 | Елсукова А. | + | + | + | + | ± | «4» |
| 6 | Жукова Э. | ± | + | ± | + | - | «3» |
| 7 | Ишутинов А. | ± | + | - | - | - | «2» |
| 8 | Казаков К. | + | + | + | + | - | «4» |
| 9 | Клыпина К. | + | + | + | + | - | «4» |
| 10 | Кодолов Е. | + | + | + | + | + | «5» |
| 11 | Колпаков Д. | + | + | + | + | - | «4» |
| 12 | Крестьянинов А. | + | + | + | + | + | «5» |
| 13 | Кузнецова Ю. | + | + | - | + | - | «3» |
| 14 | Михеев А. | + | + | + | + | + | «5» |
| 15 | Нетцель Р. | ± | ± | - | - | - | «2» |
| 16 | Панихина М. | + | + | + | + | + | «5» |
| 17 | Перешеин В. | + | + | + | + | + | «5» |
| 18 | Росина М. | ± | + | + | + | + | «4» |
| 19 | Салахова А. | + | + | + | + | + | «5» |
| 20 | Тугаринов С. | + | + | + | + | - | «4» |
| 21 | Царева И. | ± | + | + | + | - | «4» |
| 22 | Шатунов А. | + | + | - | ± | - | «3» |
| 23 | Шулятьев Е. | ± | + | + | + | + | «4» |
| 24 | Шустова И. | ± | + | - | + | - | «3» |
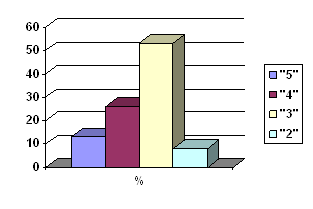
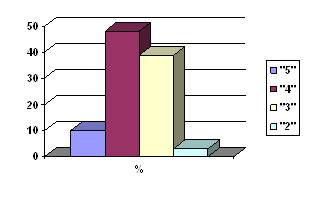
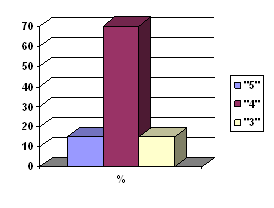
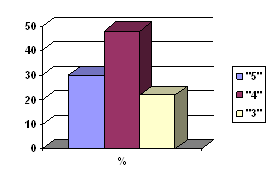
| Процент выполнивших задание | 65% | 96% | 65% | 83% | 35% | ||
Литература.
1. Алгебра и начала анализа: Учеб. Для 10-11 кл. общеобразоват. Учреждений / М. А. Алимов, Ю. М. Колягин, Ю. В. Сидоров и др. – М.: Просвещение,2002.
2. Алгебра и начала анализа в 9-10 кл.: Пособие для учителя / Л.О. Денищева, Ю.П. Дудницын и др. – М.: Просвещение, 1988.
3. Бабанский Ю.К. Оптимизация учебно-воспитательного процесса. – М.: Просвещение,1982.
4. Большой энциклопедический словарь / гл. ред. А. М. Прохоров. – М.: Научное издательство «Большая Российская Энциклопедия», 1999.
5. Бородуля И.Т. Показательные и логарифмические уравнения и неравенства. Пособие для учителей. М., «Просвещение», 1967.
6. Брейтигам Э. К., Тевс Д. П. Интегрированные уроки математики и информатики.// Информатика и образование. 2002. №2. – с. 89-94.
7. Волович М.Б. Наука обучать./ Технология преподавания математики. – М.: LINKA – PRESS,1995.
8. Воспитание учащихся при обучении математике: Кн. для учителя /Сост. Л. Ф. Пичурин. – М.: Просвещение,1981.
9. Высокие технологии в педагогическом процессе: Тезисы докладов 111 междунар. научно-метод. конф. препод. вузов, ученых и специалистов. / Науч. ред. А.А. Червова. – Н.Новгород: ВГИПА,2002.
10. Груденов Я. И. Совершенствование методики работы учителя математики. – М.: Просвещение, 1995.
11. Групповая работа школьников в обучении математике / Сост. Протасов И.Ф. – Новгород,1989.
12. Гузеев Г.Г. К формализации дидактики: системный классификатор организационных форм обучения (уроков). // Школьные технологии.2002. №4.- с.49-57.
13. Гуманитарные смыслы современного образования: Материалы докладов научно-практического семинара.- Киров: Изд-во Вятского ГПУ,2001.
14. Дайри Н. Г. Основное усвоить на уроке: Книга для учителя. - М.: Просвещение, 1987.
15. Дидактика средней школы: Некоторые проблемы современной дидактики./ Под ред. М. Н. Скаткина. – М.: Просвешение, 1982.
16. Дьяченко В.К. Сотрудничество в обучении: О коллективном способе учеб. работы. – М.: Просвещение,1991.
17. Епишева О. Основные параметры педагогической технологии. // Математика. 2000. №8.- С. 1-4.
18. История педагогики и образования. От зарождения воспитания в первобытном обществе до конца XX в. / Под ред. А.И.Пискунова. – М.: ТЦ Сфера,2001.
19. Завельский Ю.В. Как подготовить современный урок.// Завуч. 2000. №4. – с. 94-97.
20. Зенкевич И.Г. Эстетика урока математики: Пособие для учителей. – М.: Просвещение, 1981.
21. Зильберберг Н.И. Урок математики: Подготовка и проведение – М.: Просвещение, 1995.
22. Зимняя И.А. Педагогическая психология. Учебник для вузов. Изд. второе, доп., испр. и перераб. – М.: Издательская корпорация «Логос»,1999.
23. Зотов Ю. Б. Организация современного урока. – М.: Просвещение, 1984.
24. Канин Е. С. Некоторые вопросы психологии обучения решению математических задач.// Математический вестник педвузов Волго-Вятского региона, выпуск 4. – Киров. 2002, с. 162-188.
25. Кан-Калик В.А. Учителю о педагогическом общении: Кн. для учителя. – М.: Просвещение, 1987.
26. Карелина Т. М. Методы проблемного обучения.// Математика в школе. 2000. № 5. – с. 31-32.
27. Карелина Т. М. О проблемных ситуациях на уроках геометрии.// Математика в школе. 1999. № 6. – с. 19-20.
28. Ксензова Г. Ю. Перспективные школьные технологии: учебно-методическое пособие.- М.: Пед. об-во России, 2000.
29. Ксензова Г. Ю. Учебное занятие: особенности и этапы // Директор школы. 2001. №4. – с. 29-31.
30. Кириллова Г. Д. Теория и практика урока в условиях развивающего обучения. – М.: Просвещение, 1980.
31. Коваленко В. Г. Дидактические игры на уроках математики. – М.: Просвещение, 1990.
32. Конаржевский Ю. А. Анализ урока. – М.: Центр «Педагогический поиск», 2000.
33. Кульневич С.В. Лакоценина Т.П. Совсем необычный урок. – Ростов н/Дону, «Учитель»,2001.
34. Культура современного урока. / Под ред. Н.Е. Щурковой. – М.: Педагогическое общество России, 2000.
35. Лукин Р. Д. Устные упражнения по алгебре и началам анализа: Кн. Для учителя / Р. Д. Лукин, Т. К. Лукина, М. С. Якунина. – М.: Просвещение, 1989.
36. Манвелов С. Г. Современный урок математики: основы методики проведения.// Математика. 1998. №36. – С.1-4.
37. Манвелов С. Г. Конструирование современного урока математики. – М.: Просвещение, 2002.
38. Мастер-класс: подготовка учителя к успешной педагогической деятельности: методическое пособие / Под ред. Г. А. Русских. – Киров: ИУУ, 2000.
39. Махмутов М. И. Современный урок. – М.:Педагогика, 1985.
40. МашароваТ.В. Педагогическая технология: личностно-ориентированное обучение. – М.: Педагогика-ПРЕСС, 1999.
41. Машарова Т. В. Педагогические теории, системы и технологии обучения. - Киров: Изд–во ВГПУ, 1997.
42. Машарова Т. В. Использование личностно-ориентированных технологий в образовании. Материалы семинара. – Киров, 2000.
43. Методика преподавания математики в средней школе: Общая методика./ А. Я. Блох, Е. С. Канин, Н. Г. Килина и др.; Сост. Р. С. Черкасов, А.А Столяр. – М.: Просвещение, 1985.
44. Методика преподавания математики в средней школе: Частная методика. Учебное пособие для студентов пед. ин-тов по физ.-мат. спец. / А.Я.Блох, В.А.Гусев, Г.В.Дорофеев и др.; Сост. В.И. Мишин. – М.: Просвещение,1987.
45. Миненкова М., Широкова О. Карточки для зачета по теме «Решение уравнений и координатная плоскость»// Математика. 2000. №17. – С.3-5.
46. Муллагалиева С. Развитие творческого отношения к математике. // Математика. 1996. №47. – с.3.
47. Непрерывное образование: опыт, проблымы, перспективы. Вып 5. / Сост. Е.Ю. Нтконова.-Самара: СИПКРО,2000.
48. Новые педагогические и информационные технологии в системе образования. / Под ред. Е.С. Полат. - М.: Издательский центр «Академия»,1999.
49. Образование в XXI веке / Материалы Всероссийской научной заочной конференции. Образование и культура на пороге XXI века. Тверь: ТГТУ,2001
50. Окунев А. А. Спасибо за урок, дети! – М.: Просвещение, 1988.
51. Онищук В. А. Урок в современной школе. – М.: Просвещение, 1981.
52. Основы технологии развивающего обучения математики: Учебное пособие. Н.Новгород: НГПУ,1997.
53. Педагогика: Учебное пособие для студентов высших педагогических учебных заведений / В. А. Сластенин, И. Ф. Исаев, Е. Н. Шиянов. – М.: Издательский центр «Академия», 2002.
54. Педагогика: учебник для студентов педагогических вузов и педагогических колледжей. / Под ред. П. И. Пидкасистого. – М.: Педагогическое общество России,2002.
55. Педагогика сотрудничества / Сост. Котряхов Н.В. – Киров, 1989.
56. Пидкасистый П. И., Портнов М. Л. Искусство преподавания. Первая книга учителя. – М.: Издательство «Российское педагогическое агентство», 1998.
57. Подласый И. П. Педагогика: Новый курс: учебник для вузов. В 2 кн. Кн. 1. Общие основы. Процесс обучения. – М.: ВЛАДОС, 2001.
58. Портнов М.Л. Уроки начинающего учителя. – М.: Просвещение, 1993.
59. Применение новых информационно-коммуникационных технологий в преподавании: Материалы междунар. конференции. – СПб.: Изд-во РГПУ им. А.И. Герцена,2001.
60. Проблемное обучение в школьном курсе математики. – Киров: ИУУ.1997.
61. Развивающее обучение: Сб. науч.-метод. статей /Под ред. В.З.Юсупова. – Киров: ВГПУ,1997.
62. Развивающие педагогические технологии: проблемы, поиски, решения. Сборник научно-методических материалов. Киров: Издательский центр ИУУ,1999.
63. Российская педагогическая энциклопедия: В 2тт./ гл. ред. В. В. Давыдов. – М.: Научное издательство «Большая российская энциклопедия», 1999.
64. Русских Г. А. Дидактические основы современного урока: Учебно-практ. пособие.- М.: Ладога-100, 2001.
65. Рыжик В. И. 25000 уроков математики. – М.: Просвещение, 1993.
66. Саранцев Г. И. Общая методика преподавания математики Саранск: Типография «Красный октябрь», 1999.
67. Селевко Г.К. Современные образовательные технологии: Учебное пособие. - М.: Народное образование,1998.
68. Ситаров В.А. Дидактика: Учеб. пособие для студ. высш. пед. учеб. заведений /Под ред. В.А.Сластенина. – М.: Издательский центр «Академия»,2002.
69. Скаткин М.Н. Совершенствование процесса обучения. – М.: Педагогика,1971.
70. Словарь – справочник по педагогике. / научный редактор: Н. М. Капустина.- Киров: Вятский государственный педагогический университет, 2000.
71. Словарь по социальной педагогике: Учеб. Пособие для студентов высш. учеб. заведений / Авт.- сост. Л.В. Мардахаев. – М.: Издательский центр «Академия»,2002.
72. Современные проблемы методики преподавания математики. / Сост. И.С. Антонов, В.А.Гусев. – М.: Просвещение,1985.
73. Сорокин Н. А. Дидактика. Учебное пособие для студентов пед. институтов. – М.: Просвещение, 1974.
74. Третьяков П.И., Сенновский И.Б. Технология модульного обучения в школе: Практико-ориенторованная монография / Под ред. П.И. Третьякова.-М.: Новая школа, 1997.
75. Уваров А.Ю. Кооперация в обучении: групповая работа: Учебно-методическое пособие. – М.: МИРОС, 2001.
76. Фридман Л. М. Психолого-педагогические основы обучения математики в школе: Учителю математики о пед. психологии. – М.: Просвещение, 1983.
77. Ходырева Е.А. Проблемы личностно ориентированного урока: Методическое пособие. – Киров: Издание Кировского областного ИУУ,2002.
78. Чередов И.М. Формы учебной работы в средней школе. – М.: Просвещение,1988.
79. Чупаха И. В, Пужаев Е. З., Соколова И. Ю. Здоровьесберегающие технологии в образовательно-воспитательном процессе. Научно - практический сборник инновационного опыта. – М.: Илекса, 2001.
80. Шамова Т. И., Давыденко Т. М. Управление образовательным процессом в адаптивной школе. – М.: Центр «Педагогический поиск», 2001.
81. Шиянов Е.Н. , Котова И.Б. Развитие личности в обучении: Учеб. пособие для пед. вузов. – М.: Академия,1999.
82. Щуркова Н.Е. Когда урок воспитывает. – М.: Педагогика, 1981.
83. Яковлев Н. М., Сохор А. М. Методика и техника урока в школе М.: Просвещение, 1985.
Похожие работы
... уроки сказки, веселые задачи в стихах, математические загадки, сказочные задачи, математические сказки, задачи занимательного характера, головоломки, кроссворды и логические задачи способствуют активизации мыслительной деятельности учащихся на уроках математики, подтвердилась. Для себя лично я усвоила правило: "Не бери игру на урок, для того чтобы развлечься. Все на уроке должно быть логически ...
... одна из ее сторон – урок. В работе доказано, что самоанализ урока является основой эффективного управления процессом обучения. Дальнейшей же перспективой исследования является рассмотрение самоанализа всей деятельности учителя как основы управления процессом обучения математике. Изложенное выше позволяет считать, что самоанализ урока математики позволяет управлять процессом обучения школьников и ...
... оказывают положительное воздействие на развитие памяти и мышления, воспитания воли, привычки к систематическому учебному труду и самоконтролю, повышение ответственности за выполняемую работу. Комплексное использование всех возможностей контроля и оценки успеваемости учащихся, в конечном счете, направлено на обеспечение высокого качества процесса обучения и подготовки учащихся. Теорией и ...
... , развивающая логическое и системное мышление, в свою очередь занимает достойное место в истории, помогая лучше ее понять. Как, решая проблему формирования интереса учеников к учению, использовать возможности двух школьных предметов? Сведения из истории математики, задачи исторического характера, софизмы - лишь немногие "точки соприкосновения" этих, казалось бы, далеких, но достаточно близких наук ...

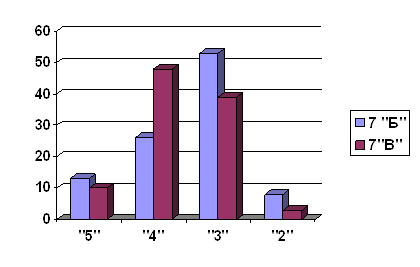
0 комментариев