Опытно-экспериментальная работа по формированию познавательной потребности у учащихся средствами информационных технологий

2. Опытно-экспериментальная работа по формированию познавательной потребности у учащихся средствами информационных технологий

2.1 Особенности изучения темы "Интеграл" в школьном курсе математики

Выбор темы "Интеграл" неслучаен. Тема "Интеграл" изучается в рамках программы 11 класса общеобразовательной школы.

Существует большое количество программ по математике, каждая из которых имеет свои особенности в изложении того или иного вопроса. В связи с этим каждая школа работает по определенной программе, в соответствии с которой разрабатывается учебный комплект, в который входят учебные пособия, книга для учителя и дидактические материалы.

В таблице 3 представлены программы по изложению темы "Интеграл" основных авторов, по которым ведется обучение математике сегодня в школах: Ш.А.Алимова, А.Н.Колмогорова, А.Г.Мордкович, С.М.Никольского.

Таблица 3 Тематическое планирование темы "Интеграл" по программам разных авторов

Автор программ	Изложение темы	Кол-во часов
А.Н.Колмогоров 11 класс	Площадь криволинейной трапеции Формула Ньютона-Лейбница Применение интеграла Контрольная работа Зачет	2 4 2 1 2
Ш.А.Алимов 11 класс	Первообразная. Правила нахождения Формула Ньютона–Лейбница Площадь криволинейной трапеции и интеграл Вычисление интеграла. Применение интеграла к решению практических задач Урок обобщения и систематизации знаний Контрольная работа	2 2 1 1 1 1
А.Г.Мордкович 11 класс	Первообразная и неопределенный интеграл Определенный интеграл Зачет Контрольная работа Учебно-тренировочные занятия по теме "Первообразная и интеграл" к ЕГЭ	3 3 2 1 5
С.М.Никольский 11 класс	Площадь криволинейной трапеции Определенный интеграл. Формула Ньютона-Лейбница Применение определенных интегралов в геометрических и физических задачах Контрольная работа	1 1 2 1 1

На основе этих программ этими авторами написаны действующие учебники. В учебниках, традиционно применяемых в школьном обучении, как правило, используются следующие подходы к введению понятия определенного интеграла.

1.   Интеграл как предел интегральных сумм.

Этот подход предполагает введение операции интегрирования как независимой операции; при этом интеграл определяется как предел последовательности, составленной из интегральных сумм. Начинается изучение в этом случае с рассмотрения конкретных задач, например, задачи о площади под кривой; задачи о работе силы и др. Затем, обобщив полученные результаты, переходят к определению интеграла как предела интегральных сумм.

Хотя данное определение громоздко, но идея метода наглядна (геометрическая интерпретация – площадь криволинейной трапеции). Вместе с определением интеграла получают и способ его вычисления. Но на практике для вычисления интеграла используют формулу Ньютона – Лейбница, которую при данном подходе необходимо доказать.

2.   Интеграл как приращение первообразной.

Этот подход предполагает введение операции интегрирования как операции, обратной дифференцированию. При этом формула Ньютона – Лейбница практически служит определением интеграла.

При этом подходе не требуется специально выводить формулу Ньютона – Лейбница, с помощью которой доказываются многие свойства интеграла. Однако в этом случае идея метода суммирования отходит на второй план. Недостаток этого подхода состоит в том, что появляются затруднения при изучении приложений интеграла. В итоге все – таки приходится рассматривать интеграл как предел интегральных сумм, чтобы получить единый, достаточно общий метод решения задач геометрии, механики, электродинамики и других разделов физики. Это рассмотрение можно провести либо сразу после введения понятия интеграла, объяснив учащимся, что не всегда возможно найти первообразную данной функции, либо непосредственно при изучении приложений интеграла, рассмотрев этот метод на одной из задач.

М. И. Башмаков дает следующее определение интеграла: "Пусть дана положительная функция f, определенная на конечном отрезке [a; b] [7]. Интегралом от функции f на отрезке [a; b] называется площадь её подграфика".

В учебнике Мордковича А. Г. "Алгебра и начала анализа" при введении понятия "Определенный интеграл" рассматриваются задачи, приводящие к данному понятию, а именно задача о вычислении площади криволинейной трапеции, задача о вычислении массы стержня и задача о перемещении точки [45]. Все три задачи при их решении приводятся к одной и той же математической модели. При чем говорится о том, что многие задачи из различных областей науки и техники приводят в процессе решения к такой же модели. Далее дается математическое описание этой модели, которая была построена в трех рассмотренных задачах для непрерывной на отрезке [a; b] функции y=f(x):

1)  разбивают отрезок [a; b] на n равных частей;

2)  составляют сумму

S_n=f(x₀)Δx₀+f(x₁) Δx₁+…+f(x_k) Δx_k+…+f(x_n-1) Δx_n-1;

3) вычисляют .

Автор учебника поясняет, что в курсе математического анализа доказано, что этот предел существует. Его называют определенным интегралом от функции y=f(x) по отрезку [a; b].

В учебнике А. Н. Колмогорова "Алгебра и начала анализа" при введении интеграла рассматривается задача о вычислении площади криволинейной трапеции [33]. Автор приводит в учебнике два способа вычисления площади криволинейной трапеции: с помощью теоремы о площади криволинейной трапеции и с помощью интегральных сумм. Второй способ сводится к определению интеграла. С помощью интегральных сумм выводятся также формулы для вычисления объемов тел, работы переменной силы, а также нахождения массы стержня и центра масс.

Среди применений интеграла в данном учебнике выводится формула для нахождения работы переменной силы, формула вычисления массы стержня и центра масс. Все формулы выводятся одним способом: с помощью интегральных сумм. Для самостоятельного решения учащимся предлагается задача о нахождении кинетической энергии стержня и несколько задач на уже рассмотренные формулы. Причем задачи делятся на несколько уровней сложности, в том числе задачи повышенной трудности.

Проведём анализ некоторых школьных учебников алгебры и начал анализа. Как мы видим из таблицы, не у всех анализируемых авторов программы совпадают. Например, в учебнике А.Н.Колмогорова "Алгебра и начала анализа" при введении интеграла рассматривается задача о вычислении площади криволинейной трапеции. Автор приводит в учебнике два способа вычисления площади криволинейной трапеции: с помощью теоремы о площади криволинейной трапеции и с помощью интегральных сумм. Второй способ сводится к определению интеграла. С помощью интегральных сумм выводятся также формулы для вычисления объемов тел, работы переменной силы, а также нахождения массы стержня и центра масс.

Среди применений интеграла в данном учебнике выводится формула для нахождения работы переменной силы, формула вычисления массы стержня и центра масс. Все формулы выводятся одним способом: с помощью интегральных сумм. Для самостоятельного решения учащимся предлагается задача о нахождении кинетической энергии стержня и несколько задач на уже рассмотренные формулы. Причем задачи делятся на несколько уровней сложности, в том числе задачи повышенной трудности.

Наиболее углублено тема "Интеграл" рассмотрена в учебнике А.Г.Мордковича [45]. В учебнике А.Г.Мордковича "Алгебра и начала анализа" при введении понятия "Определенный интеграл" рассматриваются задачи, приводящие к данному понятию, а именно задача о вычислении площади криволинейной трапеции, задача о вычислении массы стержня и задача о перемещении точки. Все три задачи при их решении приводятся к одной и той же математической модели. Причем говорится о том, что многие задачи из различных областей науки и техники приводят в процессе решения к такой же модели. Далее дается математическое описание этой модели, которая была построена в трех рассмотренных задачах для непрерывной на отрезке [a; b] функции y=f(x):

3)  разбивают отрезок [a; b] на n равных частей;

4)  составляют сумму

S_n=f(x₀)Δx₀+f(x₁) Δx₁+…+f(x_k) Δx_k+…+f(x_n-1) Δx_n-1;

3) вычисляют .

Автор учебника поясняет, что в курсе математического анализа доказано, что этот предел существует. Его называют определенным интегралом от функции y=f(x) по отрезку [a; b].

После чего автор учебника возвращается к трем рассмотренным ранее задачам и результат, полученный при их решении, переписывает следующим образом:

·           ,

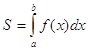где S – площадь криволинейной трапеции, ограниченной графиком функции y=f(x);

·           ,

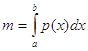где m – масса неоднородного стержня с плотностью p(х);

·           ,

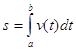где s – перемещение точки, движущейся по прямой со скоростью v=v(t).

В учебнике в физических приложениях интеграла приводятся те же задачи, что и при введении понятия интеграла, а именно задачи о массе стержня и перемещении точки. Этим автор учебника и ограничивает изучение приложений интеграла в физике.

В учебнике С.М.Никольского "Алгебра и начала анализа" рассмотрение задачи о вычислении площади криволинейной трапеции приводит к понятию интегральных сумм и пределу от них, после чего вводится определение определенного интеграла [47]. Теоретическое обоснование применения определенного интеграла рассматривается в таких физических задачах, как задачи на работу силы, работу электрического заряда, на вычисление массы стержня переменной плотности, давления жидкости на стенку и центра тяжести. Среди приложений интеграла в физике рассматриваются следующие задачи (вместе с теоретическим их обоснованием): задачи о работе силы, работе электрического заряда, задача о массе стержня переменной плотности, задача о давлении жидкости на стенку, задача о нахождении центра тяжести системы материальных точек. Однако, автор учебника приводит очень скупую систему упражнений, при чем не использует в практических задачах и половины тех формул, которые были ранее выведены.

В учебнике Ш.А.Алимова "Алгебра и начала анализа" перед введением понятия интеграла рассматривается задача о нахождении площади криволинейной трапеции, где вычисление площади сводится к отысканию первообразной F(х) функции f(x) [2]. Разность F(b)- F(a) называют интегралом от функции f(x) на отрезке [a; b]. Далее автор рассматривает вычисление площади криволинейной трапеции с помощью интегральных сумм, говорит о том, что такой способ приближенного вычисления интеграла требует громоздких вычислений и им пользуются в тех случаях, когда не удается найти первообразную функции. В качестве примеров применения интеграла приведены задачи о вытекании воды из бака и нахождении работы силы. Задачи для самостоятельного решения однотипны и их очень мало.

К учебнику А.Н.Колмогорова предполагается дидактический материал, авторами которого являются Б.М.Ивлев, С.М.Саакян, С.М.Шварцбурд [17,33]. В данном пособии содержатся самостоятельные и контрольные работы, проверочные работы, материал для итогового повторения и программированного контроля и карточки-задания для зачетов. Все они даны в соответствии с действующим учебником "Алгебра и начала анализа" под редакцией А.Н. Колмогорова.

2.2 Экспериментальная работа по формированию познавательной потребности учащихся средствами информационных технологий на примере изучения темы "Интегралы"

Экспериментальная работа проводилась в 11 "Б" классе МОУ СОШ №3 г. Абдулино Оренбургской области совместно с учителем по математике высшей категории Н.В. Николаевой. Выборку составили 20 учеников.

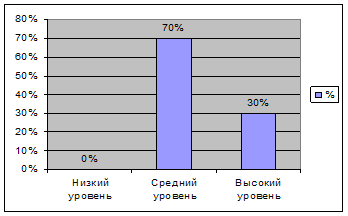
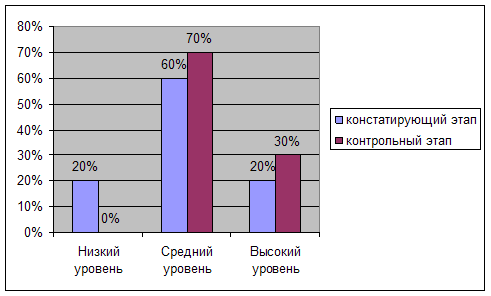
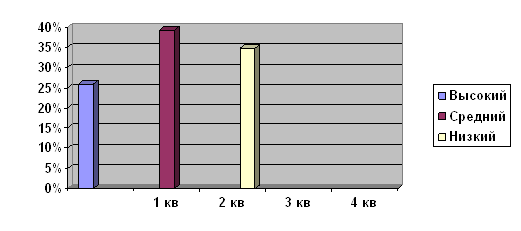
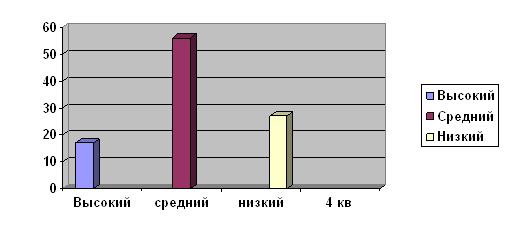
Для проверки выдвинутой нами гипотезы мы продумали и организовали педагогический эксперимент, который осуществлялся в три этапа: констатирующий, формирующий, контрольный. На констатирующем этапе нами была подобрана система методик, и по ним было проведено исследование по выявлению степени сформированности познавательной потребности у школьников. На основе анализа результатов констатирующего среза были выделены группы учащихся по уровню сформированности познавательной потребности, которые мы учитывали при организации уроков с использованием информационных технологий.

В школе, где я проходила практику, ведется преподавание по программе А.Н. Колмогорова. Исследуемая тема отражена в третьей главе учебника А.Н.Колмогорова и состоит из двух параграфов (§7 "Первообразная" и §8 "Интеграл"), что составляет 11 уроков.

При изучении темы "Интеграл" в 11 классе использовались следующие информационные технологии: интерактивная доска, мультимедийная презентация, проектор (таблица 4).

Таблица 4

№	Название темы урока	Количество часов	Применяемые ИТ
1	Интеграл. Площадь криволинейной трапеции. Вводный урок	2	Мультимедийный проектор (Power Point)
2	Формула Ньютона-Лейбница	4	Мультимедийный проектор (Power Point)
3	Вычисление интегралов и площадей криволинейных трапеций с помощью интегралов. Вычисление определенного интеграла с помощью программ MS Excel.	1	Мультимедийный проектор (Power Point), Интерактивная доска
5	Применение интегралов к решению физических задач.	1	Мультимедийный проектор (Power Point)
6	Обобщающий урок	1	Интерактивная доска, Мультимедийный проектор (Power Point)
7	Контрольная работа. Зачет	2

На уроках использовались различные формы учебной работы: фронтальная, дифференцированно-групповая, индивидуальная и индивидуализированная (самостоятельная работа, домашние задания, тесты, зачеты). Чаще всего в своей работе я проводила комбинированные уроки, которые строятся на совокупности логических не обусловленных звеньев процесса обучения. Использование познавательной потребности способствует повышению успеваемости (в особенности за счет уменьшения неудовлетворительных оценок и увеличения количества хороших оценок). Сильным ученикам особенно нравятся задания, которые требуют большего напряжения и дают дополнительную информацию, слабые же получают удовлетворение от успеха, поскольку им приходится работать со значительно более доступным материалом, чем прежде. Повышается интерес к предмету.

Рассмотрим несколько уроков.

Для начала нами был проведен вводный урок с применением электронной презентации, в котором были даны основные понятия темы (см. приложение 1). Приведем фрагмент урока по теме 1.

Урок 1.

Тема: Интеграл. Площадь криволинейной трапеции. Вводный урок

Цель: сформировать представления о криволинейной трапеции и интеграле, сформировать умения самостоятельно в комплексе применять знания, умения и навыки, осуществлять их перенос в новые условия.

Задачи:

Обучающая: создать условия для формирования представления о площади криволинейной трапеции и интеграле.

Развивающая: развивать познавательную потребность учащихся.

Воспитательная: воспитывать умение организовать свою деятельность, формирование ценностной ориентации, мировоззрения.

Оборудование: компьютер, мультимедиа проектор, экран.

Содержание урока: данный урок носит ознакомительный характер, ученики знакомятся с понятиями "площадь криволинейной трапеции", "первообразная", "интеграл", получают понятие об интеграле как площади криволинейной трапеции. Тема рассчитана на 2 часа.

План урока:

1.         Организация начала урока.

2.         Постановка проблемы урока.

3.         Актуализация ЗУН, необходимых для творческого применения знаний.

4.         Формирование новых понятий и способов действий

5.         Обобщение и систематизация знаний и способов деятельности

6.         Усвоение образца комплексного применения ЗУН

7.         Применение знаний умений и навыков в новых условиях

8.         Подведение итогов урока

Ход урока:

1. Организация начала урока. Проверка присутствующих,

2. Постановка проблемы урока. Постановка целей и задач урока.

3. Актуализация ЗУН, необходимых для творческого применения знаний.

Проиллюстрируем фрагмент урока. Чтобы заитересовать учащихся даются исторические сведения об интеграле (Слайд 2).

Формирование новых понятий и способов действий.

Определение криволинейной трапеции. Площадь криволинейной трапеции. Если на [а;b] ([а;b] ?Ох) функция у=f(х) – непрерывная, не меняет знак (график не пересекает ось абсцисс), тогда фигура, ограниченная графиком функции f, отрезком [а;b] и прямыми х = а, х = b, называется криволинейной трапецией (слайд 8).

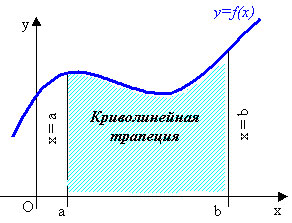
Если f - непрерывная и неотрицательная на отрезке [а;b] функция, а F – её первообразная на этом отрезке, то площадь S соответствующей криволинейной трапеции равна приращению первообразной на отрезке [а;b], т.е.

Введение понятия "интеграл".

Рассмотрим другой подход к задаче вычисления площади криволинейной трапеции. Для простоты будем считать функцию f неотрицательной и непрерывной на отрезке [а; b] тогда площадь S соответствующей криволинейной трапеции можно приближенно подсчитать следующим образом.

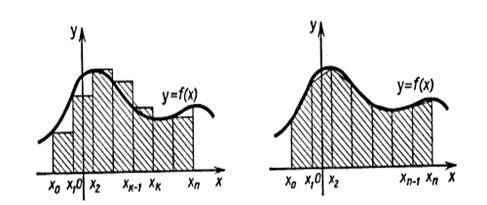
Разобьем отрезок [а; b] на n отрезков одинаковой длины точками x₀ = а<x₁ < x₂ < … <x_n-1 < x_n = b и пусть

,

где k = 1, 2, ..., n — 1, n. На каждом из отрезков [x_k-1; x_k] как на основании построим прямоугольник высотой F(x_k-1). Площадь этого прямоугольника равна:

а сумма площадей всех таких прямоугольников равна:

В силу непрерывности функции f объединение построенных прямоугольников при большом n, т. е. при малом Δx, "почти совпадает" с интересующей нас криволинейной трапецией. Поэтому возникает предположение, что Sn≈S при больших n. (Коротко говорят: "S_n стремится к S при n, стремящемся к бесконечности"— и пишут: S_n→S при n→∞.) Предположение это правильно. Более того, для любой непрерывной на отрезке [а; b] функции а (не обязательно неотрицательной) S_n при n→∞ стремится к некоторому числу. Это число называют (по определению) интегралом функции f от а до b и обозначают , т. е.

при n→∞

(читается: "Интеграл от а до b эф от икс дэ икс"). Числа а и b называются пределами интегрирования: а — нижним пределом, b — верхним. Знак называют знаком интеграла. Функция f называется подынтегральной функцией, а переменная х — переменной интегрирования. Итак, если f(х)≥0 на отрезке [а; b] то площадь S соответствующей криволинейной трапеции выражается формулой

Полный конспект урока см. приложение 1.

В теме "Применение интегралов" мы изучили площадей криволинейных трапеций с помощью интегралов. В процессе проведения опытно-экспериментальной работы нами был разработан план урока для 11 класса на тему: "Вычисление интегралов и площадей криволинейных трапеций с помощью интегралов. Вычисление определенного интеграла с помощью MS Excel" с применением интерактивных досок и информационных технологий (урок 7). Приведем фрагмент урока по теме 7 (см. приложение 1).

Тема урока: Вычисление интегралов и площадей криволинейных трапеций с помощью интегралов. Вычисление определенного интеграла с помощью программ MS Excel.

Цель: Обеспечить закрепление понятия интеграл, способы его вычисления, применение интеграла для вычисления площадей.

Задачи:

Обучающая: сформировать навыки планирования ответа, умение считать и писать в быстром темпе, навыки самоконтроля

Развивающая: развивать познавательную потребность учащихся.

Воспитательная: воспитывать умение организовать свою деятельность, формирование ценностной ориентации, мировоззрения.

Содержание урока: Данная тема рассчитана на два часа и состоит из двух частей: часть 1 – "Вычисление интегралов и площадей криволинейных трапеций с помощью интегралов. В процессе изучения данной темы учащиеся узнают о физическом приложении интеграла.

План урока:

1.         Организация начала урока.

2.         Постановка проблемы урока.

3.         Актуализация ЗУН, необходимых для творческого применения знаний

4.         Контроль и самоконтроль знаний, умений и навыков по теме интеграл

5.         Формирование новых понятий и способов действий

6.         Обобщение и систематизация знаний и способов деятельности

7.         Усвоение образца комплексного применения ЗУН

8.         Применение знаний умений и навыков в новых условиях

9.         Подведение итогов урока

Задание 2. Вычисление определенного интеграла с помощью таблицы Excel.

Для численного вычисления определенного интеграла методом трапеций используется формула:

Методику вычисления определенного интеграла в Excel с использованием приведенной формулы рассмотрим на примере.

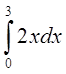
Пусть требуется вычислить определенный интеграл

Величина интеграла, вычисленная аналитически равна 9. Для численного вычисления величины интеграла с использованием приведенной формулы выполните следующие действия:

-    табулируйте подинтегральную функцию в диапазоне изменения значений аргумента 0 – 3 (см. рис.).

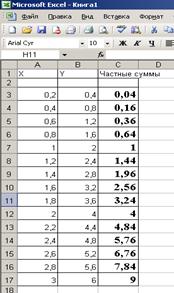
-    в ячейку С3 введите формулу =(A3-A2)*B2+(A3-A2)*(B3-B2)/2+C2, которая реализует подинтегральную функцию.

-    Скопируйте буксировкой формулу, записанную в ячейке С3 до значения аргумента х = 3. Вычисленное значение в ячейке С17 и будет величиной заданного интеграла - 9.

Вычислите интегралы, работая парами.

Это можно проиллюстрировать использованием компьютера при изучении темы "Применение определенного интеграла к вычислению площадей" на уроках математики. Подходящим программным средством в качестве компьютерной поддержки темы может использоваться электронные таблицы EXCEL. Разработка в ней задачи интегрирования позволяет, во-первых, освоить многие операции, изучаемые в программном средстве по предмету информационных технологий, и, во-вторых, закрепить материал по интегрированию в приложении к вычислению площадей. Тем самым значительно сокращаются затраты учебного времени по общим предметам. Программная разработка в EXCEL состоит из набора изучаемых функций; степенных, показательных, тригонометрических, для которых предлагается ввести соответствующие числовые коэффициенты и пределы интегрирования. В соседний столбец для каждой функции выведены формулы для вычисления первообразных с указанными коэффициентами и пределами интегрирования. После выбора функций значения интегралов и соответствующих им площадей рассматриваются автоматически. На графики выводятся подынтегральная функция и первообразная. Таким образом, имеется возможность графически и численно проанализировать характер функций и влияние на значение площади, то есть выполнить компьютерное моделирование. Поскольку первообразные находятся учащимися "ручным" способом и в электронную таблицу вводятся предварительно выведенные формулы, то работа с компьютером не сводится к механическим операциям и предполагает углубленное знакомство со свойствами функций и приобретения навыков их интегрирования. При этом представляется возможным дифференцировать темпы работы, обеспечить ее вариативность.

Так, например, нами применялись устные коллективные разминки, занимающие не более 5 минут, развивающие быстроту реакции, внимательность, умение четко и конкретно мыслить. В такие разминки следует включать вопросы, требующие однозначного, быстрого хорового ответа и направленные на актуализацию опорных знаний, и на проверку домашнего задания, и на отработку каких либо математических понятий и определений.

Для этого нами был проведен интегрированный урок.

Мотивируя применение интегрированных уроков необходимо отметить, что разнообразие занимательных форм (игры-путешествия, состязания, конкурсы, шарады, загадки) на уроках создаёт положительный эмоциональный фон деятельности, располагает к выполнению тех заданий, которые учащиеся считают трудными и непреодолимыми.

Творческие задания представляют собой один из путей, с помощью которого происходит у детей формирование познавательного интереса.

Познавательная деятельность учащихся в обучении, какой бы характер она не носила, какой бы активной она ни была, всегда должна направляться и организовываться учителем.

Тема: "Применение интеграла при решении физических задач" (см. приложение 1)

Цель: продолжить формирование умений самостоятельно в комплексе применять знания, умения и навыки, осуществлять их перенос в новые условия.

Задачи урока:

Обучающие: способствовать формированию знаний, умений по данной теме;

Развивающие: умственная деятельность (выполнять операции анализа, синтеза, делать выводы, выделять существенные признаки объектов);

Воспитательные: воспитывать умение организовать свою деятельность, формирование ценностной ориентации, мировоззрения.

Оборудование: компьютер, мультимедиа проектор, экран.

Содержание урока: данного урока нет в тематическом планировании, но нами предлагается использовать данную разработку изучении темы 7. Учащиеся знакомятся с примерами применения интеграла в физике и геометрии.

План урока:

1.         Организация начала урока.

2.         Постановка проблемы урока.

3.         Актуализация ЗУН, необходимых для творческого применения знаний

4.         Формирование новых понятий и способов действий

5.         Обобщение и систематизация знаний и способов деятельности

6.         Усвоение образца комплексного применения ЗУН

7.         Применение знаний умений и навыков в новых условиях

8.         Подведение итогов урока

Ход урока:

1.Организация начала урока.

2.Постановка проблемы урока. На прошлом уроке мы ознакомились с геометрическими задачами, которые решаются при помощи интеграла. Но интеграл применим не только в математике, другие области науки также используют его и сегодня мы с вами проверим это на примере такой науки как физика.

3.Актуализация ЗУН, необходимых для творческого применения знаний

Физические величины, вычисляемые с помощью интеграла, можно разделить на два типа, в зависимости от того, как они естественно определяются. К первому типу относятся "первичные" величины (длина пути, масса, количество электричества, количество теплоты и т. п.), т. е. такие величины, для которых другие, связанные с ними ("вторичные") величины (соответственно скорость, линейная плотность, величина тока, удельная теплоемкость и т. п.) определяются как производные этих величин. Ко второму типу относятся такие, которые определяются естественным образом как интегралы от "первичных" по отношению к ним величин (например, площадь, работа). Для первого типа величин интегральная формула для их вычисления может и должна быть доказана, опираясь на известное из предыдущего материала определение "вторичной" величины как производной от данной "первичной". Для второго типа интегральная формула появляется по определению.