Выявить средства способствующие формированию познавательной потребности у школьников, такие как информационные технологии
Именно из факта существования разных способов удовлетворения познавательной потребности вытекает факт "не насыщаемости" познавательной потребности
Среды передачи информации (почта, телевидение, радио, информационные коммуникационные сети);
Опытно-экспериментальная работа по формированию познавательной потребности у учащихся средствами информационных технологий
Формирование новых понятий и способов действий
Обобщение и систематизация знаний и способов деятельности
Вариант
Актуализация ЗУН, необходимых для творческого применения знаний
Количество электричества
Этап. Разминка – ведется на бумажном носителе
Навигация
Актуализация ЗУН, необходимых для творческого применения знаний
Формирование познавательной потребности у учащихся средствами информационных технологий
139322
знака
14
таблиц
40
изображений
3. Актуализация ЗУН, необходимых для творческого применения знаний
Физические величины, вычисляемые с помощью интеграла, можно разделить на два типа, в зависимости от того, как они естественно определяются. К первому типу относятся "первичные" величины (длина пути, масса, количество электричества, количество теплоты и т. п.), т. е. такие величины, для которых другие, связанные с ними ("вторичные") величины (соответственно скорость, линейная плотность, величина тока, удельная теплоемкость и т. п.) определяются как производные этих величин. Ко второму типу относятся такие, которые определяются естественным образом как интегралы от "первичных" по отношению к ним величин (например, площадь, работа). Для первого типа величин интегральная формула для их вычисления может и должна быть доказана, опираясь на известное из предыдущего материала определение "вторичной" величины как производной от данной "первичной". Для второго типа интегральная формула появляется по определению.
4. Формирование новых понятий и способов действий
При введении понятия интеграла как предела интегральных сумм довольно наглядным и понятным для учащихся является пример задачи о давлении жидкости на стенку.
Задача. Бассейн высоты H наполнен водой. Вычислить давление воды на прямоугольную стенку бассейна с основанием прямоугольника, равным а.
Разделим высоту Н на n равных частей (Δh). Стенка разделится на "элементы". Так как кубометр воды весит тонну, то давление столба жидкости высоты hi м, имеющего сечение 1 м2, равно hi тоннам.
Давление же воды на элемент, находящийся на глубине hi, равно произведению hi на площадь элемента: hia Δh. Обозначим произведение hia через F(hi). Тогда величина давления на всю стенку приближенно равна
Pn≈ F1(h1)Δh1+…+Fn(hn) Δhn.
Данную сумму называют интегральной суммой функции F(h) на отрезке [0; H]. При этом предполагается, что функция F(h) непрерывна на отрезке [0; H] и может принимать любые значения. Если 
и высоты "элементов" стремятся к нулю, то точное выражение суммы равно 
. Его называют определенным интегралом от функции F(h) на отрезке [0; H] и обозначают
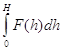
Далее понятие определенного интеграла обобщается на произвольную непрерывную функцию F(x) и произвольный отрезок [a; b].
Рассмотрим несколько задач с физическими моделями, где интеграл определяется как приращение первообразной.
1. Задача о перемещении точки.
Пусть v=v(t) скорость прямолинейного движения точки, заданная на некотором промежутке времени [t1; t2]. При этом пусть v(t)>0. Как выразится длина пути, пройденного точкой за данный промежуток времени?[5]
Обозначим координату движущейся точки в момент t через S(t). Тогда, так как движение при v>0 происходит только в положительном направлении (или иначе, т. к. S(t) – функция возрастающая, ввиду того, что 
), то искомое расстояние будет выражаться числом S(t2)-S(t1). С другой стороны S(t) есть первообразная функции v(t) (
). Таким образом вычисление длины пути, пройденного точкой за данный промежуток времени, сводится к отысканию первообразной S(t) функции v(t), т. е. к интегрированию функции v(t).
Разность S(t2)-S(t1) называют интегралом от функции v(t) на отрезке [t1; t2] и обозначают так:
.
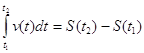4. Импульс силы.
Пусть на тело массой m в течение времени t действует какая-то сила F(t). Найти количество движения тела при заданной зависимости силы от времени за промежуток времени [t1; t2].
Как известно из физики второй закон Ньютона в импульсном представлении выражает уравнение
ΔР=FΔt
Произведение P=mv(t) массы на скорость называется "количеством движения". Так как скорость тела зависит от времени, то за промежуток времени [t1; t2] искомое количество движения может быть найдено так: Р(t2)-Р(t1). С другой стороны Р(t) есть первообразная функции F(t). Таким образом вычисление количества движения тела за данный промежуток времени, сводится к отысканию первообразной Р(t) функции F(t).
Разность P(t2)-P(t1) называют интегралом от функции F(t) на отрезке [t1; t2] и обозначают так:
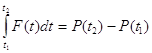
Величина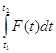 
называется также "импульсом силы" за время [t1; t2]. Словесная формулировка результата: изменение количества движения равно импульсу силы.
Похожие работы
... уровня сформированности познавательного интереса к учебной деятельности у младших школьников. 2 этап – формирующий этап - организована работа по повышению познавательного интереса учащихся к учебной деятельности с использованием современных информационных технологий. 3 этап – контрольный этап - повторная диагностика уровня сформированности познавательного интереса к учебной деятельности у ...
... Таким образом, в современном мире необходимы информационно-коммуникационные технологии. ГЛАВА II. ОПЫТНО-ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ ПО ТЕМЕ: «ИНФОРМАЦИОННО-КОММУНИКАЦИОННЫЕ ТЕХНОЛОГИИ КАК СРЕДСТВО РАЗВИТИЯ ПОЗНАВАТЕЛЬНОГО ИНТЕРЕСА ПРИ ИЗУЧЕНИИ ЖИВОТНОГО МИРА В НАЧАЛЬНОЙ ШКОЛЕ» 2.1 Диагностика уровня развития познавательного интереса В результате изучения психолого-педагогической литературы ...
... компьютера позволяет не только многократно повысить эффективность обучения, но и стимулировать учащихся к дальнейшему самостоятельному изучению английского языка, что и было доказано в ходе эксперимента. Таким образом согласно итогам нашего исследования, использование новых информационных технологий, в частности, компьютера в условиях сельской школы является эффективным: Оно создало комфортные ...
... это? Почему? Обоснованные доказательства с привлечением фактического материала Вопросы В чём его суть? Обоснованные доказательства сути неизвестного явления Формирование познавательной способности старшеклассников на уроках истории таджикского народа в школе не может осуществляться без постоянного управления со стороны педагогов. Это означает, что педагогический коллектив строго следит за ...
0 комментариев