Вариант

2 вариант

X
	Х			X
		X
		X
		X

Знак "Х" означает места прорезей в шаблоне.

Оценка результатов:

6 крестиков верных – "5";

5 крестиков верных – "4";

4 крестика верных – "3";

3 и меньше – "2".

6) Индивидуальное проблемное задание для тех, кто быстро справился с самостоятельной раньше других:

При каком положительном значении параметра а площадь фигуры, ограниченной линиями y= 1/x², y=0, x=1, x=a равна 7/8?

3. Подведение итогов урока

Подводится итог урока. Цель нашего урока была обобщить знания по теме "Первообразная. Интеграл." Давайте посмотрим как мы работали. На экран с помощью проектора выводится таблица. Поднимите руку, если вы

- знаете таблицу первообразных;

- умеете пользоваться таблицей для нахождения первообразной сложной функции;

- легко находите площадь криволинейной трапеции;

- умеете применять интеграл для решения физических задач.

Те, кто поднял руку на все вопросы, готовы к выполнению контрольной работы. Остальным надо подготовиться лучше. Выставляются оценки за работу на уроке. Задаётся домашнее задание.

Для развития познавательной потребности нами предлагается во внеклассной форме работы использование различных видов уроков для развития познавательной потребности учащихся. Мы, например, использовали урок-КВН (см. приложение 1).

Урок КВН по теме "Интеграл"

Цель: обобщение изученного материала по теме, формирование умений применять математические задания к решению практических задач.

Задачи:

Развивающие: развитие познавательной потребности, творческих способностей.

Воспитательные: воспитание интереса к предмету, воспитание чувства коллективизма и взаимовыручки.

КВН проводится интерактивно с помощью сайта школы.

На экране ЭВМ написано:

I команда

II команда

(Ниже ведётся запись полученных очков).

Правила игры.

Класс разбивается на две команды.

Выбираются капитаны команд.

Капитаны назначают консультантов.

Для участия во всех видах работы ученики вызываются к доске капитанами команд.

Ход урока.

1 этап. Разминка – ведется на бумажном носителе.

На экране ЭВМ написаны задания.

II этап. Блиц – турнир – проводится с помощью ЭВМ (желательно применение проектора).

III этап. Домашнее задание.

К доске приглашаются по 1 ученику от каждой команды.

1. С помощью интеграла вывести формулу объёма конуса.

2. С помощью интеграла вывести формулу объёма шара.

IV этап. Конкурс капитанов.

V этап. Конкурс болельщиков – задания проектируются на доску с помощью проектора, а также дублируются на сайте школы.

VI этап. Конкурс эрудитов - задания проектируются на доску с помощью проектора, а также дублируются на сайте школы

1. Вычислите:

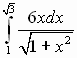
2. Вычислите:

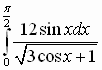
Решение 1.

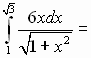
Пусть

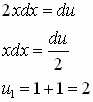
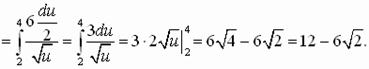
Решение 2.

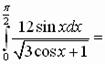
Пусть

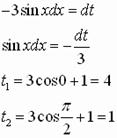
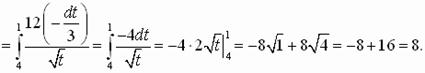
VII этап. Конкурс консультантов. (дополнительный) – проводится при помощи Mathcad.

VIII этап. Подведение итогов.

Выигравшая команда объявляется победительницей, а многие учащиеся получают оценки.

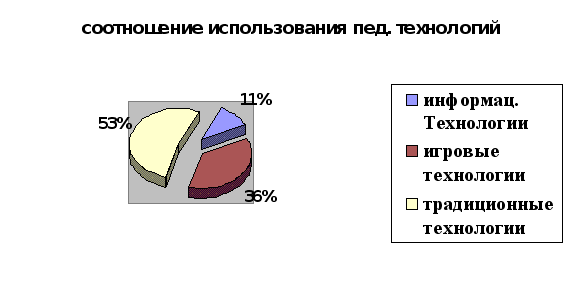
Итак, применение информационных технологий в преподавании темы "Интегралы":

1.         Содействует воспитанию аккуратности, организованности, дисциплины;

2.         Формирует умения работать коллективно, в группе, паре, самостоятельно;

3.         Прививает интерес к предмету посредством применения современных информационных технологий;

4.         Способствует развитию интеллектуальных качеств личности школьника: самостоятельность, гибкость, способности видеть проблему, обобщать, переключаться с одного вида работы на другой;

5.         Развивает эмоции учащихся, создавая эмоциональные ситуации удивления, сопереживания;

6.         Развивает познавательный интерес, создавая игровые ситуации.

2.3 Результаты экспериментальной работы

Для исследования сформированности познавательной потребности школьников нами был подобран комплекс методов: "Познавательный интерес", "Познавательная потребность", "Мое учение".

Для выявления познавательного интереса была применена методика "Познавательного интереса", целью которой является установление характера и силы познавательного интереса (см. приложение 2). Анализ результатов данной методики приведены в таблице 5.

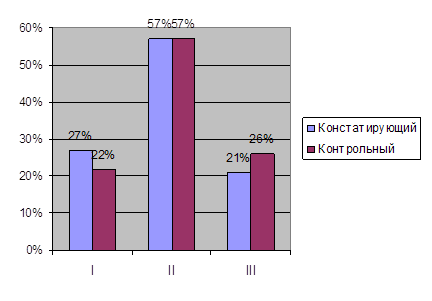
Таблица 5 Анализ результатов констатирующего и контрольного срезов изучения уровня познавательного интереса

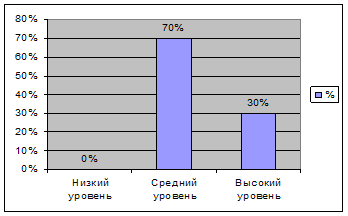
Из таблицы 4 видно, что произошла динамика в характере и силе познавательного интереса у учащихся к учебе. У учеников увеличился интерес к учебе, приблизительно 1,25 раз. Наиболее наглядно, полученные данные можно увидеть на диаграмме 1.

Диаграмма 1 Уровень познавательного интереса

Для изучения познавательной потребности была применена методика "Познавательная потребность", целью которой является установление интенсивности познавательной потребности у учащихся (см.приложение 2, анкета 2). Анализ полученных данных помещен в таблицу 6.

Таблица 6 Анализ результаты изучения познавательной потребности школьников

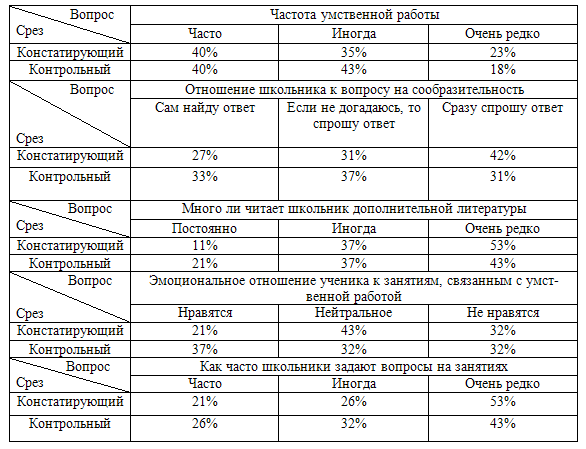
Как мы видим, из таблицы 6, произошла динамика роста познавательной потребности:

1.   Увеличилась умственная работа школьников, при задании на сообразительность учащиеся предпочитают самостоятельный поиск ответа (+6%), стали больше читать дополнительной литературы (+10);

2.   На 16% увеличилось эмоциональное отношение учащихся к интересным занятиям, связанным с умственной работой.

3.   Учащиеся стали чаще задавать вопросы, что свидетельствует о возросшем интересе к учебному материалу.

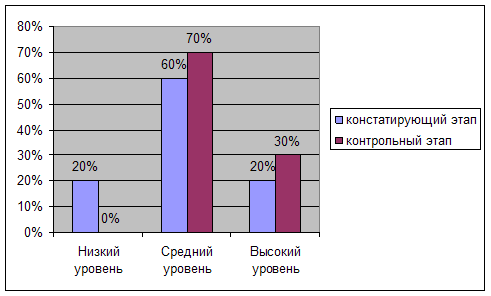
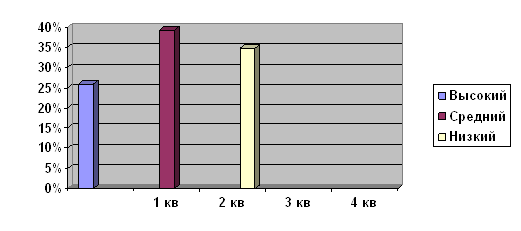
Этот факт наглядно демонстрируют диаграммы 2-3.

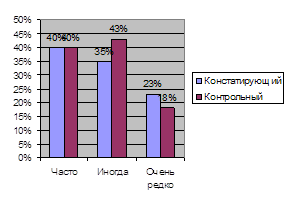
Диаграмма 2 Частота умственной работы

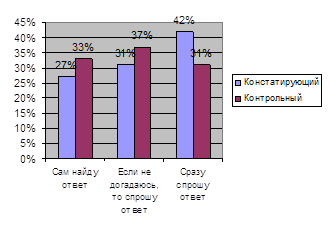
Диаграмма 3 Отношение школьника к вопросу на сообразительность

Для выявления отношения школьников к учению, предметную направленность их познавательных интересов, изучить некоторые особенности процесса самостоятельной деятельности учащихся мы воспользовались методикой "Мое учение" (см. приложение 2, анкета 3). Результаты этого исследования представлены в таблице 7.

Таблица 7 Сравнительный анализ результатов методики "Мое учение" (в %)

Этап	I			III			IV	V
	1	2	3	1	2	3
Констатирующий	92	0	8	20	68	12	76	24
Контрольный	96	0	4	12	80	8	64	36

Этап	VI			VII
	1	2	3	1	2	3	4	5	6
Констатирующий	60	4	12	0	24	60	28	12	68
Контрольный	24	76	0	8	0	20	56	24	24

Из таблицы 7 видно, что на 4 % увеличилось число учащихся, которым интересно учиться в школе; на 12 % возросло число учеников, чувствующих себя всегда спокойно при выполнении самостоятельных работ и 44 % учеников научились правильно распределять время при выполнении самостоятельных работ.

В процессе опытно-экспериментальной работы выявлены два наиболее значимых направления использования информационных технологий в образовании: как средства обучения и как инструментов познания. Первый подход таит в себе ряд проблем, связанных с усвоением уже готовой информации, при котором отсутствует творческая компонента усвоения. Другой подход – использование компьютерных средств как инструментов познания является наиболее продуктивным подходом к обучению, Инструментами познания являются различные компьютерные средства, предназначенные для организации и облегчения процесса познания. Именно с таким подходом связывается дальнейшее развитие использования информационных технологий в обучении. В этом случае учащийся под управлением преподавателя проходит путь познания самостоятельно, а не является потребителем уже готовых знаний, что способствует более глубокому и осознанному усвоению материала, развитию умений разрабатывать учебные компьютерные программы.

Экспериментальная проверка показала, что разработанная методика обучения учащихся 10-11 классов способствует повышению у учащихся уровня знаний в области интегрального исчисления; уровня познавательной потребности; готовности к использованию информационных технологий в будущем.

Использование компьютера в качестве средства обучения путем применения прикладных программ в качестве формализмов представления знаний способствует более быстрому и более полному усвоению материала, чем при использовании всех имеющихся в настоящее время обучающих компьютерных программ.

Сравнительный анализ контрольного констатирующего среза показали, что произошла динамика роста, хоть и не значительная. Таким образом, наша гипотеза подтвердилась.

Заключение

Итак, познавательная потребность – это, прежде всего потребность в новой информации, однако сама новая информация может выступать в самых различных формах: в новом стимуле (новый цвет предмета, неожиданный звук, необычная форма), в новом знании о предмете (его назначение, устройство и т.д.), и наконец, в новой системе представлений о мире (научные знания, наука в целом). И самые элементарные и самые сложные способы удовлетворения познавательной потребности в целом характеризуют одну и ту же познавательную потребность, однако в зависимости от этих способов различаются уровни развития познавательной потребности.

В классных коллективах, где познавательная потребность достигает такого уровня развития, встречаются отдельные учащиеся, у которых она перерастает в страсть, в жажду раздумий над предметом. Это обычно учащиеся с выдающимися способностями.

Современный этап применения информационной технологии обучения в учебном процессе заключается в использовании компьютера как средства обучения не эпизодически, а систематически с первого до последнего занятия при любом виде обучения. Основная проблема при этом заключается в методике компьютеризации курса, который предстоит освоить обучаемому. Возможна либо полная перестройка и ориентация на создание новых компьютеризованных курсов, либо реализация методики с частичной компьютерной поддержкой курса. Другими словами речь идет о форме компьютерной поддержки процесса обучения. В настоящее время практика использования информационных технологий в образовании обнаруживает две тенденции:

- применение промышленных универсальных информационных программ, предназначенных для решения широкого круга практических и научных задач из различных предметных областей, и адаптированных к учебным дисциплинам;

- применение обучающих программ, специально разработанных для целей обучения и реализующих соответствующие методики, заложенные в них разработчиками. На сегодняшний день существует широкий спектр программ от простейших, контролирующих до сложных мультимедийных продуктов.

Использование информационных технологий в обучении позволяет у большинства детей со склонностями к техническим наукам развить устойчивый интерес к данным предметам. При этом решается ещё одна задача образовательного процесса - его гуманизация. Каждый ребенок находит себе задание по своим силам, уровню подготовки и интереса.

Для исследования познавательной потребности нами была подобрана система методов. Данное исследование проводилось в три этапа: констатирующий формирующий и контрольный.

По результатам проведенных методик мы увидели, что произошла динамика роста познавательной потребности: приблизительно на 4,5% увеличилась умственная работа школьников, при задании на сообразительность, учащиеся предпочитают самостоятельный поиск ответа, стали больше читать дополнительной литературы, так же приблизительно на 4,5% увеличилось эмоциональное отношение к интересным занятиям, связанным с умственной работой. Учащиеся стали чаще задавать вопросы, что свидетельствует о возросшем интересе к учебному материалу, таким образом, наша гипотеза подтвердилась.

Список литературы

1.         Азевич А.И. Несколько компьютерных программ. //Математика в школе. – 2002. - №10. – С.41-43.

2.         Алимов Ш. А. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк./ Ш. А. Алимов, Ю. М. Колягин, Ю.В. Сидоров и др. - М.: Просвещение, 1993. – 254 c.

3.         Анастази А. Психологическое тестирование. Кн. 2: Пер. с англ./Под ред. Туревича К.М., Лубовского В.И. – М.: Педагогика, 1982. – 365 с.

4.         Аут К.Х., Виленкин Н.Я. О роли основных принципов дидактики в преподавании школьного курса математики. //Математика в школе. – 1987. - №1. - С.41-47.

5.         Ахметгалив А. Мотивация деятельности на уроках математики. //Математика в школе. – 1996. - №2. – С.57-62.

6.         Барчунова Ф. Развитие познавательного интереса к геометрии учащихся VI–VII классов. //Математика в школе. – 1974. - №6. – С.21-28.

7.         Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. - М.: Просвещение, 1992. – 351 с.

8.         Белова О.Е. Об использовании компьютерных технологий в процессе изучения темы "Определенный интеграл и его приложения" //Математическая и методическая подготовка студентов педвузов и университетов в условиях модернизации системы образования: Материалы XXII Всероссийского семинара преподавателей математики педвузов и университетов – Тверь: Изд-во ТГУ, 2003.

9.         Белова О.Е. Особенности методической системы обучения интегральному исчислению студентов педвузов на основе использования информационных технологий //Вестник КрасГУ (Гуманитарные науки). – Красноярск: ИЦ КрасГУ, 2006. – Вып.3. – С.81–84.

10.      Берман Г. Н. Сборник задач по курсу математического анализа: Уч. пособие. - СПб.: Изд-во "Профессия", 2001. – 432 с.

11.      Божович Л.И. Проблемы развития мотивационной сферы ребенка. В кн.: Изучение мотивации поведения детей и подростков /Под ред. Л.И. Божович, Л.В. Благонадежной – М., 1972.

12.      Бокуть Л.В. Компьютерные технологии для эффективной познавательной деятельности. //Минск: Материалы международной научно - метод. конф. "Высшее техническое образование: проблемы и пути развития", - 2004. - С.166-167.

13.      Будунов Г. М. Компьютерные технологии в образовательной среде: "за" и "против". – М.: АРКТИ, 2005. – 234с

14.      Виленкин, Н. Я., Куницкая, Е. С., Мордкович, А. Г. Математический анализ. Интегральное исчисление: Уч. пособие для студентов-заочников II курса физико-математических факультетов педагогических институтов. - М.: Просвещение, 1979. – 175 с.

15.      Виштынецкий Е.И. Применение информационных технологий в сфере образования и обучения [Электронный ресурс] Режим доступа: http://www.snfpo.ru/help/articles/a1.htm

16.      Выготский Л.С. Собрание сочинений: В 6 томах. Том 4. Детская психология /Под ред. Эльконина Д.Б. – М.: Педагогика, 1984. – 432 с.

17.      Гальперин П.Я., Котик Н.Р. К психологии творческого мышления //Вопросы психологии. – 1982. - №5. – С. 23-26.

18.      Гузеев В.В. Инновационные идеи в современном образовании //Школьные технологии. – 1997. – №1. - С.47-52.

19.      Давыдов В.В. Теория развивающего обучения. - М.: Педагогика, 1986.-240 с.

20.      Дразкин И.Е. Опыт системы преподавания математики. //Математика в школе. – 1996. - №6. – С.35-39.

21.      Дружинин В.Н. Психология общих способностей.–СПб.: Питер, 1999.–368 с.

22.      Дьюи Д. Психология и педагогика мышления. /Пер. с англ. Николаевой Н.М., под ред. Виноградова Н.Д. – М.: Совершенство, 1997. – 208 с.

23.      Задачи как средство обучения алгебре и началам анализа в X классе [Текст]: Уч. Пособие //Сост. Е. С. Канин. – Киров: Редакционно-издательский совет Кировского ГПИ имени В. И. Ленина, 1985. – 92 c.

24.      Задачник по курсу математического анализа: Уч. пособие для студентов заочн. отделений физ.-мат. фак-тов пединститутов. Ч. I //Под ред. Н. Я. Виленкина. – М.: Просвещение, 1971. – 343 с.

25.      Захарова И.Г. Информационные технологии в образовании: Учебное пособие для студ. высш. пед. учеб. заведений. - М.: Издательский центр "Академия", 2003. – 192 с.

26.      Зельдович, Я. Б. Высшая математика для начинающих и её приложения к физике: Уч. пособие для физико-математических средних школ и проведения факультативных занятий. – М.: Наука, 1970. – 560 с.

27.      Интернет в гуманитарном образовании: Учеб. Пособие для студ. вузов /Под ред. Е.С.Полат. — М.: Гуманит. Изд. Центр ВЛАДОС, 2001. — 272 с.

28.      Капустина Т.В. Компьютерная система "Mathematica 3.0" //Математика в школе. - 2003. - №7. – С. 35-37.

29.      Кастро К., Альфтан Т. Компьютеры во внешкольном образовании //Перспективы: вопросы образования. - М., 1991. - № 2. – С. 45-49.

30.      Кларин М.В, Инновационные модели обучения в зарубежных педагогических поисках. Пособие к спец. курсу для вузов, институтов усовершенствования учителей, повышения квалификации работников образования. - М.: Арена, 1994. – 128 с.

31.      Когаловский М.Р. Перспективные технологии информационных систем. – М.: Мастерство, 2001. –256 с.

32.      Кождаспирова Г.М., Коджаспиров А.Ю. Педагогический словарь. – М.: ACADEMIA, 2000.

33.      Колмогоров, А. Н. Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений/ А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др. – М.: Просвещение, 1998. – 365 c.

34.      Косов Б.Б. Творческое мышление восприятие и личность. – М.: "Институт практической психологии", Воронеж: НПО "МОДЕК", 1997 –47 с.

35.      Краткий психологический словарь /Ред.-сост. Л.А.Карпенко; /Под общ. ред. А.В.Петровского, М.Г.Ярошевского. - 2-е изд. - Ростов н/Д: Феникс, 1998. - 512 с.

36.      Кривоногов В.В. Нестандартные задания по математике: 5-11 классы. – М.:Издательство "Первое сентября", 2003. – 224с

37.      Крутецкий В.А. Психология математических способностей школьников. - М.: Просвещение, 1968 – 432с.

38.      Кузьмина В.Г. Активизация познавательной деятельности учащихся. //Математика в школе. – 1996. - №4. – С.12-16.

39.      Кухарь А.В. Некоторые пути формирования познавательного интереса у учащихся IV–V классов. //Математика в школе. – 1985. - №5. – С.20-26.

40.      Леонтьев А.Н. Избранные психологические произведения: В 2 т. – Т II. – М., 1983. – 467 с.

41.      Математика 10-11 классы: методическое пособие для учителя / И.И.Зубарева, А.Г. Мордкович. – 3-е изд., испр. – М.: Мнемозина, 2008. –104с.

42.      Математика 10-11 классы: развернутое тематическое планирование. Линия Г. В. Дорофеева / авт.-сост. Т.Н. Видеман. – Волгоград: Учитель, 2009.– 71 с.

43.      Математика. 11 класс: Поурочные планы по учебнику Н.Я. Виленкина, В.И. Жохова. II полугодие /Авт.- сост. Л.А. Тапилина, Т.Л. Афанасьева. – Волгоград.: Учитель, 2005. – 144 с.

44.      Мигунова Н.П. Некоторые приемы активизации познавательной деятельности учащихся. //Математика в школе. – 2000. - №6. – С.10-15.

45.      Мордкович А. Г. Алгебра и начала анализа [Текст]: Учеб. для 10-11 кл. общеобразоват. учреждений. Ч. I. – М.: Мнемозина, 2003. – 375 с.

46.      Никольский С. М. Алгебра и начала анализа [Текст]: Учеб. для 11 класса общеобразоват. учреждений/ С. М. Никольский, М. К. Потапов. - М.: Просвещение, 2003.

47.      Нифагин В.А., Бокуть Л.В. Обучение математическому моделированию на основе электронных пособий. //Минск: Материалы II-й международной научно-метод. конф. "Дистанционное обучение - образовательная среда XXI века", 2002. - С.122-123.

48.      Новые педагогические и информационные технологии в системе образования: Учебное пособие для студентов пед. вузов и системы повышения квалификации пед. кадров / Е.С. Полат, М.Ю. Бухаркина, М.В. Моисеева, А.Е. Петров; Под ред. Е.С. Полат. – М.: Издательский центр "Академия", 2003. – 272 с.

49.      Овечкина О.И. Приемы активизации познавательной деятельности. //Математика в школе. – 1993. - №5. – С.4-8.

50.      Программы для общеобразовательных учреждений. Математика. – МОРФ. – 63 с.

51.      Ретинская И.В., Шугрина М.В. Отечественные системы для создания компьютерных учебных курсов //Мир ПК. — 1993. — № 7.- С 12-14

52.      Роберт И.В. Современные информационные технологии в образовании: дидактические проблемы; перспективы использования. М.: Школа-Пресс. 1994.— 205 с

53.      Рубинштейн С.Л. Основы общей психологии. В 2 т. – Т 1 –М.,1989. – 720 с.

54.      Скатецкий В.Г. Организационно-методические связи преподавания математики на факультетах нематематического профиля // Высшая школа. 1999, № 2, С. 45-49.

55.      Старцева Н.А. Применение электронных пособий на уроках математики //Информационные технологии в образовании. Сб. научно - методических материалов. - Новосибирск: НГУ, 2004. – С.23 -26

56.      Тихомирова О.К. Познавательная потребность. //Сб. "Проблемы формирования социогенных потребностей". Тбилиси, 1974, с. 102—105.

57.      Хохлова Н.М. Информационные технологии. - М.: Приор-издат, 2007.–192 с.

58.      Хрестоматия по общей психологии. Психология мышления /Под ред. Ю.Б.Гиппенрейтер, В.В.Петухова. – М., МГУ, 1987. –276 с.

59.      Хуторской А.В. Интернет в школе: Практикум по дистанционному обучению. - М.:ИОСО РАО, 2000. - 304 с.

60.      Черников Б.В. Информационные технологии управления: учебник. – М.:ИД "ФОРУМ" : ИНФРА – М, 2009. – 352 с.

61.      Черняк А.А., Черняк Ж.А., Доманова Ю.А. Высшая математика на базе MATHCAD. Общий курс. - С-Пб: БХВ-Петербург, 2004. -54 с.

62.      Яковлева Е.А. Развитие творческого потенциала у школьников. //Вопросы психологии. – 1997. - №2. - С.37-42.

Приложение 1

Урок 1

Тема: Интеграл. Площадь криволинейной трапеции.

Цель: сформировать представления о криволинейной трапеции и интеграле, сформировать умения самостоятельно в комплексе применять знания, умения и навыки, осуществлять их перенос в новые условия.

Задачи урока:

Обучающая: создать условия для формирования представления о площади криволинейной трапеции и интеграле.

Развивающая: развивать познавательную потребность учащихся.

Воспитательная: воспитывать умение организовать свою деятельность, формирование ценностной ориентации, мировоззрения.

Оборудование: компьютер, мультимедиа проектор, экран.

Содержание урока: данный урок носит ознакомительный характер, ученики знакомятся с понятиями "площадь криволинейной трапеции", "первообразная", "интеграл". Тема рассчитана на 2 часа.

План урока:

1.Организация начала урока.

2.Постановка проблемы урока.

3.Актуализация ЗУН, необходимых для творческого применения знаний.

4.Формирование новых понятий и способов действий

5.Обобщение и систематизация знаний и способов деятельности

6.Усвоение образца комплексного применения ЗУН

7.Применение знаний умений и навыков в новых условиях

8.Подведение итогов урока

Ход урока:

Сообщение учащимся темы и целей урока: Тема нашего сегодняшнего урока: Интеграл. Площадь криволинейной трапеции (Слайд 1).

Исторические сведения об интеграле (Слайд 2):

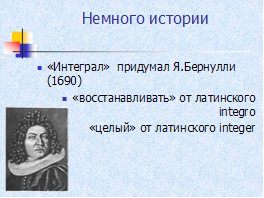
Определение криволинейной трапеции. Площадь криволинейной трапеции. Если на [а;b] ([а;b] ?Ох) функция у=f(х) – непрерывная, не меняет знак (график не пересекает ось абсцисс), тогда фигура, ограниченная графиком функции f, отрезком [а;b] и прямыми х = а, х = b, называется криволинейной трапецией (слайд 8).

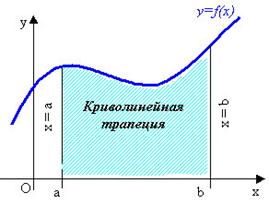
Если f - непрерывная и неотрицательная на отрезке [а;b] функция, а F – её первообразная на этом отрезке, то площадь S соответствующей криволинейной трапеции равна приращению первообразной на отрезке [а;b], т.е.

Введение понятия "интеграл".

Рассмотрим другой подход к задаче вычисления площади криволинейной трапеции. Для простоты будем считать функцию f неотрицательной и непрерывной на отрезке [а; b] тогда площадь S соответствующей криволинейной трапеции можно приближенно подсчитать следующим образом.

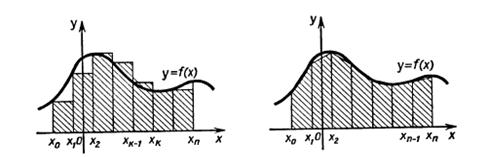
Разобьем отрезок [а; b] на n отрезков одинаковой длины точками x₀ = а<x₁ < x₂ < … <x_n-1 < x_n = b и пусть , где k = 1, 2, ..., n — 1, n. На каждом из отрезков [x_k-1; x_k] как на основании построим прямоугольник высотой F(x_k-1). Площадь этого прямоугольника равна:

а сумма площадей всех таких прямоугольников равна:

В силу непрерывности функции f объединение построенных прямоугольников при большом n, т. е. при малом Δx, "почти совпадает" с интересующей нас криволинейной трапецией. Поэтому возникает предположение, что Sn≈S при больших n. (Коротко говорят: "S_n стремится к S при n, стремящемся к бесконечности"— и пишут: S_n→S при n→∞.) Предположение это правильно. Более того, для любой непрерывной на отрезке [а; b] функции а (не обязательно неотрицательной) S_n при n→∞ стремится к некоторому числу. Это число называют (по определению) интегралом функции f от а до b и обозначают

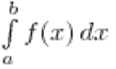, т. е.

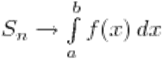при n→∞

(читается: "Интеграл от а до b эф от икс дэ икс"). Числа а и b называются пределами интегрирования: а — нижним пределом, b — верхним. Знак называют знаком интеграла. Функция f называется подынтегральной функцией, а переменная х — переменной интегрирования. Итак, если f(х)≥0 на отрезке [а; b] то площадь S соответствующей криволинейной трапеции выражается формулой

Пример: Вычислить площадь криволинейной трапеции, ограниченной линиями у = 4 - х2 и у = 0

Решение:

1. Построим криволинейную трапецию:

у = 4 - х2

- квадратичная функция, график – парабола, ветви направлены вниз.

у = 0 - ось абсцисс.

2. Найдём [а;b]:

4-х2 = 0;

х2 = 4

х = -2 или х = 2, т. е. а = -2 b = 2

3. Найдём площадь криволинейной трапеции по формуле:

S = F(b) – F(а)

Домашнее задание (Слайд 10).

Урок 2

Тема урока: Вычисление интегралов и площадей криволинейных трапеций с помощью интегралов. Вычисление определенного интеграла с помощью программ MS Excel.

Цель: Обеспечить закрепление понятия интеграл, способы его вычисления, применение интеграла для вычисления площадей.

Задачи:

Обучающая: сформировать навыки планирования ответа, умение считать и писать в быстром темпе, навыки самоконтроля

Развивающая: развивать познавательную потребность учащихся.

Воспитательная: воспитывать умение организовать свою деятельность, формирование ценностной ориентации, мировоззрения.

Содержание урока: Данная тема рассчитана на два часа и состоит из двух частей: часть 1 – "Вычисление интегралов и площадей криволинейных трапеций с помощью интегралов. Вычисление определенного интеграла с помощью программ MS Excel". Вторым часом нами был проведен интегрированный урок (физика + математика) по теме "Применение интеграла при решении физических задач"

Оборудование: интерактивная доска, рабочий листок для каждого ученика, тесты, подготовленные страницы флипчарта, лото компьютер с установленной программой MS Office 2003.

План урока:

1.         Организация начала урока.

2.         Постановка проблемы урока.

3.         Актуализация ЗУН, необходимых для творческого применения знаний.

4.         Контроль и самоконтроль знаний, умений и навыков по теме интеграл

5.         Формирование новых понятий и способов действий

6.         Обобщение и систематизация знаний и способов деятельности

7.         Усвоение образца комплексного применения ЗУН

8.         Применение знаний умений и навыков в новых условиях

9.         Подведение итогов урока

Ход урока:

Каждый из учащихся до урока получает рабочий листок ученика (см. в конце плана урока), на котором записаны этапы урока. Это может позволить учащимся работать в удобном им ритме. Именно в нём учащийся выполняет задания, и после урока лист сдаётся. Часть заданий можно проверить с помощью компьютера или интерактивной доски на уроке. Учащиеся могут выполнять задания в любой удобной для них последовательности. Выбор заданий самостоятельной работы (лото) также произволен, по договорённости с членами группы, которая может формироваться произвольно. Варианты самостоятельной работы можно составить различными по степени трудности для учёта индивидуальных особенностей учащихся. На уроке предусмотрена работа в парах и группах. Объём выполненной работы на уроке и степень самостоятельности оценивается учителем по рабочему листу ученика.

Необходимые для выполнения на уроке задания разнообразны по форме подачи условия (текст, лото, тест, игровые моменты), позволяют развивать творческую и мыслительную деятельность учащихся сформировать:

·           Умение применить знания на практике

·           Умения чётко и ясно излагать свои мысли

I. Организационный момент.

Сегодня мы заканчиваем изучение темы "Интеграл". Мы познакомились с понятием интеграл, узнали о его применении для вычисления площадей фигур. На сегодняшнем уроке мы ещё раз пролистаем страницы применения этого математического понятия. А также научимся вычислять определенный интеграл с помощью компьютерных программ.

II. Актуализация знаний

Карточка №1 Найти пары чисел а и в, при которых функция f(x) удовлетворяет условиям

f(x)= ах² –в, = 6, f ' (3) = 48

Решение:

f ' (x)=2ах; 6а = 48; а = 8,

===

=6, в=18

Карточка №2 Вычислить интеграл, используя его геометрический смысл.

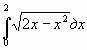
Решение: у=,

у 0

у² =2х – х² , (х-1)² + у² =1

Это уравнение окружности с центром (1;0) и радиусом R=1. Площадь круга данного радиуса S_кр = R²= . Учитывая, что у 0

= =

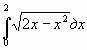Карточка №3

При каком значении а (1/2< а <18) S₁S₂ ?

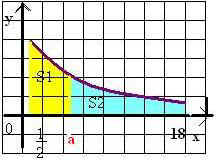
Решение:

S₁=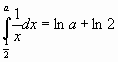

S₂₌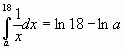

По условию S₁ S_{2 ,} значит lna+ln2 ln18-lna _,

2 lna 9; а² 9; -3 а 3

Учитывая условие 1/2< а <18, получаем 1/2< а <3.

1.         Как вы считаете, что нужно знать, чтобы вычислить площади фигур?

2.         Дайте определение первообразной функции, неопределенного интеграла.

Дайте определение определенного интеграла. Запишите формулу, по которой он вычисляется? Чье имя носит эта формула? (Можно сообщить заранее подготовленную историческую справку о И. Ньютоне и Г. Лейбнице. (см. Слайд 1 – слайд демонстрируется на компьютере, дфомируется с помощью MS Power Point)

Предложите способ вычисления указанных интегралов (устно) (Слайд 2).

Задание 2 Вычисление определенного интеграла с помощью таблицы Excel. Данное задание дается с целью уяснения учащимися сущность метода численного решения задачи и овладеть первичными навыками составления, ввода, трансляции, отладки, исполнения и оформления задачи в табличном редакторе.

Для численного вычисления определенного интеграла методом трапеций используется формула:

Методику вычисления определенного интеграла в Excel с использованием приведенной формулы рассмотрим на примере.

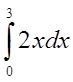
Пусть требуется вычислить определенный интеграл

Величина интеграла, вычисленная аналитически равна 9. Для численного вычисления величины интеграла с использованием приведенной формулы выполните следующие действия:

-    табулируйте подинтегральную функцию в диапазоне изменения значений аргумента 0 – 3 (см. рис.).

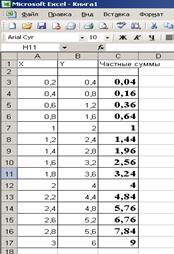
-    в ячейку С3 введите формулу =(A3-A2)*B2+(A3-A2)*(B3-B2)/2+C2, которая реализует подинтегральную функцию.

-    Скопируйте буксировкой формулу, записанную в ячейке С3 до значения аргумента х = 3. Вычисленное значение в ячейке С17 и будет величиной заданного интеграла - 9.

Вычислите интегралы, работая парами. Выбирая соответствующую ответу букву, вы прочтете фамилию французского математика, который дал определение интеграла как предела интегральных сумм. (ответ: Огюстен Луи Коши. 1789-1857).

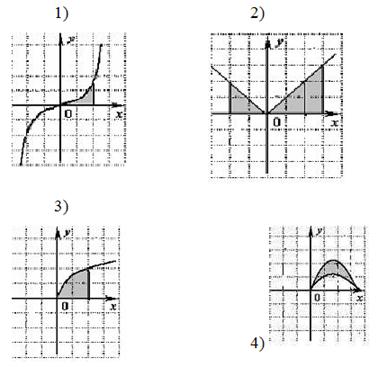
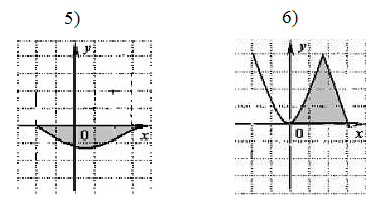
Дайте определение криволинейной трапеции (Слайд 3). Среди фигур, изображенных на рисунке, выбрать криволинейную трапецию. /Ответ:1,3,5/

Вспомните, как вычисляется площадь криволинейной трапеции. Запишите формулу для площади. Как можно вычислить площади фигур в случаях 2,4,6?

Работа в группах (по 4 человека) Задание: вычислить площади криволинейных трапеций – игра "Лото". (см. Слайд 4).

Справившиеся с заданиями учащиеся могут приступить к выполнению заданий IV и V в рабочем листе урока.

Задание IV. Вычислить площадь фигуры, ограниченной графиком функции

у=|-х²-4х -3|, осью ОХ.

Решение: -х²-4х -3 0, координаты вершины х₀ = -2;у₀ =1

Площадь заштрихованной фигуры

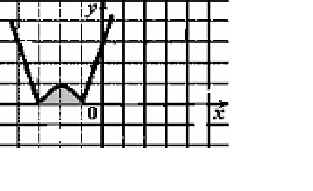
S= 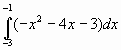= -(=1

Задание V.

При каком значении а числа S_1, S₂, S₃ образуют три последовательных числа арифметической прогрессии. Найти разность этой прогрессии.

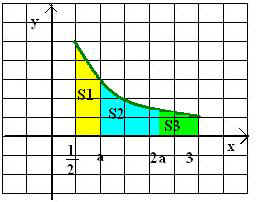
Решение:

S₁ =2 -

S₂ = -

S₃ = -

Согласно свойству арифметической прогрессии

2S₂ = S₁+ S_3, т.е.

2( - )= 2 - + - ; =; а=

S₁=; S₂ =

Разность прогрессии

d= S₂ - S₁ =-

Подведение итогов урока. Выяснить наличие вопросов, которые появились при решении рассмотренных на уроке задач, а также учитель просит ребят оценить свою работу на уроке, на сколько она была плодотворной, что было на уроке удачным, а что нет.

Слайд 1 - Познай секреты математики:

"Интеграл. Вычисление площадей с помощью определённого интеграла"

I.    "Закодируй ответ"

II.   Определите фамилию французского математика, который дал определение определенного интеграла как предела интегральных сумм.

"Да, много решено загадок

от прадеда и до отца,

и нам с тобой продолжить надо

тропу, которой нет конца"

(В. Ноздрёв, профессор)

III.       "Лото" Вычисли площадь криволинейных трапеций.

IV.Вычислите площадь фигуры, ограниченной графиком функции

у=|-х² - 4х-3| и осью ОХ.(рисунок)

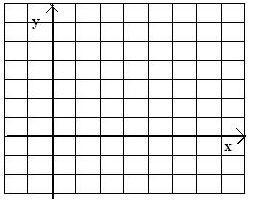
V.  При каком значении а числа S_1, S_2, S₃ образуют три последовательных члена арифметической прогрессии. Найти разность этой прогрессии.<рисунок>

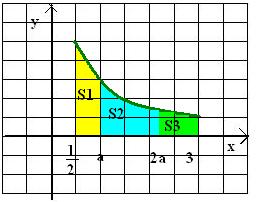
Слайд 2

1. (ответ: 1/4)

2. (ответ )

3. 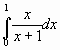(ответ: 1-ln2)

4. (ответ: 2+ln3)

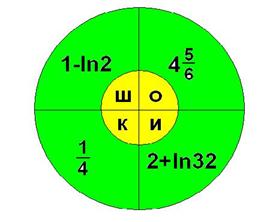
можно расположить за "шторкой" на интерактивной доске. После обсуждения методов решения, "шторку" открыть.

Слайд 3

Слайд 4

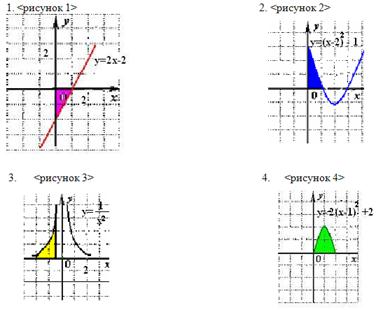
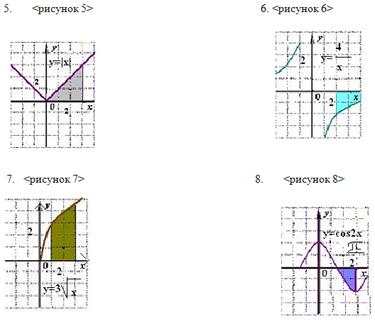
Ответы к Слайду 4

1)         1

2)         1

3)         2

4)        

5)         4,5

6)         4ln2

7)         6-2

8)         0,5

1	1	2
4,5	4ln2	6-2	0,5

Правила игры "Лото". Учитель готовит 5-6 больших карт, разделенных на прямоугольники с записанными на них ответами, и соответственное количество карточек с примерами. Большие карты раздаются группам играющих. Дается время, в течение которого ребята, разделив по своему усмотрению карточки, выполняют задания (можно всей группе решать одно и то же задание, затем сверять). Найдя на большой карте ответ, который считает правильным группа, накрывают им задание. Выигрывает та группа, которая раньше всех накрыла все клетки своих карт. Чтобы проверить правильность решения, учитель переворачивает карточки и тогда, если все ответы верны, должна получиться картинка, которую предварительно рисуют на всех маленьких карточках (сначала рисуют картинку, потом пишут задания, а затем их разрезают).

Урок 3

Интегрированный урок (физика + математика) по теме "Применение интеграла при решении физических задач"

Цель: продолжить формирование умений самостоятельно в комплексе применять знания, умения и навыки, осуществлять их перенос в новые условия.

Задачи:

Обучающие: способствовать формированию знаний, умений по данной теме;

Развивающие: умственная деятельность (выполнять операции анализа, синтеза, делать выводы, выделять существенные признаки объектов);

Воспитательные: воспитывать умение организовать свою деятельность, формирование ценностной ориентации, мировоззрения.

Оборудование: компьютер, мультимедиа проектор, экран.

Содержание урока: данного урока нет в тематическом планировании, но нами предлагается использовать данную разработку изучении темы 7.

План урока:

1.         Организация начала урока.

2.         Постановка проблемы урока.

3.         Актуализация ЗУН, необходимых для творческого применения знаний

4.         Формирование новых понятий и способов действий

5.         Подведение итогов урока

Ход урока:

1.         Организация начала урока.

2.         Постановка проблемы урока. На прошлом уроке мы ознакомились с геометрическими задачами, которые решаются при помощи интеграла. Но интеграл применим не только в математике, другие области науки также используют его и сегодня мы с вами проверим это на примере такой науки как физика.