Навигация
Восьмеричная система счисления
2.1.2.3 Восьмеричная система счисления
Основание системы q = 8. Для записи чисел используется восемь цифр от 0 до 7. В силу того что основание восьмеричной системы является третьей степенью числа 2, то для представления одного восьмеричного разряда требуется три значащих двоичных разряда (триада). Таким образом, для записи чисел в восьмеричной системе счисления требуется в 3 раза меньше разрядов, чем в двоичной системе (табл. 2.1).
Восьмеричная система счисления играет в ЭВМ вспомогательную роль и используется для компактной записи двоичных кодов чисел машинных команд ЭВМ в различных периферийных устройствах и устройствах подготовки данных. Перевод чисел из двоичной системы счисления в восьмеричную и наоборот осуществляется по триадам согласно второму столбцу таблицы 2.1 (первые восемь строк, неполные триады дополняются слева незначащими нулями). Разбиение двоичного числа на триады осуществляется влево и вправо от запятой, отделяющей целую часть числа от дробной. Если крайние триады получаются неполными, то они дополняются нулями.
Пример.
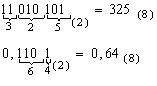
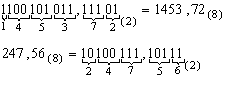
2.1.2.4 Шестнадцатеричная система счисления
Основание системы q = 24 = 16. Для записи чисел исполь-зуются шестнадцать цифр, из них первые десять - известные цифры от 0 до 9. В качестве дополненных цифр используются заглавные латинские буквы A, B, C, D, E и F (табл. 2.1).
Назначение шестнадцатеричной системы счисления аналогично восьмеричной: компактная запись двоичных кодов чисел и команд. Одному шестнадцатеричному разряду числа соответствует четыре двоичных разряда (тетрада), т. е. шестнадцатеричная система позволяет сократить длину записи числа по сравнению с двоичной в 4 раза.
Перевод чисел из двоичной системы в шестнадцатеричную систему и обратно осуществляется по тетрадам аналогично двоично-восьмеричному переводу (табл.2.1). Неполные тетрады дополняются нулями.
Пример.
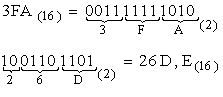
2.1.3 Элементы математической логики
Для описания логики функционирования аппаратных и программных средств ЭВМ используется алгебра логики, или булева алгебра (по имени ее создателя Дж. Буля).
Булева алгебра оперирует с логическими переменными, которые могут принимать только два значения: истина или ложь, обозначаемые соответственно 1 и 0. Как отмечалось выше, основной системой счисления в ЭВМ является двоичная система, в которой также используются цифры 1 и 0. Таким образом, одни и те же устройства ЭВМ могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных. Это обусловливает сравнительную простоту схемной реализации процесса обработки информации в ЭВМ.
Совокупность значений логических переменных x1, x2, ..., xn называется набором переменных.
Набор логических переменных удобно изображать в виде n-разрядного двоичного числа, каждый разряд которого равен значению одной из переменных. Из таблицы 2.1 видно, что количество возможных наборов в n двоичных разрядах равно 2n.
Логической функцией от набора логических переменных (аргументов) f(x1, x2 ..., xn) называется функция, принимающая только два значения: истина или ложь.
Область определения логической функции конечна и зависит от числа возможных наборов аргументов. Любая логическая функция может быть задана с помощью таблицы истинности, где в левой части записываются возможные наборы аргументов, а в правой - соответствующие им функции.
В случае большого числа аргументов табличный способ задания логической функции становится громоздким и теряет наглядность. Так, уже для шести логических аргументов понадобится таблица в 64 строки, поэтому логические функции удобно выражать через другие более простые логические функции одной или двух переменных, описываемые с помощью простых таблиц.
Совокупности таких элементарных логических функций (или логических операций), с помощью которых можно выразить логическую функцию любой сложности, называются функционально полными системами логических функций.
В этой системе определены три элементарные логические операции: инверсия (отрицание), конъюнкция (логическое умножение) и дизъюнкция (логическое сложение).
Логические переменные, объединенные знаками логических операций, составляют логические выражения.
При вычислении значения логического выражения определено следующее старшинство выполнения логических операций: сначала выполняется инверсия, затем конъюнкция и в последнюю очередь - дизъюнкция.
Для изменения указанного порядка используются скобки.
В алгебре логики выполняются следующие основные законы, позволяющие производить тождественные преобразования логи-ческих выражений.
1. Коммутативный закон: x1 Vx2 = x2 V x1,
x1 ×x2 = x2 ×x1.
2. Ассоциативный закон: x1 V (x2 V x3) = (x1 V x2) V x3,
x1 ×(x2 ×x3) = (x1 × x2)× x3.
3. Дистрибутивный закон: x1 × (x2 V x3) = x1 × x2 V x1 × x3.
4. Правила де Моргана (теорема двойственности).
5. Правила операций с константами 0 и 1.
6. Правила операций с переменной и ее инверсией.
7. Закон поглощения.
8. Закон идемпотентности.
9. Закон двойного отрицания.
2.1.4 Методы перевода чисел из одной системы счисления
в другую
2.1.4.1 Метод прямого замещения
Перевод чисел из двоичной системы счисления в систему с основанием, являющимся степенью числа 2, и наоборот не вызывает трудностей. Это в частности стало причиной широкого применения в ЭВМ восьмеричной и шестнадцатеричной систем счисления. Однако может возникнуть задача перевода чисел из одной системы счисления в другую с произвольными основаниями. В этом случае необходимо воспользоваться общими правилами перевода, которые основаны на определении однородной позиционной системы счисления (2.1).
Число в системе счисления с основанием q1 расписывается по формуле (2.1) и вычисляется сумма ряда, при этом арифметические действия выполняются по правилам системы счисления с основа-нием q2.
Следуя этому правилу, легко перевести числа из двоичной и восьмеричной систем счисления в десятичную.
Пример.
![]()
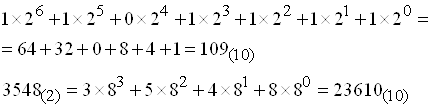
Можно также в отличие от ранее рассмотренного метода перевести числа из двоичной системы в восьмеричную, но для этого необходимо вычислять сумму ряда (2.1) по правилам восьмеричной арифметики. При переводе больших двоичных чисел в десятичные для его упрощения, целесообразно сначала перевести их по триадам в восьмеричные, а затем из восьмеричных в десятичные.
Пример.
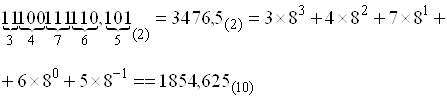
Похожие работы
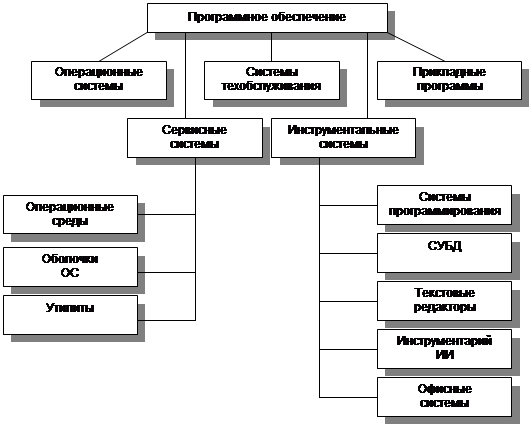
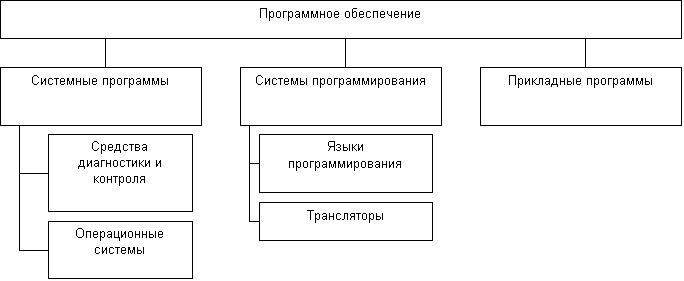
... вычислительной техники, а также принципы функционирования этих средств и методы управления ими. Из этого определения видно, что информатика очень близка к технологии, поэтому ее предмет нередко называют информационной технологией. Предмет информатики составляют следующие понятия: а) аппаратное обеспечение средств вычислительной техники; б) программное обеспечение средств вычислительной техники ...
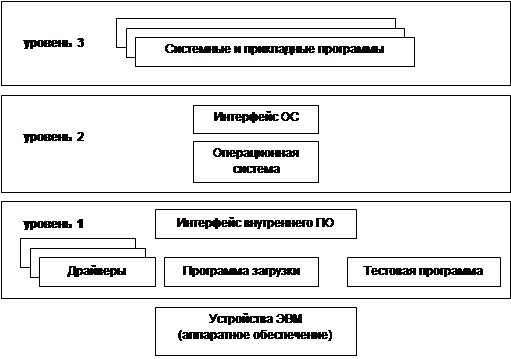
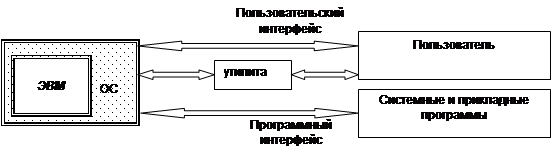
... – набор утилит и некоторые инструментальные программы (пользовательский интерфейс). К третьему уровню относятся все остальные программы. Программы второго и третьего уровней хранятся в файлах. Программное обеспечение первого уровня является машинно-зависимым [computer-independent]. То есть для каждого микропроцессора или семейства ЭВМ набор данных программ уникален. Операционная система имеет ...
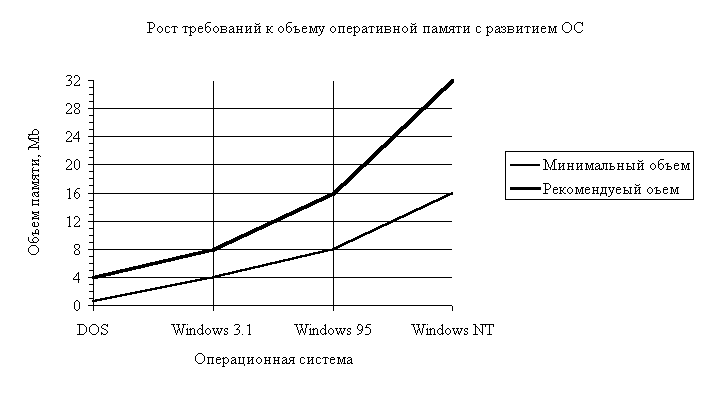
... Вы сможете работать на своем компьютере. От выбора ОС зависят также производительность вашей работы, степень защиты Ваших данных, необходимые аппаратные средства и т.д. [9] 5. Персональная ЭВМ: развернутая структура; структура программного обеспечения; выбор ПЭВМ (если возможно, то по прайс-листу некоторой фирмы). Развернутая структура (тонкие линии показывают управляющие связи, толстые – ...
... » (Zero Administration Initiative), которая будет реализована во всех следующих версиях Windows. SMS- сервер управления системами У SMS две задачи — централизовать управление сетью и упростить распространение программного обеспечения и его модернизацию на клиентских системах. SMS подойдет и малой, и большой сети — это инструмент управления сетью на базе Windows NT, эффективно использующий ...

0 комментариев