Навигация
Построение и использование имитационных моделей
33111
знаков
13
таблиц
37
изображений
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ, МЕХАНИКИ И ОПТИКИ
Кафедра компьютерных образовательных технологий
КУРСОВАЯ РАБОТА
Тема: Построение и использование имитационных моделей
Работу выполнил студент
Машков Андрей Сергеевич
Техническое задание
1. Наименование темы: Построение и исследование имитационных моделей
2. Срок сдачи студентом законченной работы 05.06.07
3. Техническое задание и исходные данные к работе Разработать программу для имитационного моделирования системы массового обслуживания с 2 устройствами. В системе интервалы времени между поступлением требований являются независимыми случайными величинами со средним временем поступления требований 
=10 (с). Когда требование поступает, а устройство свободно, обслуживание начинается немедленно. Время обслуживания является случайной величиной некоррелированной с интервалами поступления требований. Среднее значение времени обслуживания требований 
=10 (c). Если при поступлении требования устройства заняты, требование становится в очередь.
Дисциплина обслуживания: циклическая с квантом q=1c.
Оценке подлежат следующие параметры:
· коэффициент использования системы 
;
· средняя задержка в очереди 
;
· среднее время ожидания 
;
· среднее по времени число требований в очереди 
;
· среднее по времени число требований в системе 
.
4. Содержание курсовой работы (перечень подлежащих разработке вопросов):
· Анализ задачи и обзор аналогов;
· Выбор входных распределений;
· Логика работы программы;
· Построение генераторов случайных чисел;
· Статистический анализ выходных данных моделирования;
· Рекомендации по использованию результатов моделирования.
5. Перечень графического материала (с указанием обязательного материала):
· Графики функций распределения вероятностей;
· Графики функций плотности распределения вероятностей;
· График по времени числа требований в очереди;
· График по времени числа требований в системе;
· График по времени коэффициента использования системы;
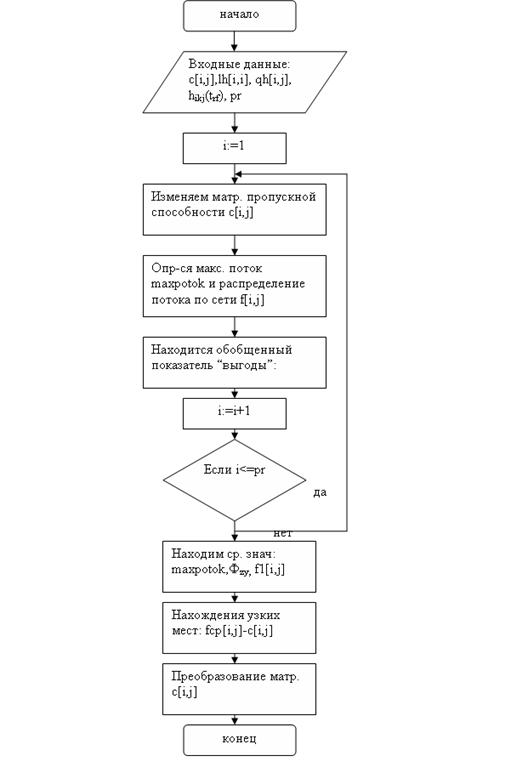
· Блок-схемы алгоритмов.
6. Исходные материалы и пособия
1. Кельтон В., Лоу А. Имитационное моделирование. Классика CS. 3-ие изд. – СПб.:Питер; Киев: Издательская группа BHV, 2004. – 847 c.
Содержание
Введение
1. Анализ задачи и обзор аналогов
2. Выбор входных распределений. Построение генераторов случайных чисел
3. Оценка входных параметров
3.1 Оценки средних значений
3.2 Интервальные оценки
3.3 Проверка статистических гипотез
3.4 Метод гистограмм
4. Логика работы программы
4.1 Блок-схема алгоритма программы
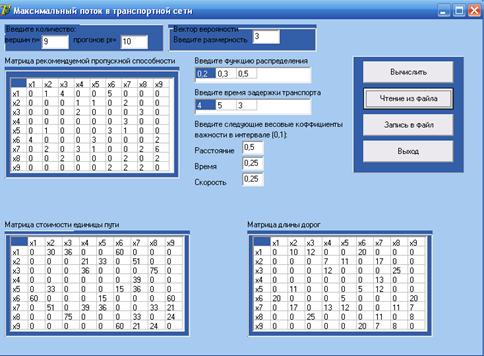
4.2 Интерфейс
5. Планирование эксперимента
5.1 Статический анализ выходных данных моделирования
5.2 Построение факторного плана
5.3 Эффекты взаимодействия и уравнения регрессии
6. Рекомендации по использованию результатов моделирования
Заключение
Приложение А
Приложение Б
Список литературы
Введение
На производстве, в быту, военном деле, науке и т. д. часто встречаются процессы, которые, не вдаваясь в детали, можно описать следующим образом: с одной стороны, постоянно возникают запросы на выполнение каких-либо работ, а с другой — происходит постоянное удовлетворение этих запросов. Та часть процесса, в которой возникают запросы, называется обслуживаемой системой, а та, которая принимает запросы и удовлетворяет их,— обслуживающей. Совокупность обслуживающей и обслуживаемой систем составляет систему массового обслуживания. Под системой массового обслуживания (СМО) понимают динамическую систему, предназначенную для эффективного облуживания случайного потока требований при ограниченных ресурсах системы.
Модели системы массового обслуживания являются наиболее часто используемым классом моделей со случайными факторами, что определяется повсеместным распространением систем такого типа.
К настоящему времени разработано много моделей систем массового обслуживания, имеющих аналитическое решение. Но они далеко не исчерпывают все способы функционирования реальных обслуживающих систем. Кроме того, на практике не всегда выполняются предпосылки, лежащие в основе имеющихся аналитических моделей.
Основной задачей теории СМО является изучение режима функционирования обслуживающей системы и исследование явлений, возникающих в процессе обслуживания.
Задачи теории массового обслуживания носят оптимизационный характер и в конечном итоге включают экономический аспект по определению такого варианта системы, при котором будет обеспечен минимум суммарных затрат от ожидания обслуживания, потерь времени и ресурсов на обслуживание и простоев каналов обслуживания.
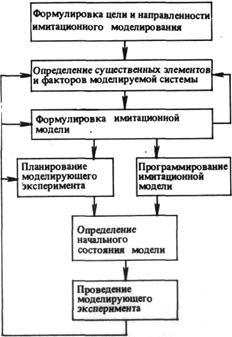
Эффективным методом решения задач теории массового обслуживания, как и многих других, не имеющих аналитического решения, является метод статистического моделирования, предусматривающий, имитацию на ЭВМ процессов, протекающих в исследуемой системе. Математическое описание процесса в этом случае задается алгоритмически. Моделирующий алгоритм многократно воспроизводит изучаемый случайный процесс, накапливает сведения о его протекании, и после обработки выдает оценки показателей работы системы. Целью любого компьютерного эксперимента является сбор информации о значениях переменных модели, наблюдаемых в процессе проведения эксперимента, и состояниях очередей, возникающих в процессе моделирования.
Построение программы имитации поведения СМО основано на программировании цепочки событий, начиная от входных требований, поступающих в случайные моменты времени, занятия и освобождения серверов в соответствии со случайным характером длительности обработки каждого требования. Итогом работы программы является получение статистических отчетов о процессах в системе.
В данной курсовой работе требуется разработать программу для имитационного моделирования системы массового обслуживания с двумя устройствами. В системе интервалы времени между поступлениями требований являются независимыми случайными величинами со средним временем Ā = 10 секунд. Когда требование поступает, а устройство свободно, обслуживание начинается немедленно. Время обслуживания является случайной величиной, некоррелированной с интервалами поступления требований. Среднее значение обслуживания требований – Ŝ = 10 секунд. Если при поступлении требования устройства заняты, то требование становится в очередь. Дисциплина обслуживания циклическая с квантом q=1c.
Оценке подлежат следующие параметры:
· коэффициент использования системы;
· средняя задержка в очереди;
· среднее время ожидания;
· среднее по времени число требований в очереди;
· среднее по времени число требований в системе.
Похожие работы
... построения компьютерной модели o Построение алгоритма решения задачи и его кодирование на одном из языков программирования; o Построение компьютерной модели с использованием одного из приложений (электронных таблиц, СУБД и пр.) 4 этап – компьютерный эксперимент o Если компьютерная модель существует в виде программы на одном из языков программирования, её нужно запустить на выполнение ...
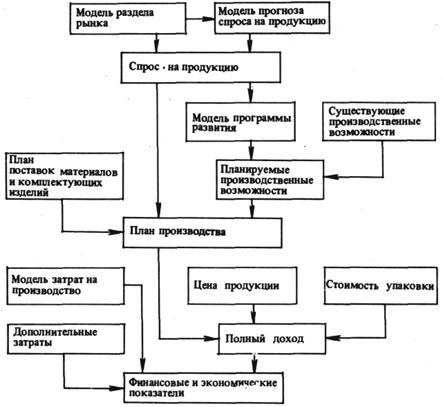
... операции сборки имитируются аналогично операциям обработки – определяются случайные или детерминированные затраты времени на операцию, значения физических и производственных характеристик. 3. Имитационные модели предприятий и производственных объединений Для имитации сложных производственных систем требуется создание логико-математической модели исследуемой системы, позволяющей проведение ...
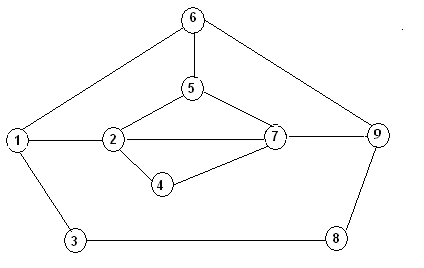
... ; решение тестовых задач с помощью имитационной. Таким образом, был разобран материал по данной курсовой работе и выявлена актуальность разработки имитационной модели транспортной сети и выполнено программное обеспечение, реализующее работу модели железнодорожной сети. Данная модель разработана для случая одного входа и одного выход в сеть и нуждается в дополнительной модификации программы, что ...
Стратегическое планирование жилищного фонда Субъекта Федерации с использованием имитационных моделей
... за 1 год. Модель развития жилищного фонда Субъекта Федерации. Динамика развития жилищного фонда города описывается следующими уравнениями ; ; ; ; . Как видно из модели, скорость изменения общей площади жилищного фонда Субъекта Федерации G зависит от темпов ввода жилья и вывода его из эксплуатации . В свою очередь, параметр согласно приведенным уравнениям обусловлен темпами ввода в ...
0 комментариев