Навигация
Эффекты взаимодействия и уравнения регрессии
5.3 Эффекты взаимодействия и уравнения регрессии
Главные эффекты первого, второго и третьего факторов вычисляются по следующим формулам:
![]() ,
,
![]() , (5.2)
, (5.2)
![]() ,
,
где ![]() – отклики системы.
– отклики системы.
Эффекты взаимодействия первого и второго, первого и третьего, второго и третьего, первого и второго и третьего факторов вычисляются по следующим формулам:
![]() ,
,
![]() , (5.3)
, (5.3)
![]() ,
,
![]() ,
,
где ![]() – отклики системы.
– отклики системы.
Значения эффектов для каждого выходного параметра представлены в таблице 5.4.
Таблица 5.4 – Значения эффектов
| Параметр | e1 | e2 | e3 | e12 | e13 | e23 | e123 |
| p | -0,3192115 | -0,0686965 | 0,06653 | -0,6994355 | -0,642834 | -0,0686965 | 0,062186 |
| d | -18,315773 | -3,1235475 | 3,5655875 | -25,774998 | -25,052413 | -3,1235475 | 0,4575825 |
| w | -18,15955 | -3,30525 | 4,48465 | -34,1838 | -32,7314 | -3,30525 | 0,5327 |
| Q | -1,5063818 | -0,424687 | 0,3191838 | -1,7749518 | -1,7066363 | -0,4246868 | 0,10430775 |
| L | -1,1264325 | -0,556723 | 0,4529075 | -2,6504325 | -2,4088725 | -0,5567225 | 0,1591375 |
Общий вид уравнения регрессии представлен ниже:
![]() , (5.4)
, (5.4)
где ![]() - коэффициенты уравнения регрессии.
- коэффициенты уравнения регрессии.
Значения коэффициентов уравнения регрессии представлены в таблице 5.5. Пример вычисления коэффициентов представлен в приложении Б.
Значения коэффициентов уравнения регрессии представлены в таблице 5.5.
Таблица 5.5 – Значения коэффициентов уравнения регрессии
| Ρ | d | W | Q | L |
| -43,2915 | -235,808 | -45,0088 | -59,9977 | -85,6907 |
| 24,04419 | 144,1403 | 66,1593 | 36,02849 | 57,9095 |
| 3,770473 | 15,9089 | 0,5527 | 4,668797 | 6,93938 |
| 5,335393 | 47,84272 | 27,3329 | 9,391359 | 12,49551 |
| -2,09804 | -10,2775 | -4,1604 | -2,86784 | -4,8038 |
| -0,45454 | -3,17093 | -1,445 | -0,71899 | -0,98899 |
| -2,88832 | -26,2564 | -17,3224 | -5,33401 | -7,76647 |
| 0,248744 | 1,83033 | 1,1306 | 0,417231 | 0,63655 |
Уравнения регрессии для каждого из откликов:
ρ = - 43.2915 + 24.04419m + 3.770473![]() + 5.335393
+ 5.335393![]() - 2.09804
- 2.09804![]() - 0.45454
- 0.45454![]()
![]() - 2.88832m
- 2.88832m![]() + 0.248744m
+ 0.248744m![]()
![]() ;
;
d = - 235.808 + 144.1403m + 15.9089![]() + 47.84272
+ 47.84272![]() - 10,2775m
- 10,2775m![]() - 3.17093
- 3.17093![]()
![]() - 26.2564m
- 26.2564m![]() + 1.83033m
+ 1.83033m![]()
![]() ;
;
w = - 45.0088+ 66.1593m + 0.5527![]() + 273329
+ 273329![]() - 4.1604m
- 4.1604m![]() - 1.445
- 1.445![]()
![]() - 17.3224m
- 17.3224m![]() + 1.1306m
+ 1.1306m![]()
![]() ;
;
Q= - 59.9977 + 36.02849m + 4.668797![]() + 9.391359
+ 9.391359![]() - 2.86784m
- 2.86784m![]() - 0.71899
- 0.71899![]()
![]() - 5.33401m
- 5.33401m![]() + 0.417231m
+ 0.417231m![]()
![]() ;
;
l = -85.6907 + 57.9095m + 6.93938![]() + 12.49551
+ 12.49551![]() - 4.8038m
- 4.8038m![]() - 0.98889
- 0.98889![]()
![]() - 7.76647m
- 7.76647m![]() + 0.63655m
+ 0.63655m![]()
![]() .
.
По уравнениям регрессии для значения для входных параметров m=2, ![]() =10,
=10, ![]() =10 получаем:
=10 получаем:
ρ = 0.4231; d =8.2874; w = 18.1298; Q = 0.1710; l =1.4828.
Для проверки адекватности уравнений регрессии используем метод малых приращений. Так, для значений m, ![]() ,
, ![]() значения были получены выше. В таблице 5.6 представлены результаты при малом приращении с (dm = 0,04),
значения были получены выше. В таблице 5.6 представлены результаты при малом приращении с (dm = 0,04), ![]() (d
(d![]() = 0,2),
= 0,2),![]() (d
(d![]() =0,2):
=0,2):
Таблица 5.6 – Метод малых приращений
| N | Dm | d | d | Ρ | d | w | Q | L |
| 1 | 0 | 0 | 0 | 0.4231 | 8.2874 | 18.1298 | 0.1710 | 1.4828 |
| 2 | -0,04 | 0 | 0 | 0.4609 | 9.8100 | 19.5541 | 0.3417 | 1.6483 |
| 3 | 0,04 | 0 | 0 | 0.3853 | 6.7568 | 16.7055 | 0.0003 | 1.3173 |
| 4 | 0 | -0,2 | 0 | 0.4223 | 8.2331 | 18.0510 | 0.1535 | 1.4482 |
| 5 | 0 | 0,2 | 0 | 0.4239 | 8.3336 | 18.2086 | 0.1886 | 1.5174 |
| 6 | 0 | 0 | -0,2 | 0.4255 | 8.2380 | 17.9598 | 0.1954 | 1.5221 |
| 7 | 0 | 0 | 0,2 | 0.4208 | 8.3288 | 18.2998 | 0.1466 | 1.4435 |
Похожие работы
... построения компьютерной модели o Построение алгоритма решения задачи и его кодирование на одном из языков программирования; o Построение компьютерной модели с использованием одного из приложений (электронных таблиц, СУБД и пр.) 4 этап – компьютерный эксперимент o Если компьютерная модель существует в виде программы на одном из языков программирования, её нужно запустить на выполнение ...
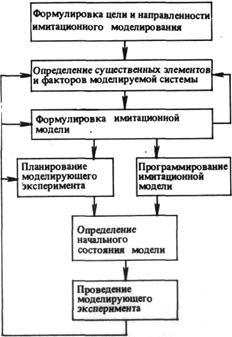
... операции сборки имитируются аналогично операциям обработки – определяются случайные или детерминированные затраты времени на операцию, значения физических и производственных характеристик. 3. Имитационные модели предприятий и производственных объединений Для имитации сложных производственных систем требуется создание логико-математической модели исследуемой системы, позволяющей проведение ...
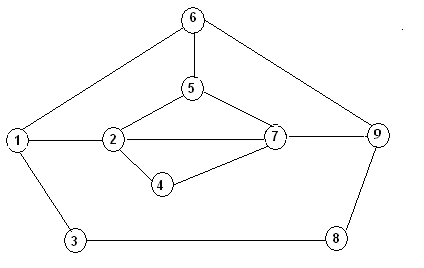
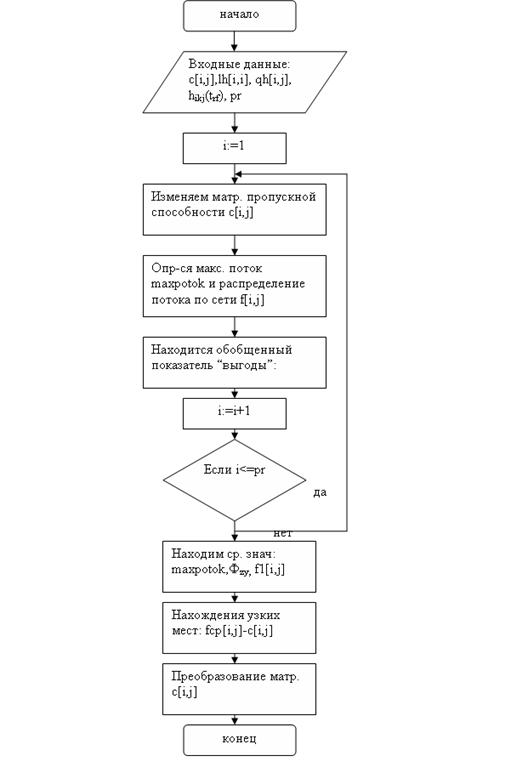
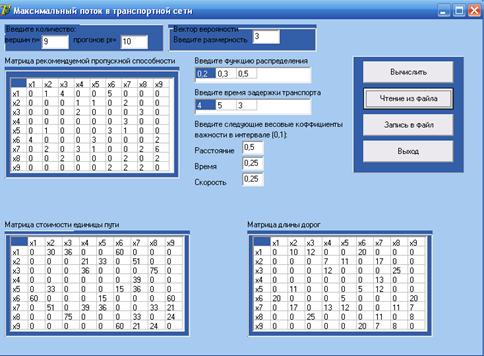
... ; решение тестовых задач с помощью имитационной. Таким образом, был разобран материал по данной курсовой работе и выявлена актуальность разработки имитационной модели транспортной сети и выполнено программное обеспечение, реализующее работу модели железнодорожной сети. Данная модель разработана для случая одного входа и одного выход в сеть и нуждается в дополнительной модификации программы, что ...
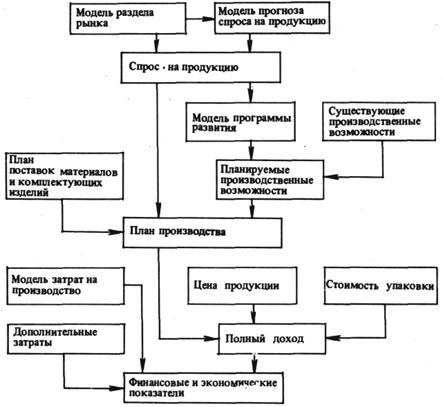
... за 1 год. Модель развития жилищного фонда Субъекта Федерации. Динамика развития жилищного фонда города описывается следующими уравнениями ; ; ; ; . Как видно из модели, скорость изменения общей площади жилищного фонда Субъекта Федерации G зависит от темпов ввода жилья и вывода его из эксплуатации . В свою очередь, параметр согласно приведенным уравнениям обусловлен темпами ввода в ...


0 комментариев