Навигация
4.2 Интерфейс
К графическому интерфейсу относится управление параметрами системы, такими как изменение входных параметров.
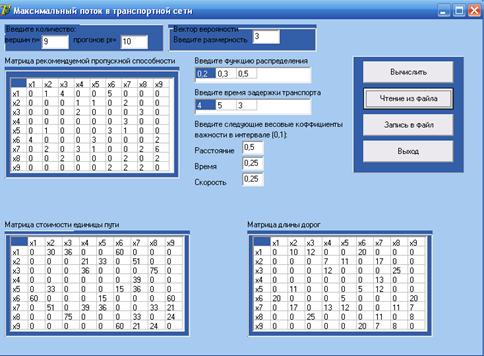
На рисунке 4.5 представлено основное диалоговое окно графического интерфейса.
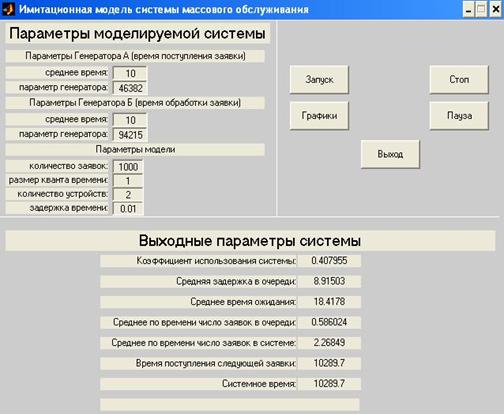
Рисунок 4.5 - Основное диалоговое окно графического интерфейса
Здесь имеются поля для ввода входных параметров, кнопки управления происходящим процессом.
При нажатии на клавишу «Запуск» мы видим диалоговое окно, представленное на рисунке 4.6. Здесь можно заметить, что поля ввода входных параметров неактивны для изменения. Так же в графе «Выходные параметры системы» результаты показываются только по двум пунктам: системное время и время поступления следующей заявки. Кнопка «Графики» неактивна. Соответственно происходит выполнение работы программы.
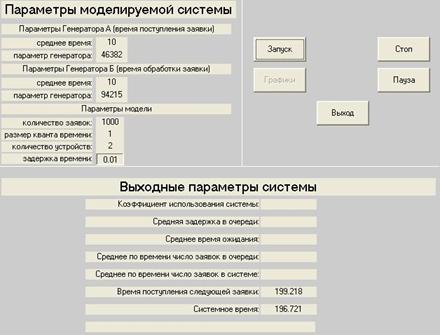
Рисунок 4.5 – Диалоговое окно при нажатии на кнопку «Запуск»
При нажатии на кнопку «Стоп» происходит активация полей ввода «Параметры моделируемой системы». Так же выводится информация о промежуточных подсчётах. Можно посмотреть полученные графики. Это можно посмотреть на рисунке 4.6.
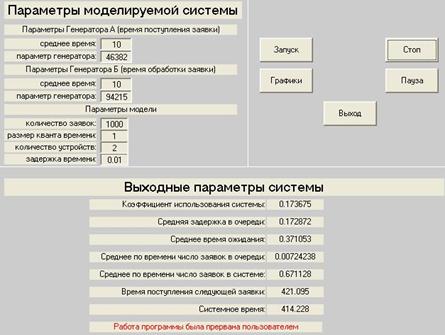
Рисунок 4.6 - Диалоговое окно при нажатии на кнопку «Стоп»
После окончательного прогона моделирования системы массового обслуживания и нажатия на кнопку «Графики» мы увидим:
· график изменения коэффициента использования системы во времени на рисунке 4.7;
· график текущего по времени числа заявок в очереди на рисунке 4.8;
· график текущего по времени числа заявок в системе на рисунке 4.9;
· график среднего по времени числа заявок в очереди и системе на рисунке 4.10.
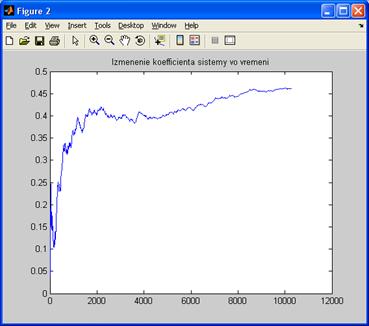
Рисунок 4.7 - Изменения коэффициента использования системы во времени
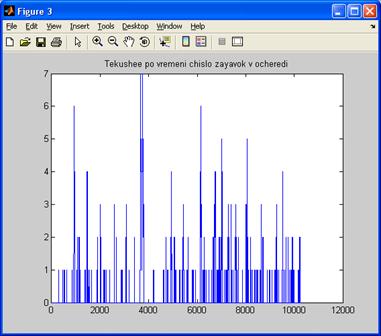
Рисунок 4.8 - Текущее по времени число заявок в очереди
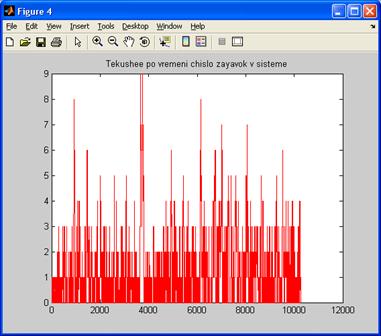
Рисунок 4.9 - Текущее по времени число заявок в системе
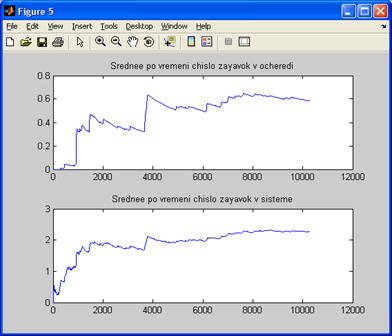
Рисунок 4.10 - Среднего по времени числа заявок в очереди и системе
5 Планирование эксперимента
5.1 Статический анализ выходных данных моделирования
Для анализа выходных параметров моделирования необходимо рассчитать количество экспериментов для построения факторного плана. Расчет количества экспериментов производится по формуле:
, (5.1)
где 
- дисперсия, 
- 5% от математического ожидания на 10 значениях каждого выходного параметра, 
=1.96 – квантиль порядка 
.
Результаты расчетов необходимого количества экспериментов приведены в таблице 5.1.
Таблица 5.1 – Количество экспериментов
| A1 | S1 | p | d | w | Q | L | |
| 1 | 254789 | 251463 | 0,425622 | 9,23302 | 19,0935 | 0,564 | 2,2317 |
| 2 | 62315 | 56514 | 0,42811 | 10,1712 | 20,7671 | 0,609816 | 2,24761 |
| 3 | 54789623 | 1263532 | 0,500968 | 10,0617 | 20,1693 | 0,757584 | 2,54167 |
| 4 | 658765 | 459877 | 0,480135 | 8,99325 | 18,8155 | 0,549471 | 2,24218 |
| 5 | 678678 | 967567 | 0,421836 | 8,863665 | 18,111 | 0,477824 | 2,04563 |
| 6 | 872343 | 976723 | 0,490978 | 8,75354 | 18,384 | 0,53815 | 2,24663 |
| 7 | 98745 | 874509 | 0,476293 | 9,028 | 18,873 | 0,552332 | 2,27674 |
| 8 | 2148963 | 1247896 | 0,482266 | 9,24245 | 19,2856 | 0,534981 | 2,21667 |
| 9 | 2652567 | 4589642 | 0,411253 | 8,32548 | 17,9225 | 0,432992 | 2,0688 |
| 10 | 829192 | 873292 | 0,472514 | 9,23085 | 19,0708 | 0,622302 | 2,36714 |
| n | 8,090238 | 5,737406 | 3,266298 | 37,26833 | 5,93063 |
В таблице 5.1 приняты следующие обозначения: A1 – начальное значение величины A (поступления требования); S1 - начальное значение величины S (обработки требования); p, d, w, Q, L – выходные параметры, соответственно коэффициент использования, системы, средняя задержка в очереди, среднее время ожидания, среднее по времени число требований в очереди, среднее по времени число требований в системе; n – необходимое количество экспериментов вычисленное по формуле 5.1.
Было определено максимальное значение n равное 37.
Похожие работы
... построения компьютерной модели o Построение алгоритма решения задачи и его кодирование на одном из языков программирования; o Построение компьютерной модели с использованием одного из приложений (электронных таблиц, СУБД и пр.) 4 этап – компьютерный эксперимент o Если компьютерная модель существует в виде программы на одном из языков программирования, её нужно запустить на выполнение ...
... операции сборки имитируются аналогично операциям обработки – определяются случайные или детерминированные затраты времени на операцию, значения физических и производственных характеристик. 3. Имитационные модели предприятий и производственных объединений Для имитации сложных производственных систем требуется создание логико-математической модели исследуемой системы, позволяющей проведение ...
... ; решение тестовых задач с помощью имитационной. Таким образом, был разобран материал по данной курсовой работе и выявлена актуальность разработки имитационной модели транспортной сети и выполнено программное обеспечение, реализующее работу модели железнодорожной сети. Данная модель разработана для случая одного входа и одного выход в сеть и нуждается в дополнительной модификации программы, что ...
Стратегическое планирование жилищного фонда Субъекта Федерации с использованием имитационных моделей
... за 1 год. Модель развития жилищного фонда Субъекта Федерации. Динамика развития жилищного фонда города описывается следующими уравнениями ; ; ; ; . Как видно из модели, скорость изменения общей площади жилищного фонда Субъекта Федерации G зависит от темпов ввода жилья и вывода его из эксплуатации . В свою очередь, параметр согласно приведенным уравнениям обусловлен темпами ввода в ...
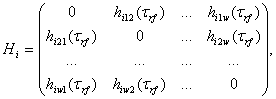
0 комментариев