Событии (нежелательном) состоящем в том, что произошел прогнозируемый сбой;

1. событии (нежелательном) состоящем в том, что произошел прогнозируемый сбой;

2. событии (желательном) состоящем в том, что защита сработает.

Рассмотрим случай, когда оба типа событий характеризуются постоянными интенсивностями (поскольку временные зависимости этих параметров обычно не известны). Пусть:

e – интенсивность (то есть вероятностью возникновения в единицу времени) возникновения ошибки (сбоя);

lr – интенсивностью отказа (не срабатывания) защиты, характеризующая надежность защиты;

ld – интенсивность срабатывания диагностики, характеризующая надежность системы диагностики Pd.

Тогда сомножители, входящие в формулу (А.13), можно представить в следующем виде:

где T – периодичность работы программного модуля;

a, b – вероятности ошибок 1–го и 2–го рода диагностики.

Диагностика представляет собой устройство (или программу), обеспечивающее оповещение оператора о сбое и принятии решения о дальнейшей работе. Исправный диагностический модуль по аналогии с размыкателем характеризуется двумя ошибками: ошибка 1–го рода – ложное срабатывание (например, выключение без наличия сбоя), ошибка 2–го рода – отсутствие срабатывания при наличии сбоя. Защита не эффективна в обоих случаях.

Подстановка (А.13) – (А.15) в (А.12) дает выражение:

,(А.17)

где

.

Функция (А.16) достигает максимума при значении T равном:

(А.18)

Значение T* представляет собой оптимальное время T защищенности программы. Таким образом, этот метод позволяет определить оптимальную периодичность работы программы, при которой защита с заданными характеристиками e, lr, ld дает оптимальный эффект. Либо можно оценить одну из характеристик e, lr, ld при заданных остальных и заданном T*.

Например, оценим T*:

e – один раз в месяц, т.е. равна 3,7e–7;

lr = e;

ld – один раз в минуту, т.е. равен 0,017.

Тогда T* = 59 с.

Теперь, оценим ld при следующих условиях:

T* = 60 с;

e – один раз в год, т.е. равна 3,3e–8;

lr = e.

Тогда из (А.17) имеем

.

Получаем ld = 1,67e–02 1/с или один раз в минуту.

Модель Дюэна

Модель рассмотрена в работе [20]. Эта модель была предложена для оценки роста надежности. Для этого рассматривается отношение интенсивности обнаружения ошибок к общему времени тестирования. В основу модели положены следующие предположения:

обнаружение любой ошибки равновероятно;

общее число ошибок N(t), обнаруженных к произвольному моменту t, распределено по закону Пуассона со средним значением n(t) = a×tb.

Из этого следует, что

.

Из МНК получают следующую оценку для a и b:

,

,

где

Xi = ln(ti), Yi = ln(i/ti),

,

Для использования этой модели требуется только знание моментов времени ti проявления ошибок.

Метод Холстеда оценки числа оставшихся в ПО ошибок

Модель рассмотрена в работе [20]. На сегодняшний момент это единственная модель, с помощью которой можно оценить число ожидаемых (то есть потенциальных) ошибок в ПО еще на этапе составления ТЗ на ПО.

Для программы вводится понятие длины программы N и объем программы (в битах) V:

N = n1×log2n1 + n2×log2n2,

V = N×log2(n1 + n2),(А.19)

где n1 – число различных операций (например, таких как IF, =, DO, PRINT и т.п.); n2 – число различных переменных и констант.

Далее рассматривается потенциальный объем программы (в битах) V*:

,(А.20)

где  – только число входных и выходных переменных.

Величина  может быть выявлена уже на стадии ТЗ или технического проекта на разработку ПО.

Еще вводится понятие уровня программы L, который определяется как отношение потенциального объема V* к объему V:

L = V*/V.

Также вводятся величины:

E = V/L = V2/V*,

l = L×V*

– уровень языка программирования. Значения l для некоторых языков программирования: Ассемблер – 0,88; Фортран – 1,14; PL–1 – 1,53; С/С++ – 1,7; Pascal – 1,8; JAVA – 1,9.

Из этого следует, что

V = (V*)2/l.(А.21)

Оценка времени, затрачиваемое на разработку ПО:

T = E/S = (V*)3/(l×S) (А.22)

где S – параметр Страуда (психофизиологическая характеристика времени, необходимого человеческому мозгу для выполнения элементарной мыслительной операции. S лежит в пределах от 5 до 20 различий в секунду. Холстедом используется значение S = 18, характеризующее процесс программирования как довольно напряженную умственную работу).

Используя (А.21) можно оценить выигрыш во времени разработки при переходе от одного языка программирования l1 к другому языку l2:

.

Например, выигрыш при переходе с C/C++ на JAVA составит около 10%, а с ассемблера на JAVA – 50%.

Основное предположения этой модели:

общее число ожидаемых ошибок N в программе определяется сложностью ее создания (и это верно, за исключением того, что в вышеперечисленные характеристики ПО не входит сложность проектирования, а учитывается только сложность кодирования!).

мозг человека может обработать одновременно и безошибочно 7±2 объектов (гипотеза Миллера).

Тогда, взяв нижнюю границу в 5 объектов и добавив еще один объект, мы получим максимальное число  = 6 различных входных и выходных параметров для потенциально безошибочной программы. Тогда потенциальный объем V0* по (17): V0* = (6+2) ×log2(6+2) = 24 логических бита.

Следовательно, после обработки 24 битов информации на языке программирования человек совершит одну ошибку.

.

Это означает, что на каждые 3000 бит объема V* приходится одна ошибка. Тогда для реального объема ПО из (П1.20) следует, что число ошибок в ПО:

(А.23)

Модель IBM

Модель рассмотрена в работе [20]. Эта модель предназначена для оценки количества вносимых ошибок в сопровождаемом ПО, находящемся в эксплуатации, при его модификации. Модель построена на данных сопровождения 19 версий ОС OS/360 фирмы IBM.

Пусть Mi – число модулей i–ой (новой) версии. Из них

СИМi – число измененных по отношению к предыдущей версии модулей,

НМi – число новых модулей (то есть Мi = Мi–1 + НМi),

МИМi – число многократно измененных и исправленных модулей (10 и более раз),

ИМi – число модулей, в которые внесено менее 10 изменений.

Из практики сопровождения OS/360 и создания ее новых версий были выявлены следующие зависимости:

ИМi = 0,9 × НМi + 0,15 × СИМi

МИМi = 0,15 × ИМi + 0,06 × СИМi.

Число ожидаемых ошибок равно:

N = 23 × МИМi + 2 × ИМi .

Основные выводы, следующие из модели IBM, таковы:

количество ожидаемых ошибок в следующей версии может увеличиться по сравнению со старой версией, если будет изменено достаточно большое количество старых модулей (СИМ) и/или будет введено достаточно большое количество новых модулей (НМ). Поэтому перед выпуском такой версии понадобятся дополнительные усилия по ее тестированию;

введение новых модулей быстрее приводит к появлению ошибок, чем исправление старых модулей. Однако, если удастся вместо изменения большого числа старых модулей создать несколько новых с требуемой функциональностью, то это приведет к уменьшению оценки ожидаемых ошибок. То есть на некотором этапе усовершенствования ПО поддержка старых модулей является не эффективной, а более целесообразно с точки зрения надежности написать новые модули.

Модель Шумана

Рассмотрена в [16]. Предполагается, что Er – количество ошибок в начальный момент времени и в течение времени t устраняется ec(t) ошибок в расчете на одну команду. Тогда:

– количество оставшихся ошибок на одну команду, где IT – число машинных команд, которое предполагается постоянным.

Предполагается, что частота отказов z(t) пропорциональна числу ошибок, оставшихся в ПО, то есть z(t) = с · er(t).

Тогда вероятность безотказной работы на интервале времени (0, t):

.

Простая эвристическая модель двух независимых групп тестирования Руднера

Описана в [11] и [20]. В этой модели исключается основной недостаток модели Миллса. Здесь тестирование осуществляется двумя независимыми группами.

Пусть есть две независимые группы тестирования.

N1 и N2 – число ошибок, обнаруженных каждой группой соответственно. N12 – число одинаковых ошибок, обнаруженных обеими группами (т.е. число ошибок обнаруженных дважды), N – число всех ошибок программы (см. рис. 74).

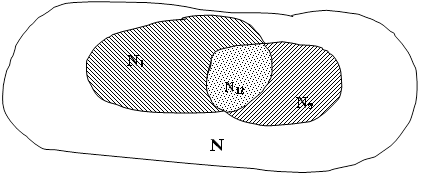
Рисунок A.3 – Область ошибок программы

Эффективность тестирования каждой из групп представим как

E1 = N1/N, E2=N2/N.

Предположим, что вероятность обнаружения всех ошибок каждой группой одинакова (это следует из того, что у каждой группы были одинаковые условия и одинакова квалификация их составов). Тогда можно рассматривать каждое подмножество пространства N как аппроксимацию всего пространства, т.е. если 1–я группа обнаружила 10% всех ошибок, то она должна была найти примерно 10% всякого случайным образом выбранного подмножества, например, подмножества N2. Тогда (N1/N) » (N12/N2) и (N2/N) » (N12/N1). Тогда получаем:

N = (N1 ·N2)/ N12.(А.24)

Например, две группы нашли 20 и 30 ошибок соответственно. Из них – 10 ошибок общие. Имеем согласно формуле (А.24) общее число ошибок N = 60 и из них не обнаружено 60 – 20 – 30 + 10 = 20 ошибок.

Линейная модель

В работе [16] предлагается описывать количество ошибок в программе как линейную функцию от сложности программы, то есть

где zi – показатели сложности ПО такие как:

количество ветвлений;

количество циклов;

количество вычислений;

число комментариев;

количество вызовов функций и т.п.;

ai – весовые коэффициенты.

Методом регрессионного анализа (МНК) по данным об ошибках пяти различных проектов показано, что наибольший вклад в N вносят общее число ветвлений z4 и общее число логических операторов z6 и, что N = 0,0454 · z4 + 0,254· z6; со стандартной ошибкой – 54,4 и доверительным интервалом – 0,982.

В работе [5] рассмотрены модели количества ошибок, основанные на знании объема исходных текстов ПО. Данные модели не учитывают квалификацию программиста и подобные трудно измеримые факторы. В этих моделях используются коэффициенты пропорциональности, которые нужно искать из опытных данных не совсем ясными методами.

Похожие работы

Экономическая деятельность и ее информационное обеспечение

Скачать

249681

5

8

... . Становление рыночной экономики в России породило ряд проблем. Одной из таких проблем является обеспечение безопасности бизнеса. На фоне высокого уровня криминализации общества, проблема безопасности любых видов экономической деятельности становится особенно актуальной. Информационная безопасность среди других составных частей экономической безопасности (финансовой, интеллектуальной, кадровой, ...

Разработка системы реального времени в виде планировщика исполнения заданий

Скачать

104513

2

0

... ресурсов компьютера между пользователями и задачами (система разделения времени) будет создана программная разработка планировщика задач, в котором главной целью является успеть среагировать на происходящие события в жестко заданный интервал времени (система реального времени). На основе планировщика будет реализован протокол, требующий поддержки реального времени. Для проектирования его ...

Разработка и исследование имитационной модели локальных вычислительных сетей

Скачать

141641

20

15

... на лазерные компакт-диски. Система моделирования Орлан ориентирована на достаточно широкий круг пользователей. В первую очередь, естественно, это администраторы вычислительных сетей предприятий, стоящие перед задачей проектирования или исследования сети. Обязательное условие, накладываемое системой – проектируемая сеть должны основываться на стандарте Ethernet. Но, так как абсолютное ...

Автоматизированная информационная система Учет экономической деятельности мукомольного цеха

Скачать

176646

13

0

... без применения компьютерной техники. Непрекращающееся развитие любого предприятия, учреждения или организации, а как следствие объёмов и сложности информации требует расширения компьютерных сетей и автоматизированных информационных систем. Но кроме очевидных выгод компьютерная техника несет в себе опасность здоровью и поэтому актуальной становится проблема охраны труда человека в процессе работы ...