Навигация
Модель для случая l ¹ const
2.3.4 Модель для случая l ¹ const
Итак, процесс работы клиент–серверного ПО зависит от количества исправленных в ней до этого ошибок. То есть от интенсивности потоков событий, переводящих элемент из состояния в состояние, зависят от того сколько элементов было в системе в данном состоянии. Чем большее количество раз ПО было на доработке (исправление ошибок в нем), тем меньше поток ошибок в будущем. Считаем, что ошибки исправляются корректно, то есть при исправлении не вносятся новые ошибки или вносятся, но гораздо реже, чем исправляются. При этом уменьшается интенсивность потока событий, переводящий каждый элемент (модуль или поток или процесс) ПО из состояния «исправен» (работоспособен) в состояние «неисправен».
Предложенный подход позволяет построить достоверную модель численности состояний ПО, исходя из этого предположения. Итак, пусть система S состоит из большого числа N однородных элементов (модулей или потоков одного модуля), каждый из которых может быть в одном из двух состояний:
x1 – работоспособен (работает);
x2 – не рабочий (обнаружена ошибка и исправляется).
На каждый модуль действует поток ошибок с интенсивностью l, которая зависит от количества исправленных ранее в модуле ошибок. Каждый неисправный элемент исправляется в среднем со скоростью m в единицу времени. В начальный момент (t = 0) все элементы (модули) исправны. Все потоки событий – пуассоновские (может быть с переменной интенсивностью). Напишем уравнения динамики средних для средних численностей состояний. Граф состояний одного модуля имеет вид, представленный на рисунке:

Рисунок 14 – Граф состояния модуля
Здесь l` – интенсивность потока ошибок в зависимости от предыдущих исправлений.
Найдем l` от числа предыдущих исправлений этого модуля. Выскажем предположение, что l` уменьшается с количеством исправленных ошибок до некоторого постоянного значения нечувствительности к исправлениям (например, когда количество исправленных ошибок становится равным количеству вносимых ошибок, или количество ошибок в модуле становится столь малым, что они начинают срабатывать с постоянной интенсивностью) по экспоненциальному закону и стремиться к некоторому минимуму тем быстрее, чем быстрее исправляются ошибки m – как показано на рис.15.
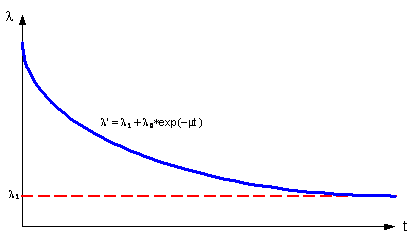
Рисунок 15 – Интенсивность потока ошибок
Для упрощения предположим, что l` обратно пропорционально m(m) числу модернизаций модуля, то есть убывает по гиперболическому закону:
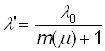 .(14)
.(14)
На основе графа (см. рис. 14) дифференциальные состояния динамики средних запишутся в виде:
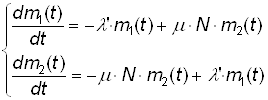 (15)
(15)
где m1(t), m2(t) – средние численности состояний x1 и x2.
Из этих двух уравнений можно выбрать одно, например, второе, а первое отбросить. Во второе уравнение подставим выражение для m1(t) из условия:
m1(t) + m2(t) = N.
Тогда получим вместо системы уравнений (15) одно дифференциальное уравнение:
![]()
Из предположения (14) имеем:
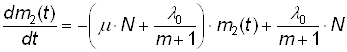 (16)
(16)
При этом количество модернизаций m зависит от интенсивности исправления модуля m и количества программистов (или групп программистов) P работающих над исправлением модулей. Предположим, что:
m(m) = m×P×t(17)
Окончательно получим уравнение для m2(t):
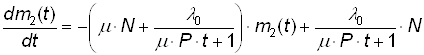 (18)
(18)
Решать это уравнение нужно при начальном условии m2(t=0) = 0 численными методами.
2.4 Разработка обобщенной модели надежности ПО типа клиент–сервер
Рассмотрим теперь уравнения смешанного типа. До сих пор мы описывали процессы, протекающие в ПО, либо с помощью уравнений для вероятностей состояний, либо с помощью уравнений динамики средних, где неизвестными функциями являются средние численности состояний. Уравнения первого типа применяются тогда, когда ПО сравнительно простое и его состояния сравнительно немногочисленны. Уравнения второго типа специально предназначены для описания процессов, происходящих в ПО, состоящего из многочисленных модулей. Для таких систем нам удалось найти не вероятности состояний, а средние численности состояний.
На практике чаще встречаются ситуации смешанного типа. Для такого ПО и напишем уравнения. Эта модель применима для ПО, которое состоит из элементов–модулей разного типа: немногочисленных (уникальных) (например, в архитектуре клиент–сервер это – сервер) и многочисленных (в архитектуре клиент–сервер это – клиенты), причем состояния тех и других взаимообусловлены.
В этом случае для модулей первого типа можно составить дифференциальные уравнения, в которых неизвестными функциями являются вероятности состояний. Для модулей же второго типа – средние численности состояний. Такие уравнения будем называть уравнениями смешанного типа.
Рассмотрим ПО S, состоящее из большого количества N одинаковых клиентских программ и одного сервера, который координирует работу всех клиентских программ. Как сервер, так и отдельные клиенты могут отказывать (зависать). Интенсивность потока отказов сервера зависит от числа x работающих программ–клиентов (то есть фактически зависит от интенсивности входных данных и их диапазона):
![]() (19)
(19)
Интенсивность потока неисправностей каждого модуля–клиента при работающем сервере равна l` (см. (14)).
Среднее время устранения ошибки в сервере, учитывая сложность сервера, больше чем среднее время устранения ошибки в клиенте:
![]() ,(20)
,(20)
где m0 – скорость устранения ошибок в клиенте (скорость исправления ошибки программистом), S – коэффициент сложности сервера.
Опишем процесс, протекающий в ПО, с помощью уравнений смешанного типа, в которых неизвестными функциями будут:
вероятности состояний сервера;
средние численности состояний клиентов.
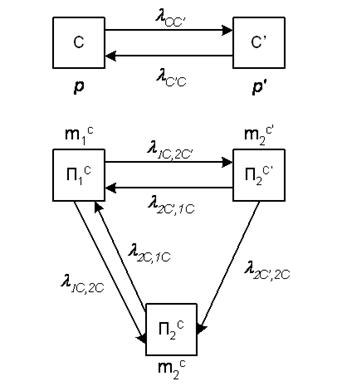
Рисунок 16 – Граф смешанной системы
Опишем нашу систему при помощи графа, показанного на рис.16. Этот граф распадается на два подграфа. Первый (верхний) – это подграф состояний сервера, который может быть в одном из двух состояний:
C(t) – работает;
С’(t) – не работает (ошибка обнаружена и исправляется).
Что же касается программы–клиента, то для нее мы учитываем возможность находиться в одном из трех состояний:
П1С(t) – клиент работает при работающем сервере;
П2С(t) – клиент не работает при работающем сервере;
П2С’(t) – клиент не работает при не работающем сервере;
Состояние сервера характеризуется в момент времени t одним из событий C(t) и C’(t). Вероятности этих событий обозначим через p(t) и p’(t) = 1 – p(t), а численности состояний П1С(t), П2С(t) и П2С’(t) соответственно: X1С(t), X2С(t) и X2С’(t).
Соответствующие математические ожидания обозначим как:
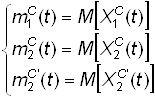 (21)
(21)
Очевидно, для любого момента времени t:
![]() (22)
(22)
где N – число клиентов, работающих с сервером.
Определим интенсивности потоков событий для графа (см. рис. 16). Прежде всего, по условию задачи (19):
![]() (23)
(23)
Из (20) следует:
 (24)
(24)
Далее, программа–клиент переходит из состояния П1С(t) в состояние П2С’(t) не сама по себе, а только вместе и одновременно с сервером (когда тот зависает). Поэтому:
![]() (25)
(25)
Аналогично:
![]() (26)
(26)
Для остальных переходов не трудно установить соответствующие интенсивности, если учесть тот факт, что второй (нижний) подграф отличается от рассмотренного ранее (см. рис. 14) только наличием еще одного состояния П2С’, когда клиентская программа простаивает на время исправления ошибки в программе–сервере. С учетом этого имеем:
![]() (27)
(27)
![]() (28)
(28)
![]() (29)
(29)
Напишем для графа (см. рис. 16) дифференциальные уравнения смешанного типа, приближенно описывающие нашу систему (аргумент t для краткости записи опущен):
 (30)
(30)
где:
![]()
![]()
Отметим, что, положив в (30) все левые части равными 0, можно найти решение для стационарного режима, а он существует, так как система эргодическая.
Заметим, что из этой системы уравнений можно исключить два уравнения: одно из первых двух, пользуясь уравнением p + p’ = 1, и одно – из последующих трех, пользуясь соотношением нормировки (22).
Эти уравнения решаются при условии, что в начале сервер и все программы–клиенты работают: t = 0; p = 1; p’ = 0; ![]() ;
; ![]() (31)
(31)
В случае, если важно исследовать, скажем, как быстро система восстанавливается при выходе из строя сервера, то начальные условия нужно выбрать другими: t = 0; p = 0; p’ = 1; ![]() ;
; ![]() ,
, ![]() (32)
(32)
3. Экспериментальная часть
3.1 Обоснование выбранного метода реализации
Основной проблемой нахождения надежности ПО при помощи моделей надежности является необходимость знать начальное количество ошибок в ПО. Эту величину определить достаточно трудно (практически не возможно).
Поэтому одним из преимуществ предлагаемой модели по сравнению с другими является то, что в ней не используется предположение о начальном количестве ошибок N0 в ПО. Вместо нее используются достаточно просто измеряемые характеристики ПО, такие как интенсивность появления ошибок и интенсивность устранения ошибок. Хотя предложенная модель надежности и не использует эту величину, тем не менее, можно воспользоваться ее результатами для нахождения начального количества ошибок в программе N0 методом обратного расчета. Это позволит найти такие характеристики надежности ПО, как время наработки до отказа, его вероятность и время достижения нужной надежности при заданных начальных условиях.
Похожие работы
... . Становление рыночной экономики в России породило ряд проблем. Одной из таких проблем является обеспечение безопасности бизнеса. На фоне высокого уровня криминализации общества, проблема безопасности любых видов экономической деятельности становится особенно актуальной. Информационная безопасность среди других составных частей экономической безопасности (финансовой, интеллектуальной, кадровой, ...
... ресурсов компьютера между пользователями и задачами (система разделения времени) будет создана программная разработка планировщика задач, в котором главной целью является успеть среагировать на происходящие события в жестко заданный интервал времени (система реального времени). На основе планировщика будет реализован протокол, требующий поддержки реального времени. Для проектирования его ...
... на лазерные компакт-диски. Система моделирования Орлан ориентирована на достаточно широкий круг пользователей. В первую очередь, естественно, это администраторы вычислительных сетей предприятий, стоящие перед задачей проектирования или исследования сети. Обязательное условие, накладываемое системой – проектируемая сеть должны основываться на стандарте Ethernet. Но, так как абсолютное ...
... без применения компьютерной техники. Непрекращающееся развитие любого предприятия, учреждения или организации, а как следствие объёмов и сложности информации требует расширения компьютерных сетей и автоматизированных информационных систем. Но кроме очевидных выгод компьютерная техника несет в себе опасность здоровью и поэтому актуальной становится проблема охраны труда человека в процессе работы ...
0 комментариев