Влияние интенсивности обращений клиентов к серверу

3.3.4 Влияние интенсивности обращений клиентов к серверу

Увеличение интенсивности обращения каждого клиента к серверу не дает ожидаемого эффекта, т.к. каждый клиент обычно работает в своей узкой части ОД и выбивает ошибки из этой части, при этом значительная ОД остается не проверенной, а значит с ошибками. Проведем розыгрыш при увеличении интенсивности обращений с 500 до 2500 в сутки (рис.23).

Начальные условия розыгрыша:

K (кол-во программ-клиентов) = 10;

P (кол-во программистов) = 3;

a (ширина запроса клиента) = 0,00001;

N0 (начальное количество ошибок) = 250;

s (сложность сервера) = 2;

Dt (шаг итерации) = 0,0004 (сутки);

lобр (интенсивность потока обращений клиента к серверу) = 2500/сутки;

lиспр (интенсивность потока исправления ошибки) = 1/сутки;

pвнес (вероятность внесения ошибки при исправлении) = 0,1/сутки

M (количество итераций) = 250000;

Общее время розыгрыша: 100 (сутки);

К (число розыгрышей) =10

 

3.3.5 Определение начального количества ошибок в ПО

Данная модель в сочетание с предложенной марковской моделью надежности ПО позволяет оценить количество ошибок в программе следующим образом – получить расчетный результат, а затем подобрать начальное количество ошибок в ПО таким образом, чтобы результаты розыгрыша совпадали с результатом расчета.

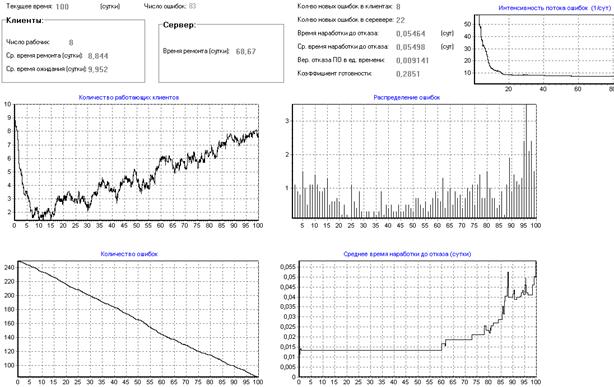
Рисунок 23 – Влияние интенсивности обращений клиентов к серверу

Для решения этой задачи с помощью программы моделирования необходимо добиться того, чтобы начальная интенсивность потока ошибок l0 из модели надежности ПО типа клиент–сервер совпадала с начальной интенсивностью потока ошибок в программе моделирования. Напрямую это сделать невозможно, так как в программе моделирования такого параметра нет. Для этого в программе моделирования нужно положить a = 0.5, то есть каждое обращение клиента к серверу и ответ сервера к клиенту должен с вероятностью 1 порождать ошибку. Затем необходимо добиться того, чтобы количество обращений за сутки клиентов к серверу (т.е. K*lобр) было равно l0. Остальные начальные параметры программы моделирования необходимо положить равными аналогичным параметрам модели надежности.

Найдем начальное количество ошибок для примера рассмотренного ранее. Для того чтобы начальная интенсивность потока ошибок в программе моделирования была равна l0=10, положим a = 0.5, а lобр при 3–х программистах положим равной 3,3. Итак:

Начальные условия розыгрыша:

K (кол-во программ-клиентов) = 10;

P (кол-во программистов) = 3;

a (ширина запроса клиента) = 0,5;

N0 (начальное количество ошибок) = 9;

s (сложность сервера) = 3;

Dt (шаг итерации) = 0,0001 (сутки);

lобр (интенсивность потока обращений клиента к серверу) = 3,3/сутки;

lиспр (интенсивность потока исправления ошибки) = 0,5/сутки;

pвнес (вероятность внесения ошибки при исправлении) = 0/сутки

M (количество итераций) = 100000;

Общее время розыгрыша: 10 (сутки);

К (число розыгрышей) =50

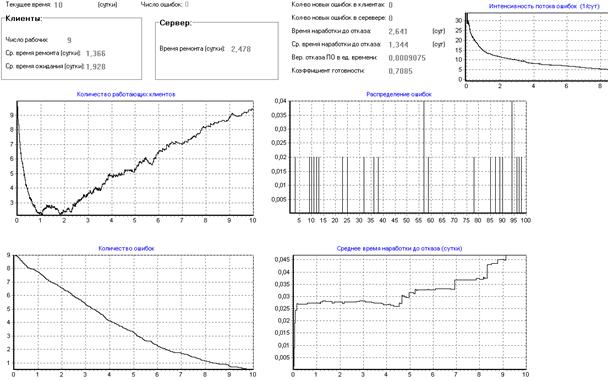
Рисунок 24 – Определение начального количества ошибок в ПО

Как видно из рис.24, при начальном количестве ошибок в программе равном 9 получили результат аналогичный полученному в модели, то есть клиенты начнут устойчиво работать на 4 сутки. Число 9 было получено методом подбора различных начальных значений количества Er ошибок в программе на начальный момент времени.

Таким образом, комбинируя модель и розыгрыш можно вычислить первоначальное количество ошибок в ПО и другие его характеристики.

 

3.3.6 Поиск начального количества ошибок в программе по начальной и конечной интенсивностям отказов

Наша модель позволяет решать обратную задачу, т. е. зная количество программистов, интенсивность их работы и интенсивность отказов в начале опытной эксплуатации и в конце опытной эксплуатации можно подобрать начальное количество ошибок в программе, совпадающее с ними.

Проведем такое исследование для периода опытной эксплуатации ПО и исследуем возможность передачи системы в промышленную эксплуатацию [25]. Известно, что ее обслуживает 3 программиста. Количество программ–клиентов – 10. Интенсивность отказов в начале опытной эксплуатации была 1 отказ в сутки. Через пол года работы получили интенсивность отказов – 1 отказ в месяц или 0,033 отказа в сутки. При этом объем одного запроса вычислим как отношение объема одного запроса к размеру всей базы данных. Он равен: a = 0,01Кб/10000Кб = 0,000001. Попробуем методом подбора найти первоначальное количество ошибок такое, чтобы оно удовлетворяло начальным и конечным условиям задачи. С учетом того, что каждую минуту одна из программ–клиентов получает данные, получаем интенсивность обращения к серверу – 1500 обращений в сутки.

Розыгрыш показывает, что таким начальным и конечным условиям соответствует ПО с 20–25 ошибками в начале работы и 10–14 ошибок на 180 сутки и коэффициент готовности 0,9. Для розыгрыша:

Начальные условия розыгрыша:

K (кол-во программ-клиентов) = 10;

P (кол-во программистов) = 3;

a (ширина запроса клиента) = 0,000001;

N0 (начальное количество ошибок) = 25;

s (сложность сервера) = 2;

Dt (шаг итерации) = 0,0005 (сутки);

lобр (интенсивность потока обращений клиента к серверу) = 1500/сутки;

lиспр (интенсивность потока исправления ошибки) = 2/сутки;

pвнес (вероятность внесения ошибки при исправлении) = 0,1/сутки

M (количество итераций) = 360000;

Общее время розыгрыша: 180 (сутки);

К (число розыгрышей) =5

Был получен результат (рис.25).

Рисунок 25 – Поиск начального количества ошибок

Из полученных данных видно, что после 180 дней опытной эксплуатации в системе останется примерно 5 ошибок и коэффициент готовности будет более 0.95, а среднее время наработки на отказ будет более 20 суток. Это приемлемые значения для надежности такой системы и следовательно ее можно передавать в промышленную эксплуатацию.

Моделирование следующих 180 дней промышленной эксплуатации показывают, что за это время будет обнаружено и исправлено всего 3, 4 ошибки, а коэффициент готовности достигнет 0.99 и среднее время наработки до отказа будет около 60 дней (рис.26).

Рисунок 26 – Поиск начального количества ошибок

Для сравнения проведем розыгрыш для количества ошибок, равном 100 и неизменных остальных начальных условиях (рис.27).

Рисунок 27 – Поиск начального количества ошибок

Из полученных результатов видно, что к концу опытной эксплуатации программы с таким начальным количеством ошибок через 180 дней еще останется около 25 ошибок, коэффициент готовности – 0.9, а среднее время наработки до отказа – около 6 суток, что говорит о низкой надежности ПО, вследствие чего программа не готова к передаче в промышленную эксплуатацию и необходимо продлить ее опытную эксплуатацию еще на полгода.

Выводы

В ходе выполнения дипломной работы были изучены существующие модели надежности ПО и методы разработки качественного (прежде всего надежного, Кг > 0,999) ПО в условиях ограниченных ресурсов. На основе проведенного аналитического обзора современного состояния дел было выяснено, что на данный момент отсутствует общее решение проблемы надежности ПО, а есть множество частных решений, которые не учитывают такие существенные факторы, как интенсивность внесения и устранения ошибок в программе, время разработки ПО. Кроме того, влияние объема и сложности текста программ на надежность ПО в настоящее время непрерывно уменьшается. Таким образом, ни одну из существующих моделей нельзя считать достаточной для оценки надежности ПО малого и среднего объема (до 100 тысяч строк) из–за неопределенности их входных параметров, таких как начальное количество ошибок в ПО, количество ветвлений, циклов и т.п.

В ходе выполнения работы была создана новая математическая модель надежности ПО на основе марковских систем массового обслуживания, позволяющая проводить расчет характеристик надежности ПО.

Предлагаемая модель является более простой по отношению к рассмотренным. Основным ее преимуществом является отсутствие в ней начального количества ошибок в ПО.

Основным практическим результатом работы является программа для прогнозирования поведения надежности ПО со временем, основанная на методе Монте–Карло и предложенной модели надежности ПО. Сочетание двух подходов – марковской модели надежности ПО и прогнозирования при помощи метода Монте–Карло – позволяет более точно и более всесторонне оценить характеристики надежности ПО. Работа модели показана на конкретных примерах. Полученные результаты хорошо согласуются с результатами, полученными на практике.

Таким образом, созданная программа моделирования позволяет, задавая различные начальные условия, наблюдать поведение надежности ПО во времени. Это позволяет использовать ее для решения оптимизационных задач (например, поиска оптимальных ресурсов для достижения заданного уровня надежности, оптимальной интенсивности тестирования при заданных характеристиках клиент–сервера и количестве программистов). В частности, это позволяет найти начальное количество ошибок в ПО.

Таким образом, модель и программу моделирования можно рекомендовать использовать при разработке и сопровождении ПО, когда уровень надежности должен быть высоким, а достигнуть и подтвердить его не просто.

 

Список использованных источников

1.         А.В. Антонов, А.С. Степанянц. Методы анализа надежности (безошибочности) программного обеспечения программно-технических средств //Труды ІІ Междунар. конф. "Идентификация систем и задачи управления" (SICPRO-2003). – С.924-942.

2.         Ханджян А.О. Анализ современного состояния разработки надежного программного обеспечения //Естественные и технические науки. – М., 2005. – №2. – С. 220 – 227.

3.         Лисс В.А. Математические модели надежности программного обеспечения распределенных систем //Известия СПбГТУ "ЛЭТИ". Сер. "Информатика, управление и компьютерные технологии". – 2005. – Вып.2. – С.26-32.

4.         В.Г. Промыслов, А.В. Антонов, С.И. Масолкин, А.С. Степанянц. Оценка надежности программного обеспечения на различных этапах жизненного цикла сложных программ // Труды V Междунар. конф. "Идентификация систем и задачи управления" (SICPRO-2006). – С.1300-1304.

5.         Шураков В. В. Надежность программного обеспечения систем обработки данных: Учебник.— 2–е изд., перераб. и доп.— М.: Финансы и статистика, 1987.—272 с.: ил.

6.         ГОСТ Р ИСО/МЭК 9126–93. Информационная технология. Оценка программной продукции. Характеристики качества и руководства по их применению. – 12 с.

7.         ГОСТ 28195–89. Оценка качества программных средств. Общие положения. – М.: Госком. СССР по стандартам – 38 с.

8.         Соммервилл И. Инженерия программного обеспечения. – М.: Вильямс, 2002. – 624 с.

9.         Larson D., Miller K. Silver Bullets for Little Monsters: Making Software More Trustworthy, IEEE IT Pro, March/April 2005 (русская версия: Ларсон Д., Миллер К. Серебряные пули для маленьких монстров //Открытые системы №5–6, 2005 С.20 – 23)

10.       ISO/IEC 91261:1998. Информационная технология. – Характеристики и метрики качества программного обеспечения. – Часть 1: Характеристики и подхарактеристики качества.

11.       Майерс Г. Надежность программного обеспечения. – М.: Мир, 1980. – 360 с.

12.       Гаспер Б.С. Надежность функционирования автоматизированных систем. – Пермь: ПГТУ, 1999. – 70 с.

13.       Иыуду К.А. Надежность, контроль и диагностика вычислительных машин и систем. – М.: Высшая школа, 1989. – 320 с.

14.       Липаев В.В. Функциональная безопасность программных средств. – М.: СИНТЕГ, 2004. – 340 с.

15.       Vincent J., Waters A., Sinclair J. Software quality assurance. Vol II. A programmer guide. – Englewood Cliff, New Yersey: Prentice–Hall. – 1988. – 192 p.

16.       Тейер Т., Липов М., Нельсон Э. Надежность ПО. – М.: Мир, 1981. – 328 с.

17.       Международный стандарт. МЭК 60880–2. Программное обеспечение компьютеров в системах важных для безопасности атомных электростанций. – IEC. М.: 2002. – 90 с.

18.       Кулаков А.Ф. Оценка качества программы ЭВМ. – К.: Техника, 1984. – 168 с.

19.       Липаев В.В. Надежность программных средств. – М.: СИНТЕГ, 1998. – 232 с.

20.       Полонников Р.И., Никандров А.В. Методы оценки надежности программного обеспечения. – СПб: Политехника, 1992. – 80 с.

21.       Штрик А.А., Осовецкий Л.Г., Мессих И.Г. Структурное проектирование надежных программ встроенных ЭВМ. – Л.: Машиностроение, 1989. – 296 с.

22.       Вентцель Е.С. Исследование операций. – М.: Сов. Радио, 1972. – 552 с.

23.       Гаспер Б.С. Надежность функционирования автоматизированных систем. – Пермь: ПГТУ, 1999. – 70 с.

24.       Куракин А.Л. Фактор надежности в оптимизации аппаратуры для научных исследований //Технологии приборостроения №1(5) (СНИИП) – 2003. – С. 62‑65.

25.       Ханджян А.О. Моделирование надежности программного обеспечения. - http://www.software-testing.ru/lib/handzhyan/software_quality_modeling.htm

 

Приложение А. Примеры моделей надежности ПО

 

Экспоненциальная модель роста надежности Джелински, Моранда, Шумана

Это одна из самых распространенных на сегодняшний день моделей надежности ПО опирается на теорию надежности аппаратуры [11, 13, 16, 19, 20, 21, 23].

Один из способов оценки СВМО – наблюдение за поведением программы в течение некоторого периода времени и нанесение на график значений между последовательными ошибками. На рис. А.1 изображено увеличение надежности ПО (кривые R1, R2, R3 – функции надежности, т. е. вероятность того, что ни одна ошибка в программе не произойдет или не будет обнаружена на временном интервале [0…t]) при исправлении в нем ошибок.

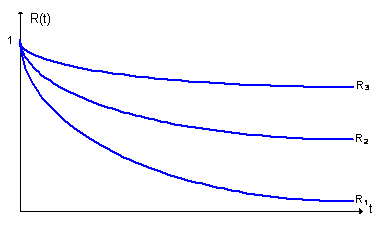
Рисунок A.1 – Увеличение надежности ПО при исправление в нем ошибок

Для разработки модели вводят следующие предположения:

li = Z(t) постоянно до обнаружения и исправления ошибки или интенсивность обнаружения ошибок;

li = Z(t) = K · ( N – i ) – т.е. Z(t) прямо пропорционально числу оставшихся ошибок, где N – неизвестное первоначальное число ошибок, i – число обнаруженных ошибок, K – некоторая неизвестная константа. Эта зависимость отображена на рис.А.2.

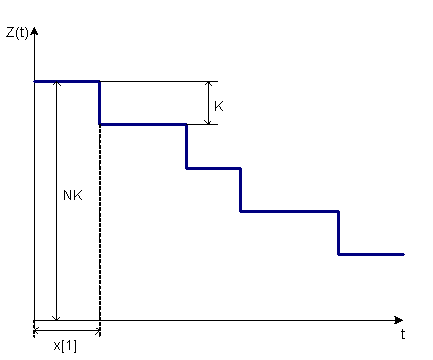
Рисунок A.2 – Функция риска

При обнаружении и исправлении ошибки функция риска уменьшается на K.

Неизвестные N и K можно оценить, если некоторое количество ошибок уже обнаружено. Предположим, что обнаружено n ошибок, а x[1], x[2], …, x[n] – интервалы времени между этими ошибками. Тогда, в предположении что Z(t) постоянно между ошибками, плотность вероятности для x[i] будет равна

p( x[i] ) = K · ( N – i ) · exp{ –K · ( N – i ) · x[i] }.

Значение N даст основной результат – оценку полного числа ошибок. Знание K позволяет использовать уравнение для предсказания времени до появления (n+1)‑й ошибки и последующих ошибок.

Это частный случай модели Шумана. Предположим, что интервалы времени отладки между обнаружениями двух ошибок имеет экспоненциальную зависимость и частота ошибок пропорциональна числу еще необнаруженных ошибок. Таким образом, функция плотности распределения времени обнаружения i–ой ошибки, отсчитываемого от момента выявления (i–1)–ой ошибки имеет вид

,

где

и N – число первоначально присутствующих в ПО ошибок.

Эта модель построена на следующих допущениях:

время до следующего отказа распределено экспоненциально;

интенсивность отказов пропорционально оставшимся в ПО ошибкам.

Тогда вероятность безотказной работы ПО:

, (А.1)

где

li=CD * ( N0–(i–1) ), (А.2)

CD – коэффициент пропорциональности,

N0 – первоначальное число ошибок в ПО.

В (А.1) отчет времени начинается от момента последнего (i–1)–го отказа.

Если известны все моменты обнаружения ошибок ti и каждый раз в этот момент устраняется одна ошибка, то, используя метод максимального правдоподобия, можно получить уравнение для определения значения начального количества ошибок N0.

По методу максимального правдоподобия находим CD и N0. Функция правдоподобия имеет вид:

 .

Откуда получаем условия для нахождения экстремумов:

,

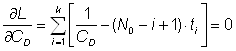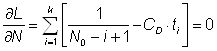
Отсюда получаем решение для CD и N0:

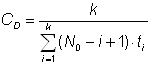,(А.3)

.(А.4)

Уравнение (А.4) решается методом перебора.

Пусть в ходе отладки зафиксированы интервалы времени между отказами ПО t1=10, t2=20, t3=25 ч. Определим по вышеприведенным формулам вероятность отсутствия 4–го отказа, начиная с момента устранения 3–го отказа.

Решаем (А.4) методом перебора и получаем N=4. Следовательно, из (А.3) имеем CD=0,02. Тогда из (А.1, А.2) получаем P(t4)=exp(0,02*t4) и, следовательно, l4=0,02 и среднее время до следующего отказа программы составляет <t4>=1/l4=50 ч.

Это одна из первых и простых моделей. Модель использована при разработке весьма ответственных проектов (например, для программы Apollo). В ее основу положены следующие допущения:

интенсивность обнаружения ошибки R(t) пропорциональна текущему числу ошибок в программе;

все ошибки равно вероятны и их появления независимы друг от друга;

время до следующего отказа распределено экспоненциально;

ошибки постоянно исправляются без внесения новых ошибок;

R(t) = const на интервале между двумя соседними ошибками;

В соответствии с этими допущениями функцию распределения (риска) интенсивности ошибок между (i–1) и i–ой ошибками можно представить как:

R(t) = K×[N0 – (i–1)],

где K – коэффициент пропорциональности; N0 – исходное число ошибок в ПО.

Все интервалы времени

Dti = ti – ti–1

имеют экспоненциальное распределение:

P(Dti) = exp{– K×[N0 – (i–1)] ×Dti }.

Из принципа максимального правдоподобия для K и N0 получают следующие оценки:

,(А.5)

.(А.6)

Нелинейное уравнение (А.6) достаточно сложно для решения численными методами, так как оно имеет локальные экстремумы и не всегда имеет решение.

Модель позволяет найти время до обнаружения следующей ошибки tn+1 и время необходимое для обнаружения всех ошибок T:

,

.

Можно посчитать Dn – количество ошибок, которое следует обнаружить и устранить для повышения наработки между обнаружениями ошибок от T1 до T2:

Dn = N0 · T0 · ( 1/T1 – 1/T2).(А.7)

Также можно получить затраты времени Dt на проведение тестирования, которые позволяют устранить Dn ошибок и соответственно повысить наработку от T1 до T2:

Dt = N0 · T0 · ln( T2 / T1 ) / K .(А.8)

Коэффициент готовности:

,

Коэффициент простоя КП = 1 – КГ, где t' – период проверок, t1 – время затрат ресурсов на проверки, tВ – длительность восстановления работоспособности программы.

Относительная длительность отладки в этой модели:

,

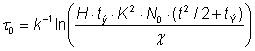где H – количество систем, в которых функционирует программа; tЭ – длительность эксплуатации программы; c ‑ коэффициент увеличения затрат ресурсов на единицу машинного времени.

Средняя наработка на отказ:

Тср = 1/l.

Следует подчеркнуть статистический характер приведенных соотношений.

Из (А.8) видно, что время, затрачиваемое на тестирование, пропорционально квадрату первоначального количества ошибок T0 в программе. Приведем пример: пусть N0 = 1000; T0 = 1 час. Требуется повысить надежность программы с T1 =1 час до T2 = 1 месяц = 720 часов. Тогда из (А.7) Dn = 999, что фактически означает, что нужно обнаружить все ошибки для получения устойчивой работы ПО в 1 месяц. И на это будет затрачено время Dt ~ 60 дней (при расчете K по формуле (А.5) было сделано предположение о неизменности , в этом случае

K=n*T0/(сумма ар. прогрессии)).

На практике же будет затрачено гораздо меньше времени и найдено гораздо меньше ошибок, так как предположение о равномерности использования всего текста программы в процессе эксплуатации не верно. И, скорее всего, будет за меньшее время обнаружено 99% ошибок в той части программы, которая исполняется чаще, чем другая. В малоэксплуатируемой части останется не обнаруженными до 99% ошибок. Отсюда следует вывод о большой важности точного подбора входных данных при тестировании как можно более соответствующих режиму эксплуатации и вывод о необходимости сокращать время тестирования за счет меньшего тестирования малоиспользуемых ветвей программы. При этом важно не забывать о различных режимах эксплуатации ПО: нормальном, аварийном, ждущем и т.п.

Постулат, что программа не меняется за исключением исправления ошибки, а новые ошибки не вносятся, является спорным. Желание выразить надежность ПО некоторой функцией времени вполне логично, однако в действительности она от времени не зависит. Надежность ПО является функцией числа ошибок, их серьезности и расположения, а также того, насколько интенсивно система используется (интенсивность входного потока данных).

Статистическая модель Миллса

Описана в [11] и [20]. Программа специально "засоряется" некоторым количеством заранее известных ошибок. Эти ошибки вносятся в программу случайным образом, а затем делается предположение, что для ее собственных и искусственно внесенных ошибок вероятность обнаружения при последующем тестировании одинакова и зависит только от их количества. Тестируя программу в течении некоторого времени и отсортировывая собственные и внесенные ошибки можно оценить N – первоначальное число ошибок в программе.

Пусть: S – число специально внесенных ошибок; n – число найденных собственных ошибок в программе; u – число найденных внесенных ошибок; n+u – количество обнаруженных ошибок при тестировании.

Тогда по методу максимального правдоподобия имеем: N = S · n / u.

Основное допущение модели – распределение «посеянных» ошибок совпадает с распределением по программе собственных ошибок, и, следовательно, обнаружение, как тех, так и других ошибок равновероятно – что является существенным недостатком этой модели.

При этом можно выдвигать и проверять гипотезы об N. Пусть в программе не более k собственных ошибок и внесли нее еще S ошибок. Теперь программа тестируется, пока не будут обнаружены все специально внесенные ошибки. Причем в этот момент подсчитывается число обнаруженных собственных ошибок (обозначим его, как и раньше, как n). Введем уровень значимости C:

(А.9)

С – мера доверия к модели, то есть мера правильности нашего предположения о количестве k собственных ошибок и дает оценку для количества ошибок

,

которое нужно внести в программу, чтобы проверить гипотезу с заданным уровнем значимости.

Например, если мы утверждаем, что в программе нет ошибок (k = 0), и внося в программу 4 ошибки, все их обнаруживаем, не встретив ни одной собственной ошибки, то C = 0.80. А чтобы достичь уровня 95 %, надо было бы внести в программу 19 ошибок.

Этот метод не очень эффективен в случае применения его в реальной практике, так как если предположить что в программе своих ошибок n = 1000 (что более реально, чем n = 0), то для достижения уровня правдоподобия 0,95 в программу придется ввести 19019 ошибок, что само по себе уже тяжелая задача.

Формулу (А.9) можно модифицировать так, чтобы устранить недостаток, заключающийся в том, что C нельзя предсказать до тех пор, пока не будут обнаружены все искусственно внесенные ошибки (а это может и не произойти за ограниченное время, отведенное на тестирование). Модифицированной формулой можно пользоваться уже после того, как найдено j внесенных ошибок:

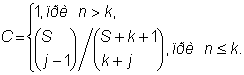(А.10)

Это математически очень простая и интуитивно понятная модель. Процесс внесения ошибок – само слабое звено модели, так как должны вноситься "типичные" для данной программы ошибки (то есть искусственно внесенные ошибки должны иметь то же распределение вероятности, что и собственные ошибки). Кроме того, эта модель не учитывает системных ошибок, то есть ошибок вносимых на этапе проектирования, а не самого кодирования.

Модель Бейзина

Пусть ПО содержит Nk команд [20]. Случайным образом из них выбирается n команд, в которые вводятся ошибки. Затем для тестирования случайным образом выбирается r команд. Если в ходе тестирования будет обнаружено n собственных и m привнесенных («посеянных») ошибок, то полное число N0 ошибок содержащихся в программе перед началом тестирования (следует из метода максимального правдоподобия) можно определить как:

.

Простая экспоненциальная модель

В отличие от модели Джелинского–Моранды R(t) ¹ const [20].

Пусть N(t) – число обнаруженных к моменту времени t ошибок и пусть функция риска пропорциональна числу оставшихся к моменту t в программе ошибок: R(t) = K×(N(0) – N(t)).

Продифференцируем обе части этого уравнения по времени:

.

Учитывая, что dN(t)/dt есть R(t) (число ошибок, обнаруженных в единицу времени), получим дифференциальное уравнение:

с начальными условиями N(0) = 0, R(0) = K×N0.

Решением этого уравнения является функция:

R(t) = K×N0×exp(–K×t).(А.11)

Для K и N0 получают следующие оценки (с применением МНК) для первых n ошибок:

,

,

где

.

Используя (А.11) можно определить время необходимое для снижения интенсивности появления ошибок с R1(t) до R2(t):

.

Дискретная модель Шика–Уолвертона

Эта модель рассмотрена в работах [12, 20, 21]. Применяется при следующих допущениях:

предполагается, что частота проявления ошибок (интенсивность отказов) линейно зависит от времени испытаний ti между моментами обнаружения последовательных i–й и (i–1)–й ошибок;

появление ошибок равновероятно и независимо;

ошибки корректируются без введения новых.

Тогда:

,

где k – коэффициент пропорциональности, обеспечивающий равенство единице площади под кривой вероятности обнаружения ошибок.

В этом случае для оценки вероятности безотказной работы получается выражение, соответствующее распределению Релея:

,

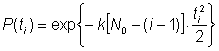где P(ti) = P(T³ti).

Отсюда плотность распределения времени наработки на отказ:

.

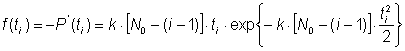Использовав функцию максимального правдоподобия, получим оценку для N0 и K:

, .

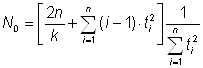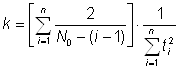Модель Вейбулла

В [12] и [20] приводится модель надежности ПО с учетом ступенчатого характера изменения надежности при устранении очередной ошибки.

Функция риска для этой модели представляется в виде: R(t) = (a/b) ×(t/b)a–1, где a > 0, и b > 0 – константы модели; t – интервал времени безошибочной работы.

Если a > 1, то интенсивность обнаружения ошибок растет со временем, если a < 1, то – падает.

Плотность распределения вероятности до появления очередной ошибки описывается распределением Вейбулла:

.

Наработка до отказа выражается через гамма–функцию:

,

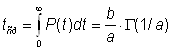где P(t) – вероятность безотказной работы и P(t) = 1 – Q(t), где Q(t) – вероятность отказа:

.

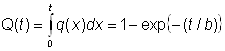Для оценки параметров a и b используются следующие формулы:

,

где

b = exp{–b0/a},

,

k – число интервалов тестирования,

,

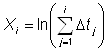Dtj – длина j–го интервала тестирования,

,

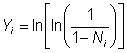Ni – нормированное суммарное число ошибок, обнаруженных к моменту ti.

Определение надежности по результатам тестирования

Рассмотрены в работе [13]. Оценку надежности ПО при стохастическом (когда входные данные выбираются согласно своим функциям распределения и основным статистическим моментам) функциональном тестировании целесообразно производить на основании заключительной серии стохастических тестов (например, при приемочных испытаниях), когда отказы программы отсутствуют. Тогда для оценки вероятности безотказной работы программы может быть использована формула (оценка безошибочности ПО производится таким же методом как оценка безотказности аппаратуры):

,(А.12)

где pн – нижняя доверительная граница вероятности безотказной работы ПО при однократном прохождении набора стохастических входных данных; gн – доверительная вероятность; n – число проходов при тестировании.

Пусть, например, n=150 прохождений со случайными исходными данными. Исходы всех тестов положительные (ошибок не обнаружено), т.е. количество отказов ПО равно нулю. Необходимо определить нижнюю доверительную границу вероятности безотказной работы ПО при одном прохождении, при gн = 0,9.

Согласно (А.11) имеем pн = 0.985.

Сделанное выше допущение относительно независимости результатов отдельных тестов программы не вполне обосновано, так как наличие ошибки в ПО обнаруживается скорей всего, большим количеством тестов, чем это можно ожидать, исходя из независимости их результатов. Поэтому представляет интерес другой подход, где ПО рассматривается как сообщение, состоящее из N символов. Пусть каждый стохастический тест проверяет в среднем r символов из N и пусть один из N элементов содержит ошибку.

Пусть вероятность того, что при одном тесте ошибка не будет обнаружена, оценивается как 1 – r/N. Вероятность того, что при n независимых тестах ошибка не будет обнаружена, равна (1 – r/N)n. Если ошибочных символов в ПО больше чем один, то вероятность их обнаружения одним тестом будет еще больше, так как эта оценка является оценкой снизу.

Пусть n = 150; r/N = 0,3. Тогда вероятность обнаружения ошибки в ПО

p = 1 – (1 – r/N)150 = 1 – 1,72×10–20 @ 1.

Настолько высокая оценка вероятности обнаружения ошибок получается благодаря тому, что в соответствии с данной моделью каждый символ программы проверяется в среднем многократно, и вероятность того, что некоторый символ ни в одном тесте не проверяется, весьма мала.

Модель избыточности

Можно попробовать использовать подход, предложенный в статье [24] для описания эффективности защиты ПО от сбоев посредством введения в нее избыточного кода. Эффективность защиты (в расчете на которую в ПО вводится избыточный код, который снижает функциональные характеристики ПО, в частности, быстродействие и требует больших ресурсов (например, для использования образцового в этом отношении языка JAVA нужно как минимум 128 Мб ОЗУ)), априорно определим как вероятность P (являющейся функцией времени T периодичности работы программного модуля) нужности (срабатывания) защиты. Эта вероятность в рассматриваемом случае может быть выражена произведением вида:

P = Pe * Pr * Pd,(А.13)

где Pe – вероятность того, что сбой произойдет (например, закончатся ресурсы оперативной памяти и не будет выделена память);

Pr – вероятность того, что защита от этого сбоя сработает;

Pd – вероятность того, что сообщение о сбое будет получено и обработано (т.е. что диагностика сработает).

По сути данной задачи речь идет о двух типах случайных событий: