Аналитический обзор литературы
Выводы
Содержательная постановка задачи
Разработка модели надежности ПО типа клиент–сервер
Модель с заменой вероятностей состояний на средние численности состояний
Модель для случая l ¹ const
Алгоритм функционирования программы
Практические результаты моделирования
Влияние интенсивности обращений клиентов к серверу
Событии (нежелательном) состоящем в том, что произошел прогнозируемый сбой;
Навигация
Модель с заменой вероятностей состояний на средние численности состояний
Разработка программно–алгоритмических средств для определения надёжности программного обеспечения на основании моделирования работы системы типа "клиент–сервер"
104437
знаков
5
таблиц
35
изображений
2.3.2 Модель с заменой вероятностей состояний на средние численности состояний
Пусть программа S состоит из N одинаковых модулей (или потоков) и граф состояния каждого модуля представлен на рисунке:
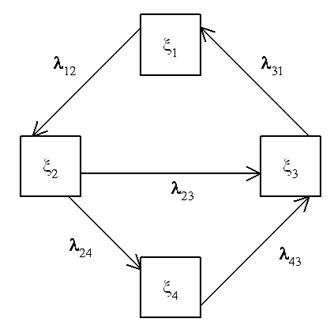
Рисунок 10 –Граф состояний модуля
В начальный момент времени t = 0 все модули находятся в состоянии x1.
Непосредственно по графу (см. рис. 10) составляем уравнения Колмогорова для вероятностей состояния;
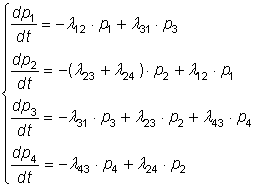(5)
Умножим левую и правую части каждого из уравнений (5) на число модулей N и введем в левых частях N под знак производной, а также учтем (3), тогда:
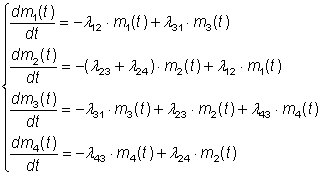(6)
В системе уравнений (6) (которые называются уравнениями динамики средних) неизвестными функциями являются уже непосредственно средние численности состояний (точнее математические ожидания численности состояний). Как видно, эти уравнения составлены по тому же правилу, что и уравнения для вероятностей состояний. Поэтому их можно было составить сразу, минуя промежуточный этап.
Очевидно, что для каждого момента времени t средние численности состояний удовлетворяют нормировочному условию:
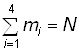(7)
И поэтому одно (любое) из уравнений системы (6) можно отбросить. Отбросим, например, третье уравнение из (6), а в остальные уравнения вместо m3 подставим выражение согласно (7):
.
Тогда окончательно получим:
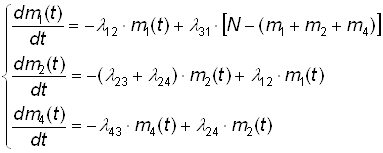(8)
Эту систему нужно решать при начальном условии: t = 0; m1 = N; m2=m3=m4=0.
Решение такой системы дифференциальных уравнений (а для стационарного режима – системы алгебраических уравнений) легко провести на ЭВМ методом численного интегрирования.
Предположим, что это осуществлено и нами получены четыре функции m1(t), m2(t), m3(t) и m4(t). Найдем дисперсии численностей состояний D1(t), …, D4(t).
Из (3) и (4) следует:
,
где k = 1, … – число состояний модуля(9)
Зная математические ожидания и дисперсии численности состояний, мы получаем возможность оценить и вероятности различных состояний системы в целом, то есть вероятность того, что численность какого–то состояния будет заключена в определенных пределах. Действительно, так как число модулей N в программной системе велико, то по закону больших чисел можно полагать, что численность k–го состояния приближенно распределено по нормальному закону. И, следовательно, вероятность того, что случайная величина Xk (численность k–го состояния) будет заключена в границах от a до b, будет выражаться формулой:
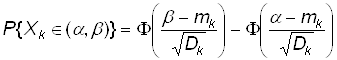, где F(x) – функция Лапласа.
2.3.3 Модель для случая N модулей–клиентов
Распространим модель на наиболее часто встречающийся на практике случай, когда каждый модуль–клиент находится в одном из двух состояний: рабочем или нерабочем.о в нерабочем состоянии.
Пусть к серверу может обращаться N клиентов, порождающих N потоков. Каждый поток может находиться в одном из двух состояний:
x1 – рабочий;
x2 – не рабочий (обнаружена ошибка).
Переход модуля из состояния x1 в состояние x2 происходит под действием потока данных (запросов) с интенсивностью l; среднее время восстановления (обнаружения и исправления ошибки в модуле) модуля равно
.
Составим уравнения динамики средних и решим их при условии, что в начальный момент все модули находятся в рабочем состоянии.
Граф состояний каждого модуля имеет вид, показанный на рисунке:
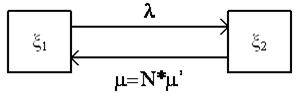
Рисунок 11 – Граф состояния модуля
где: m = N×m’ так как при исправлении ошибки в одном модуле, ошибка мгновенно исправляется во всех остальных модулях тоже;
m1(t) – среднее число функционирующих модулей в момент времени t;
m2(t) – среднее число не функционирующих программных модулей (потоков) в момент времени t.
Уравнение динамики средних будет:
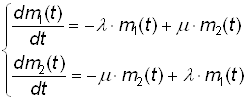(10)
И начальное условие m1(0) = N при t = 0.
Учтем, что для любого момента времени t выполняется нормировочное условие, из которого следует что:
(11)
Подставляя (1) в первое уравнение из (10), получим:
Решением этого уравнения будет:
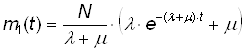(12)
Из (11) и (12) находим m2(t):
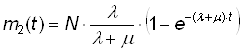(13)
При t ® ¥ имеем стационарный режим:
;
.
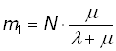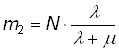Построим на графике функции m1(t) и m2(t).
Для случая программной системы с большим количеством программ N, m будет всегда больше l. Это означает, что среднее количество работающих модулей m1 всегда будет больше среднего числа неработающих модулей m2. Причем в этом случае m = N×m’ и при N ®¥:
, 
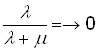
Отсюда можно сделать вывод, что чем больше пользователей системы (и чем больше количество потоков N), тем она надежнее или тем быстрее станет надежной.
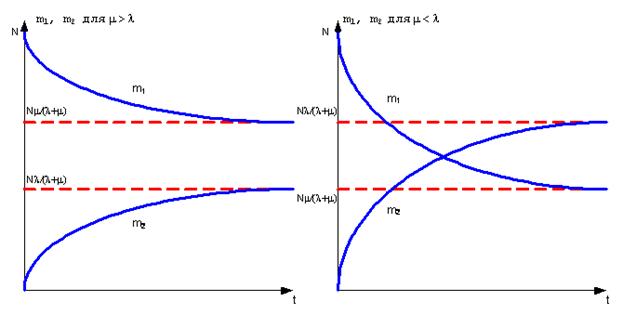
Рисунок 12 – Графики m1(t) и m2(t)
Определим дисперсию численностей состояний из (9):
Очевидно, что дисперсии численности первого и второго состояния будут одинаковыми: D(t) = D2(t) = D1(t).
При t ® ¥
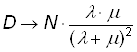
График функции D(t) изображен на рисунке:
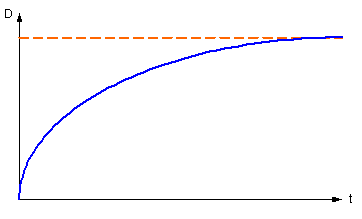
Рисунок 13 – График D
Например, в стационарном состоянии для N=200, l = 2 запроса/сутки и 
суток получим следующие значения:
– число работающих модулей.
Вообще говоря, для полноты картины в модели нужно учесть, что интенсивность потока ошибок l ¹ const, и уменьшается со временем, так как количество ошибок в программе уменьшается на единицу с интенсивностью m и стремиться к некоторому постоянному уровню. Например,
Вообще, если быть более строгим в рассуждениях, то мы имеем дело фактически с одним объектом, который после каждого исправления становится новым объектом с новым количеством ошибок (не обязательно меньшим) и это говорит о том, что в данной системе нет отсутствия последействия, то есть процесс не пуассоновский, а, следователь:но, и не марковский. Поэтому, вообще говоря, нужно брать процесс Эрланга второй степени и применять метод приведения процесса к марковскому (метод псевдосостояний), описанный в [11]. Этот метод в работе не рассматривается из–за его сравнительной сложности и из–за того, что этим эффектом можно пренебречь при большом количестве состояний клиентов и/или большом количестве программ–клиентов, а также учитывая то предположение, что новый объект (новая программа) появляется мгновенно после исправления в ней ошибки.
Похожие работы
... . Становление рыночной экономики в России породило ряд проблем. Одной из таких проблем является обеспечение безопасности бизнеса. На фоне высокого уровня криминализации общества, проблема безопасности любых видов экономической деятельности становится особенно актуальной. Информационная безопасность среди других составных частей экономической безопасности (финансовой, интеллектуальной, кадровой, ...
... ресурсов компьютера между пользователями и задачами (система разделения времени) будет создана программная разработка планировщика задач, в котором главной целью является успеть среагировать на происходящие события в жестко заданный интервал времени (система реального времени). На основе планировщика будет реализован протокол, требующий поддержки реального времени. Для проектирования его ...
... на лазерные компакт-диски. Система моделирования Орлан ориентирована на достаточно широкий круг пользователей. В первую очередь, естественно, это администраторы вычислительных сетей предприятий, стоящие перед задачей проектирования или исследования сети. Обязательное условие, накладываемое системой – проектируемая сеть должны основываться на стандарте Ethernet. Но, так как абсолютное ...
... без применения компьютерной техники. Непрекращающееся развитие любого предприятия, учреждения или организации, а как следствие объёмов и сложности информации требует расширения компьютерных сетей и автоматизированных информационных систем. Но кроме очевидных выгод компьютерная техника несет в себе опасность здоровью и поэтому актуальной становится проблема охраны труда человека в процессе работы ...
0 комментариев