АНАЛИЗ ЧУВСТВИТЕЛЬНОСТИ ОПТИМАЛЬНОГО РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

4. АНАЛИЗ ЧУВСТВИТЕЛЬНОСТИ ОПТИМАЛЬНОГО РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

  4.1. Теоретическое введение

Неизбежное колебание значений таких экономических параметров, как цены на продукцию и сырье, запасы сырья, спрос на рынке и т.д. может привести к неоптимальности или непригодности прежнего режима работы. Для учета подобных ситуаций проводится анализ чувствительности, т.е. анализ того, как возможные изменения параметров исходной модели повлияют на полученное ранее оптимальное решение задачи ЛП.

Для решения задач анализа чувствительности ограничения линейной модели классифицируются следующим образом. Связывающие ограничения проходят через оптимальную точку. Несвязывающие ограничения не проходят через оптимальную точку. Аналогично ресурс, представляемый связывающим ограничением, называют дефицитным, а ресурс, представляемый несвязывающим ограничением – недефицитным. Ограничение называют избыточным в том случае, если его исключение не влияет на ОДР и, следовательно, на оптимальное решение. Выделяют следующие три задачи анализа на чувствительность.

1. Анализ сокращения или увеличения ресурсов:

·          на сколько можно увеличить (ограничения типа ) запас дефицитного ресурса для улучшения оптимального значения ЦФ?

·          на сколько можно уменьшить (ограничения типа ) запас недефицитного ресурса при сохранении оптимального значения ЦФ?

2. Увеличение (ограничения типа ) запаса какого из ресурсов наиболее выгодно?

3. Анализ изменения коэффициентов ЦФ: каков диапазон изменения коэффициентов ЦФ, при котором не меняется оптимальное решение?

4.2. Методика графического анализа чувствительности оптимального решения.

4.2.1. Первая задача анализа на чувствительность (анализ на чувствительность к правой части ограничений)

Проанализируем чувствительность оптимального решения задачи о производстве радиоприемников. ОДР задачи (рис.3.1) – многоугольник ABCDE. В оптимальной точке D пересекаются прямые (1) и (2). Поэтому ограничения (1) и (2) являются связывающими, а соответствующие им ресурсы (суточный объем элементов электронных схем и производительность первой технологической линии) – дефицитными.

Рассмотрим экономический смысл этих понятий. Точка максимума ЦФ D соответствует суточному производству 60 шт радиоприемников первой модели и 5 шт радиоприемников второй модели. В производстве радиоприемников используются однотипные элементы электронных схем. Суточный запас на складе этих элементов – это правая часть связывающего ограничения (1) (950 шт/сутки). Согласно этому ограничению, на производство в точке D расходуется

 [шт элементов/сутки](1).

Аналогично видим, что производительность первой технологической линии - это правая часть связывающего ограничения (2) (60 шт/сутки). Согласно этому ограничению в точке D данная линия производит 60 радиоприемников первой модели в сутки.

 Таким образом, понятие "связывающие ограничения" (1) и (2) означает, что при производстве радиоприемников в точке D(60;5) запасы элементов электронных схем расходуются полностью, а так же производительность первой технологической линии используется в полном объеме. По этой причине невозможно дальнейшее наращивание производства. В этом заключается экономический смысл понятия дефицитности ресурсов, т.е. если предприятие сможет увеличить суточные запасы элементов электронных схем или производительность первой технологической линии, то это позволит увеличить выпуск радиоприемников. В связи с этим возникает вопрос: до какого уровня целесообразно увеличить данные ресурсы, и на сколько при этом увеличится оптимальное производство радиоприемников?

Правило №1

Чтобы графически определить максимальное увеличение запаса дефицитного ресурса, вызывающее улучшение оптимального решения,

необходимо передвигать соответствующую прямую в направлении улучшения ЦФ до тех пор, пока это ограничение не станет избыточным.

При прохождении прямой (1) через точку К (рис.4.1) многоугольник ABKE становится ОДР, а ограничение (1) – избыточным. Действительно, если удалить прямую (1), проходящую через точку К, то ОДР ABKE не изменится. Точка К становится оптимальной, в этой точке ограничения (2) и (3) становятся связывающими.

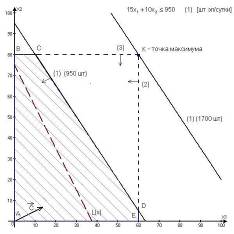
Рис.4.1. Анализ увеличения суточного запаса элементов электронных схем

Правило №2

Чтобы численно определить максимальную величину запаса дефицитного ресурса, вызывающую улучшение оптимального решения,

необходимо:

 1) определить координаты точки , в которой соответствующее ограничение становится избыточным;

2) подставить координаты  в левую часть соответствующего ограничения.

Координаты точки К(60;80) находятся путем решения системы уравнений прямых (2) и (3). Т.е. в этой точке предприятие будет производить 60 шт радиоприемников первой модели и 80 шт радиоприемников второй модели. Подставим  и  в левую часть ограничения (1) и получим максимально допустимый запас элементов электронных схем

 [шт эл/сутки].

Дальнейшее увеличение запаса элементов электронных схем нецелесообразно, потому что это не изменит ОДР и не приведет к другому оптимальному решению (см. рис.4.1). Доход от продажи радиоприемников в объеме, соответствующем точке К, можно рассчитать, подставив ее координаты в выражение ЦФ

 [$/сутки].

Рассмотрим вопрос о целесообразности увеличения производительности первой технологической линии. Согласно правилу №1, соответствующее ограничение (2) становится избыточным в точке J, в которой пересекаются прямая (1) и ось переменной (рис.4.2). Многоугольник ABCJ становится ОДР, а точка J(63,33;0) (или (63;0)-целочисленное решение) – оптимальным решением.

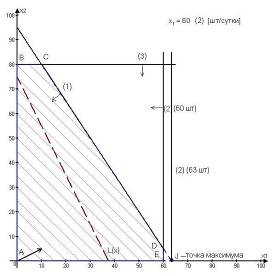
Рис.4.2. Анализ увеличения производительности первой технологической линии

В точке J выгодно производить только радиоприемники первой модели (63 шт в сутки). Доход от продажи при этом составит

 [$/сутки]

Чтобы обеспечить такой режим работы, согласно правилу №2, производительность первой технологической линии надо увеличить до величины

  [шт/сутки].

Ограничение (3) является несвязывающим, т.к. не проходит через оптимальную точку D (см. рис.4.3). Соответствующий ему ресурс (производительность второй технологической линии) является недефицитным. С экономической точки зрения это означает, что в данный момент уровень производительности второй технологической линии непосредственно не определяет объемы производства. Поэтому некоторое его колебание может никак не повлиять на оптимальный режим производства в точке D.

Например, увеличение (уменьшение) суточного объема второй технологической линии будет соответствовать перемещению прямой ограничения  (3) вверх (вниз). Перемещение прямой (3) вверх никак не может изменить точку D максимума ЦФ. Перемещение же прямой (3) вниз не влияет на существующее оптимальное решение только до пересечения с точкой D (см. ниже правило №3). Из рис.4.3 видно, что дальнейшее перемещение (3) приведет к тому, что точка D будет за пределами новой ОДР, выделенной более темным цветом. Кроме того, любое оптимальное решение для этой новой ОДР будет хуже точки D.

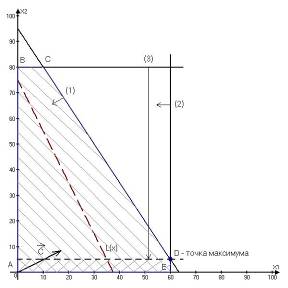
Рис.4.3. Анализ уменьшения производительности второй технологической линии

Правило №3

Чтобы определить максимальное уменьшение запаса недефицитного ресурса, не меняющее оптимальное решение,

необходимо передвигать соответствующую прямую до пересечения с оптимальной точкой.

Правило №4

Чтобы численно определить минимальную величину запаса недефицитного ресурса, не меняющую оптимальное решение,

необходимо подставить координаты оптимальной точки в левую часть соответствующего ограничения.

Чтобы выяснить, до каких пределов уменьшение производительности второй технологической линии не повлияет на производство в точке D, используем правило №4 Подставляем в левую часть ограничения (3) координаты точки D, получаем

[шт/сутки].

Делаем вывод: предельный уровень, до которого может уменьшиться объем второй технологической линии, и при котором не изменится оптимальность полученного ранее решения, равен 5 шт радиоприемников в сутки.

Результаты решения первой задачи анализа оптимального решения на чувствительность представлены в табл.4.1.

Таблица 4.1

№	Тип ресурса	Max изменение ресурса, , шт/сутки	Max изменение дохода, ,  $/сутки	Ценность дополнительной единицы ресурса , $/шт
(1)	Дефицитный	1700-950=+750	4000-2500=+1500
(2)	Дефицитный	63-60=+3	2520-2500=+20
(3)	Недефицитный	5-80=-75	2500-2500=0

4.2.2. Вторая задача анализа на чувствительность (увеличение запаса какого из ресурсов наиболее выгодно)

Анализ табл.4.1 показывает, что к улучшению оптимального решения, т.е. к увеличению суточного дохода приводит увеличение дефицитных ресурсов. Для определения выгодности увеличения этих ресурсов используют понятие ценности дополнительной единицы i-го ресурса

где – максимальное приращение оптимального значения ЦФ;  – максимально допустимый прирост объема i-го ресурса.

Например, из табл.4.1 следует, что увеличение суточного запаса элементов электронных схем (ограничение (1)) на 1 шт позволит получить дополнительный доход, равный 2 $/сутки, в то время как увеличение производительности первой технологической линии (ограничение (2)) на 1 шт принесет 6,7 $/сутки. Недефицитные ресурсы имеют нулевые ценности, поскольку изменение этих ресурсов не приводит к увеличению дохода.

Вывод: дополнительные вложения в первую очередь необходимо направлять на увеличение суточного объема первой технологической линии, а лишь потом на увеличение суточного запаса элементов электронных схем. Изменять недефицитные ресурсы нет необходимости.